2 章末复习（3课时）课件+教案

这是一份2 章末复习（3课时）课件+教案，文件包含小结与复习课件pptx、复习练习pptx、综合与实践课件pptx、章末复习教案doc等4份课件配套教学资源，其中PPT共67页， 欢迎下载使用。
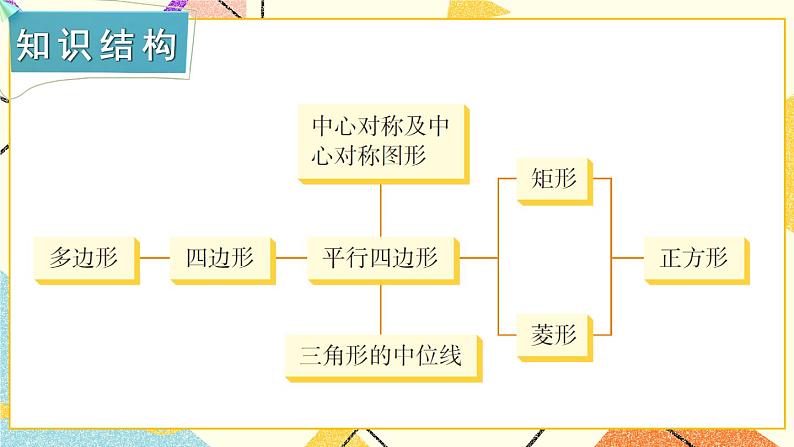
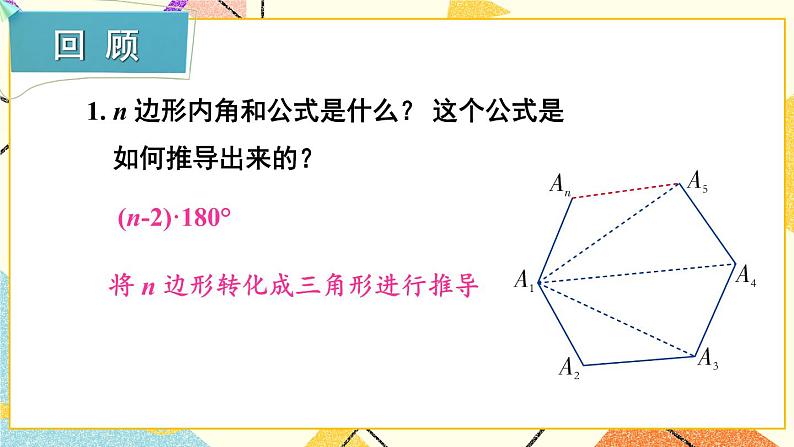
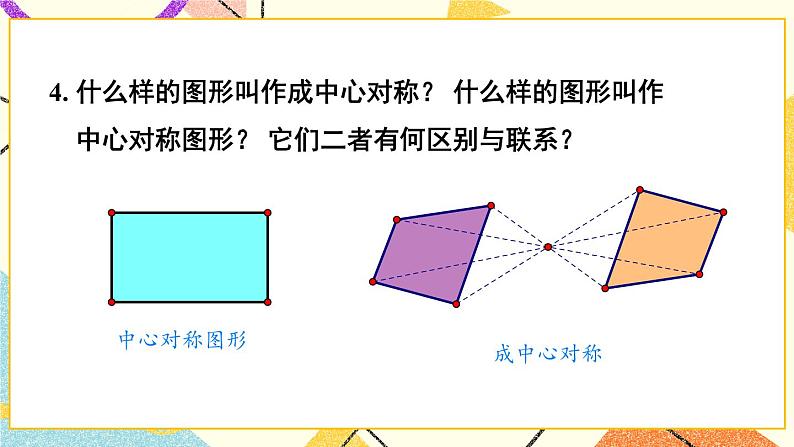
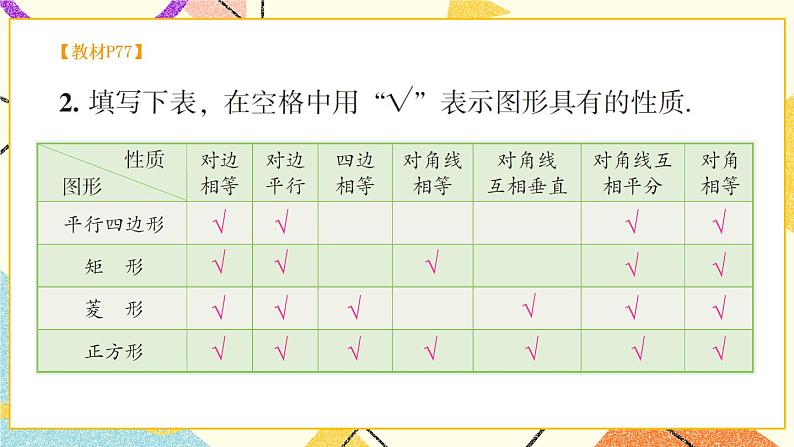
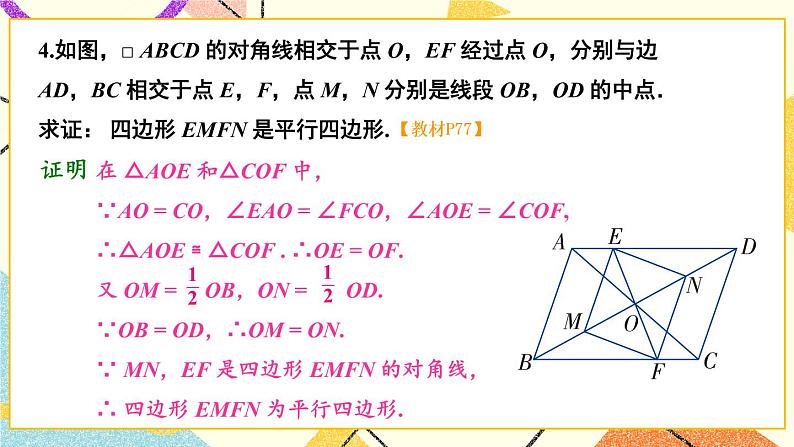
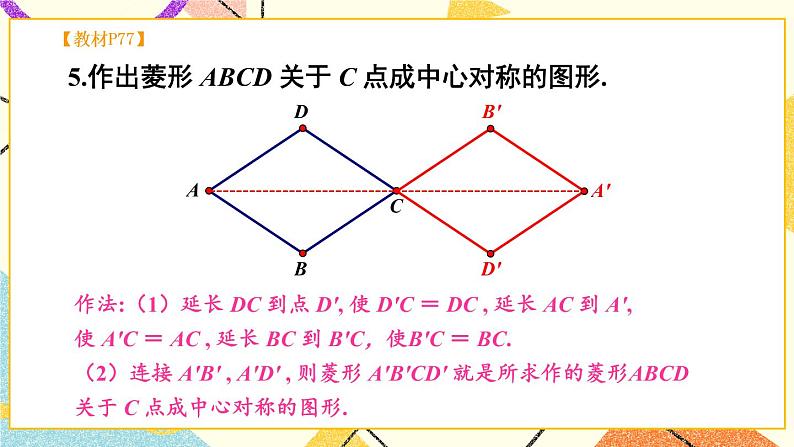
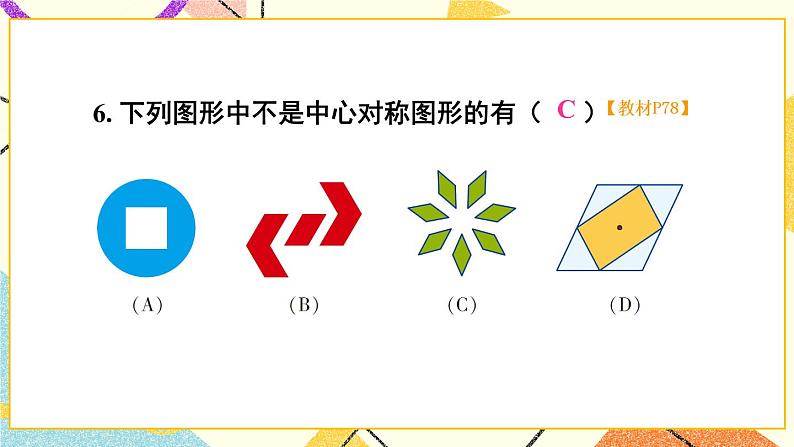
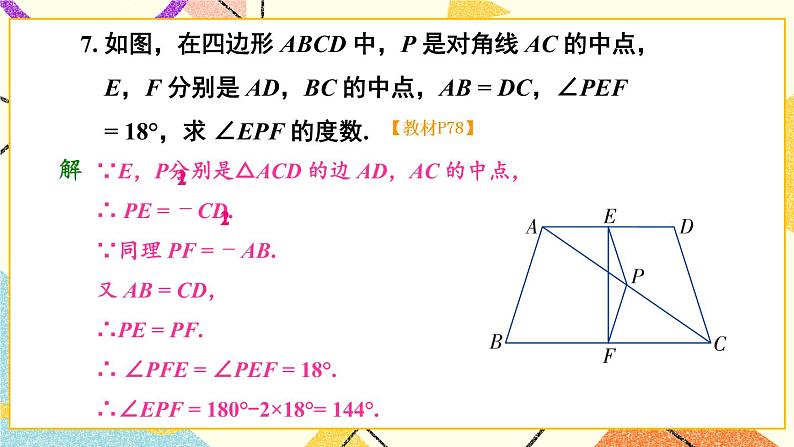
章末复习【知识与技能】1.理解四边形、平行四边形、矩形、菱形、正方形的有关概念；掌握平行四边形、矩形、菱形、正方形的有关性质和常用判别方法.2.能灵活运用特殊四边形的知识解决一些实际问题.【过程与方法】经历探究四边形、平行四边形、矩形、菱形、正方形之间的联系与区别的过程，类比掌握平行四边形、矩形、菱形、正方形的性质与常用的判别方法.【情感态度】在回顾与思考的过程中，让学生进一步领会特殊与一般的关系，逐渐理解类比、转化等一些重要的数学思想.【教学重点】建立知识结构，掌握特殊四边形之间的联系与区别.【教学难点】灵活运用所学知识解决有关问题.一、知识框图，整体把握二、释疑解惑，加深理解1.多边形的边数与内角和、外角和由于多边形的外角和等于360°是一个固定的值，求多边形的边数和内角和往往可以从外角和入手，使计算更简便.2.平行四边形和特殊平行四边形的性质与判定特殊平行四边形都具有平行四边形的性质，并且有它本身独有的性质与判定，学习过程中注意不能相互混淆.3.中心对称与中心对称图形成中心对称是对两个图形来说的，它表示两个图形之间的对称关系，中心对称图形是对一个图形说的，它表示某个图形的特征.三、典例精析，复习新知例1  一个多边形的某一个外角与所有内角的总和为1350°，求边数n和这个外角的度数.【分析】本题重点检验多边形的内角和是180°的整数倍的理解应用能力，注意到每一个外角都大于0°小于180°，可得不等式求解.【解答】由多边形的任一个外角都大于0°小于180°，则有1350°-180°<(n-2)·180°<1350°，解得812<n<912.因为n为整数，所以n=9，这个外角的度数为1350°-（9-2）·18°=90°.例2  如图，△ABC中，D在AB上，E在AC的延长线上，BD=CE，连结DE，交BC于F，∠BAC外角的平分线交BC的延长线于G，且AG∥DE，求证：BF=CF. 【分析】过点C作CM∥AB交DE于点M，可以证明BD=CM，然后再利用平行四边形的性质得到BF=CF.证明：过点C作CM∥AB交DE于点M，连结BM、CD，则∠CME=∠ADE，∵AG∥DE,∴∠EAG=∠E=∠ADM.又∵AB∥CM,∴∠ADM=∠CME,∴∠CME=∠CEM,∴CM=CE=BD.∵BDCM,∴四边形BMCD为平行四边形，∴BF=CF.例3  在矩形ABCD中，AB=2AD，E是CD上一点，且AE=AB，则∠CBE的度数是（    ）A.30°     B.22.5°     C.15°    D.以上答案都不对【分析】因为AE=AB=2AD，所以∠AED=30°，可求出∠EAB=30°，△AEB为等腰三角形，∠CBE=90°-∠EBA.解：∵四边形ABCD为矩形，∴AB∥CD，∠D=∠CBA=90°，∴∠AED=∠BAE，∵AB=2AD，AE=AB，∴AE=2AD，∠AED=30°，∴∠BAE=30°，∴∠ABE==75°，∴∠CBE=90°-∠ABE=90°-75°=15°.例4  如图，有一矩形纸片ABCD，AB=6cm，BC=8cm，将纸片沿EF折叠，使点B与D重合，求折痕EF的长.【分析】本题利用矩形性质，勾股定理及面积公式，显然折痕在BD的垂直平分线上，不难证得四边形BFDE为菱形，只要求ED的长问题就容易解决.解：连BD，BE，DF，由折叠的实际意义可知EF⊥BD，且EF平分BD，∴BE=ED，BF=FD，∵矩形ABCD，∴AB=CD，AD=BC，∠C=90°，AD∥BC，∴∠EDO=∠FBO，又∵BO=DO，∠BOF=∠DOF，∴△BOF≌△DOE，∴ED=BF，∴ED=BF=FD=BE，∴四边形BFDE为菱形，∴菱形BFDE的面积=×BD×EF=BF×CD，设BF=x=DF则FC=8-x，依题意有：x2=(8-x)2+62，解得x=，又BD2=BC2+CD2=82+62，BD=10,∴×10×EF=×6，∴EF=.例5  如图（1）在正方形ABCD的BC、CD边上取E、F两点，使∠EAF=45°，AG⊥EF于G，求证：AG=AB.【分析】欲证AG=AB，就图形直观来看，应证Rt△ABE与Rt△AGE全等，但条件不够，∠EAF=45°怎么用呢？显然∠1+∠2=45°，若把它们拼在一起，问题就解决了.证明：把△AFD绕点A旋转90°至△AHB（或延长EB至H使BH=DF），如图（2）.∵∠EAF=45°，∴∠1+∠2=45°，∵∠2=∠3，∴∠1+∠3=45°，又由旋转所得AH=AF，AE=AE，∴△AEF≌△AEH（SAS），∴AG=AB.【教学说明】典型例题的分析，对于学生解题有着重要的指导作用，特别是开阔了学生的眼界，拓展了学生的解题思路和方法.教师在讲评的过程中，要让学生明确本章的重点和难点，容易出错或忽略的地方重点强调，逐步提高.四、复习训练，巩固提高1.一个正多边形的每个外角都等于36°，那么它是      边形.2.在□ABCD中，对角线AC=12cm，BD=8cm，交点为O，若△AOB与△BOC的周长和为37cm，则□ABCD的周长为       cm.3.下列图形是中心对称图形而不是轴对称图形的是（      ）4.如果三角形的两边分别为3和5，那么连接这个三角形三边中点所得的三角形的周长可能是（     ）A.5.5       B.5      C.4.5       D.45.如图所示，在ABCD中，已知AD=10cm，AB=4cm，AE平分∠BAD交BC于点E，则EC等于（      ）A.7cm         B.6cmC.5cm         D.4cm6.如图，在正方形ABCD中，点E、F分别在BC和CD上，AE=AF.（1）求证：BE=DF；（2）连接AC交EF于点O，延长OC至点M，使OM=OA，连接EM、FM，判断四边形AEMF是什么特殊四边形？并证明你的结论.【教学说明】这部分安排了本章几个重点知识的运用，目的是为了检测学生的掌握情况，有利于及时发现错误，并有针对性查漏补缺.【答案】1.十    2.34    3.A    4.A    5.B6.（1）证Rt△ABE≌Rt△ADF,得BE=DF.（2）四边形AEMF是菱形，证明：∵四这形ABCD是正方形，∴∠BCA=∠DCA=45°，BC=DC，∵BE=DF，∴BC-BE=DC-DF，即CE=CF，∴△EOC≌△FOC，∴OE=OF，∵OM=OA，∴四边形AEMF是平行四边形，∵AE=AF，∴平行四边形AEMF是菱形.五、师生互动，课堂小结你能完整地回顾本章所学的四边形、平行四边形、特殊的平行四边形的有关知识吗？你认为哪些内容是大家需要掌握的？学习过程中还有哪些困惑？请与同学们共同交流探讨.【教学说明】通过师生共同回顾本章所学知识，让学生自主讨论、交流形成共识，易错的地方作必要的强调补充.1.布置作业：从复习题中选取.2.完成练习册.本节课从整理本章主要内容入手，用精选的例题为范本，让学生运用所学知识解决问题，并且通过训练使所学内容全面得到强化，能力逐步提高.第3章图形与坐标