






还剩14页未读,
继续阅读
所属成套资源:人教a版数学必修第一册课件PPT+同步练习整套
成套系列资料,整套一键下载
- 第四章 -4.3对数(课件PPT) 课件 13 次下载
- 第四章 -4.4对数函数(课件PPT) 课件 14 次下载
- 第五章 -5.1.1任意角(课件PPT) 课件 12 次下载
- 第五章 -5.1.2弧度制(课件PPT) 课件 12 次下载
- 第五章 -5.2.1三角函数的概念(课件PPT) 课件 19 次下载
第四章 -4.5函数的应用(二)(课件PPT)
展开
这是一份第四章 -4.5函数的应用(二)(课件PPT),共22页。
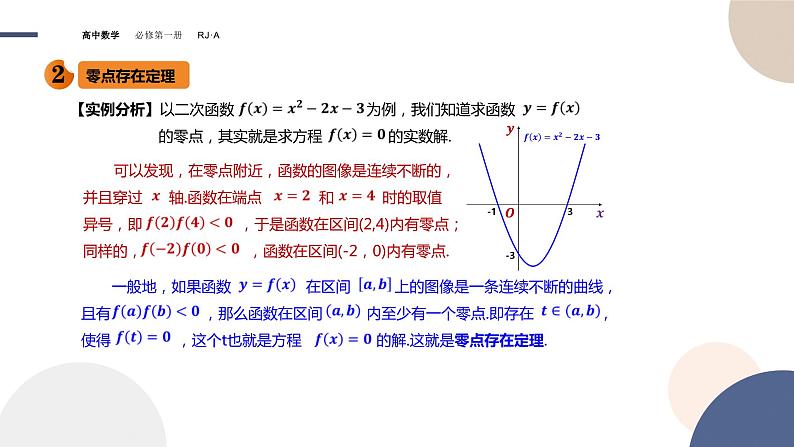
4.5函数的应用(二)第四章4.5.1 函数的零点与方程的解4.5.2用二分法求方程的近似解学习目标1.了解函数零点的定义.2.了解函数的零点与函数对应方程的根的关系.3.能够根据函数零点的判定方法判断函数零点所在的区间.4.了解二分法求方程近似解的原理,能借助计算器用二分法求函数零点的近似值.5.根据具体函数的图象,能够用二分法求相应方程的近似值.核心素养:数学抽象、逻辑推理、数学运算新知学习函数的零点与方程的解【导学】如何求二次方程 的实数根? 【答】由根的判别式 得: 对于一个一般的函数,也可以这么算吗?它们有什么异同点?函数的零点与方程的解【函数零点的定义】与二次函数的零点一样,对于一般函数 ,我们把使得 的实数 叫做函数 的零点. 这样,函数 的零点就是方程 的实数解,也就是函数 的图像与 轴的交点的横坐标.所以: 方程 有实数解函数 有零点函数 的图像与 轴有交点 函数的零点与方程的解【零点的定义给出了求解函数零点的基本方法】(1)代数法:若方程 可解,其实数根就是函数 的零点.(2)几何法:若方程 难以直接求解,将其改为 ,进一步改为 ,在同一坐标系中分别画出两个函数 和 的图像,两图像交点的横坐标就是函数 的零点. . 零点存在定理【实例分析】以二次函数 为例,我们知道求函数 的零点,其实就是求方程 的实数解. 可以发现,在零点附近,函数的图像是连续不断的,并且穿过 轴.函数在端点 和 时的取值异号,即 ,于是函数在区间(2,4)内有零点;同样的, ,函数在区间(-2,0)内有零点. 一般地,如果函数 在区间 上的图像是一条连续不断的曲线,且有 ,那么函数在区间 内至少有一个零点.即存在 ,使得 ,这个t也就是方程 的解.这就是零点存在定理. 零点存在定理若 的图像在 上是不连续的,则 在 上没有零点. 那可不一定.下面这个函数在(-1,3)上照样有零点!函数 的图像在区间上是连续的,但 则 在 上没有零点. 这也不一定.下面这个函数 ,但函数在 上有零点! 零点存在定理【理解函数零点存在定理需要注意的问题】【1】① 函数 在区间 上的图像是一条连续不断的曲线.② ,这两个条件缺一不可,否则结论未必成立.【2】满足上述条件,则函数 的图像至少穿过 轴一次,即在区间 上函数 至少有一个零点,但是不确定到底有几个.【3】该定理是一个充分不必要条件.反过来,若函数 在区间 上有零点,则不一定有 成立. 零点存在定理【常见函数的零点】一个零点无零点 两个零点一个零点无零点无零点一个零点1 一个零点0无零点利用二分法求方程的近似解【二分法的概念】 假设我们知道函数 在区间(2,3)内存在一个零点,那么我们怎么求出这个零点呢? 一个直观的想法是:如果能将零点所在的范围尽量的缩小,那么在一定精确度的要求下,就可以得到符合要求的零点的近似值.为了方便,可以通过取中点的方法,逐步缩小零点的范围. 实际上大多数方程都不能像一元二次方程这样可以直接用公式求出精确解.在实际问题中,往往只需求出满足一定精确度的近似解. 我们知道求解二次函数 零点的方法,当 时,利用求根公式 就可以求出方程的解,也就是函数的零点. 利用二分法求方程的近似解【二分法的概念】 通过上述步骤,我们把零点的范围从(2,3)缩小到了(2.5,2.75),那么重复这个步骤,我们就可以把零点所在的范围缩小到满足一定精确度的区间,区间的任意一点都可以作为函输零点的近似值.为了方便,我们把区间的一个端点作为零点的近似值. 像这样,把在区间 上连续且 的函数 ,不断把零点区间一分为二逐步逼近零点,从而得到零点近似值的方法,叫做二分法. 一般地,称 为区间 的中点. 函数 在区间(2,3)上有零点,并且 ,取(2,3)的中点2.5,利用计算器求出 .因为 ,所以零点在区间(2.5,3)之间;再取区间(2.5,3)的中点2.75,算出 ,则零点在区间(2.5,2.75)之间… 利用二分法求方程的近似解【问题】二分法的理论依据是什么?【答】①二分法的理论依据是零点存在定理, 仅适用于函数的变号零点(函数图 像通过零点时函数值的符号改变)②二分法采用逐步逼近的思想,使函数零点所在的范围逐步缩小,也就是 逐步逼近函数的零点.要根据函数的性质尽可能的找到含有零点的更小 的区间,当区间的长度小到一定程度时,就可以取得可以解决实际问题 近似值.【步骤口诀】定区间,找中点,中间计算两边看;同号去,异号算,零点落在异号间;周而复始怎么办?精确度上来判断!利用二分法求方程的近似解【用二分法求函数零点近似值的步骤】【1】确定零点 的初始区间 ,验证 .【2】求区间 的中点c,计算 ,进一步确定零点所在区间:①如果 ,即c就是函数的零点; ②如果 ,则令 ; ③如果 ,则令 ; 【3】判断是否达到精确度 :若 ,则得到零点的近似值 , 否则重复步骤【2】 当 时,区间 任意一个值都可以作为零点近似值. 求函数零点个数的四种方法【方程法】求方程 的实数根.【图像法】对于不能用公式法求根的方程或者不易求出实数根的方程,可以将它与 对应的函数图像联系起来,并利用函数的性质找出零点,对于不易画出 图像的函数,可以转化为 ,分别画出 和 的图像,看两图像有几个交点.【奇偶性】结合函数的奇偶性,因为奇函数和偶函数的图像都有对称性,存在奇偶 性的函数的零点是成对出现的(0除外).【存在定理】若 ,函数 的图像在 上是一条连续不断的曲线 且单调,则函数在 内只有一个零点;如果函数连续不断但不单调, 那么在 内至少有一个零点. 对于 三个函数,定义域都是R,且在定义域内为单调增函数,所以都可以用二分法求零点近似值.【1】下列函数都可以用二分法求零点近似值吗,为什么?【解】 对于(2),作出图像如图:易知函数只有一个不变号零点,故无法用二分法求零点近似值. 即时巩固随堂小测1.函数y=ln x的零点是A.(0,0) B.x=0 C.x=1 D.不存在√2.下列各图象表示的函数中没有零点的是√3.若函数f(x)的图象在R上连续不断,且满足f(0)<0,f(1)>0,f(2)>0,则下列说法正确的是A.f(x)在区间(0,1)上一定有零点,在区间(1,2)上一定没有零点B.f(x)在区间(0,1)上一定没有零点,在区间(1,2)上一定有零点C.f(x)在区间(0,1)上一定有零点,在区间(1,2)上可能有零点D.f(x)在区间(0,1)上可能有零点,在区间(1,2)上一定有零点√15.若函数y=2-|x|-k有零点,则实数k的取值范围是_____.解析 y=2-|x|-k有零点,即k∈y=2-|x|的值域.而-|x|≤0,0<2-|x|≤20=1,∴y=2-|x|的值域为(0,1].(0,1]课堂小结1.方程f(x)=g(x)的根是函数f(x)与g(x)的图象交点的横坐标,也是函数y=f(x)-g(x)的图象与x轴交点的横坐标.2.在函数零点存在性定理中,要注意三点:(1)函数是连续的;(2)定理不可逆;(3)至少存在一个零点.3.解决函数的零点存在性问题常用的办法有三种:(1)用定理;(2)解方程;(3)用图象.4.函数与方程有着密切的联系,有些方程问题可以转化为函数问题求解,同样,函数问题有时可以转化为方程问题,这正是函数与方程思想的基础.谢 谢!
4.5函数的应用(二)第四章4.5.1 函数的零点与方程的解4.5.2用二分法求方程的近似解学习目标1.了解函数零点的定义.2.了解函数的零点与函数对应方程的根的关系.3.能够根据函数零点的判定方法判断函数零点所在的区间.4.了解二分法求方程近似解的原理,能借助计算器用二分法求函数零点的近似值.5.根据具体函数的图象,能够用二分法求相应方程的近似值.核心素养:数学抽象、逻辑推理、数学运算新知学习函数的零点与方程的解【导学】如何求二次方程 的实数根? 【答】由根的判别式 得: 对于一个一般的函数,也可以这么算吗?它们有什么异同点?函数的零点与方程的解【函数零点的定义】与二次函数的零点一样,对于一般函数 ,我们把使得 的实数 叫做函数 的零点. 这样,函数 的零点就是方程 的实数解,也就是函数 的图像与 轴的交点的横坐标.所以: 方程 有实数解函数 有零点函数 的图像与 轴有交点 函数的零点与方程的解【零点的定义给出了求解函数零点的基本方法】(1)代数法:若方程 可解,其实数根就是函数 的零点.(2)几何法:若方程 难以直接求解,将其改为 ,进一步改为 ,在同一坐标系中分别画出两个函数 和 的图像,两图像交点的横坐标就是函数 的零点. . 零点存在定理【实例分析】以二次函数 为例,我们知道求函数 的零点,其实就是求方程 的实数解. 可以发现,在零点附近,函数的图像是连续不断的,并且穿过 轴.函数在端点 和 时的取值异号,即 ,于是函数在区间(2,4)内有零点;同样的, ,函数在区间(-2,0)内有零点. 一般地,如果函数 在区间 上的图像是一条连续不断的曲线,且有 ,那么函数在区间 内至少有一个零点.即存在 ,使得 ,这个t也就是方程 的解.这就是零点存在定理. 零点存在定理若 的图像在 上是不连续的,则 在 上没有零点. 那可不一定.下面这个函数在(-1,3)上照样有零点!函数 的图像在区间上是连续的,但 则 在 上没有零点. 这也不一定.下面这个函数 ,但函数在 上有零点! 零点存在定理【理解函数零点存在定理需要注意的问题】【1】① 函数 在区间 上的图像是一条连续不断的曲线.② ,这两个条件缺一不可,否则结论未必成立.【2】满足上述条件,则函数 的图像至少穿过 轴一次,即在区间 上函数 至少有一个零点,但是不确定到底有几个.【3】该定理是一个充分不必要条件.反过来,若函数 在区间 上有零点,则不一定有 成立. 零点存在定理【常见函数的零点】一个零点无零点 两个零点一个零点无零点无零点一个零点1 一个零点0无零点利用二分法求方程的近似解【二分法的概念】 假设我们知道函数 在区间(2,3)内存在一个零点,那么我们怎么求出这个零点呢? 一个直观的想法是:如果能将零点所在的范围尽量的缩小,那么在一定精确度的要求下,就可以得到符合要求的零点的近似值.为了方便,可以通过取中点的方法,逐步缩小零点的范围. 实际上大多数方程都不能像一元二次方程这样可以直接用公式求出精确解.在实际问题中,往往只需求出满足一定精确度的近似解. 我们知道求解二次函数 零点的方法,当 时,利用求根公式 就可以求出方程的解,也就是函数的零点. 利用二分法求方程的近似解【二分法的概念】 通过上述步骤,我们把零点的范围从(2,3)缩小到了(2.5,2.75),那么重复这个步骤,我们就可以把零点所在的范围缩小到满足一定精确度的区间,区间的任意一点都可以作为函输零点的近似值.为了方便,我们把区间的一个端点作为零点的近似值. 像这样,把在区间 上连续且 的函数 ,不断把零点区间一分为二逐步逼近零点,从而得到零点近似值的方法,叫做二分法. 一般地,称 为区间 的中点. 函数 在区间(2,3)上有零点,并且 ,取(2,3)的中点2.5,利用计算器求出 .因为 ,所以零点在区间(2.5,3)之间;再取区间(2.5,3)的中点2.75,算出 ,则零点在区间(2.5,2.75)之间… 利用二分法求方程的近似解【问题】二分法的理论依据是什么?【答】①二分法的理论依据是零点存在定理, 仅适用于函数的变号零点(函数图 像通过零点时函数值的符号改变)②二分法采用逐步逼近的思想,使函数零点所在的范围逐步缩小,也就是 逐步逼近函数的零点.要根据函数的性质尽可能的找到含有零点的更小 的区间,当区间的长度小到一定程度时,就可以取得可以解决实际问题 近似值.【步骤口诀】定区间,找中点,中间计算两边看;同号去,异号算,零点落在异号间;周而复始怎么办?精确度上来判断!利用二分法求方程的近似解【用二分法求函数零点近似值的步骤】【1】确定零点 的初始区间 ,验证 .【2】求区间 的中点c,计算 ,进一步确定零点所在区间:①如果 ,即c就是函数的零点; ②如果 ,则令 ; ③如果 ,则令 ; 【3】判断是否达到精确度 :若 ,则得到零点的近似值 , 否则重复步骤【2】 当 时,区间 任意一个值都可以作为零点近似值. 求函数零点个数的四种方法【方程法】求方程 的实数根.【图像法】对于不能用公式法求根的方程或者不易求出实数根的方程,可以将它与 对应的函数图像联系起来,并利用函数的性质找出零点,对于不易画出 图像的函数,可以转化为 ,分别画出 和 的图像,看两图像有几个交点.【奇偶性】结合函数的奇偶性,因为奇函数和偶函数的图像都有对称性,存在奇偶 性的函数的零点是成对出现的(0除外).【存在定理】若 ,函数 的图像在 上是一条连续不断的曲线 且单调,则函数在 内只有一个零点;如果函数连续不断但不单调, 那么在 内至少有一个零点. 对于 三个函数,定义域都是R,且在定义域内为单调增函数,所以都可以用二分法求零点近似值.【1】下列函数都可以用二分法求零点近似值吗,为什么?【解】 对于(2),作出图像如图:易知函数只有一个不变号零点,故无法用二分法求零点近似值. 即时巩固随堂小测1.函数y=ln x的零点是A.(0,0) B.x=0 C.x=1 D.不存在√2.下列各图象表示的函数中没有零点的是√3.若函数f(x)的图象在R上连续不断,且满足f(0)<0,f(1)>0,f(2)>0,则下列说法正确的是A.f(x)在区间(0,1)上一定有零点,在区间(1,2)上一定没有零点B.f(x)在区间(0,1)上一定没有零点,在区间(1,2)上一定有零点C.f(x)在区间(0,1)上一定有零点,在区间(1,2)上可能有零点D.f(x)在区间(0,1)上可能有零点,在区间(1,2)上一定有零点√15.若函数y=2-|x|-k有零点,则实数k的取值范围是_____.解析 y=2-|x|-k有零点,即k∈y=2-|x|的值域.而-|x|≤0,0<2-|x|≤20=1,∴y=2-|x|的值域为(0,1].(0,1]课堂小结1.方程f(x)=g(x)的根是函数f(x)与g(x)的图象交点的横坐标,也是函数y=f(x)-g(x)的图象与x轴交点的横坐标.2.在函数零点存在性定理中,要注意三点:(1)函数是连续的;(2)定理不可逆;(3)至少存在一个零点.3.解决函数的零点存在性问题常用的办法有三种:(1)用定理;(2)解方程;(3)用图象.4.函数与方程有着密切的联系,有些方程问题可以转化为函数问题求解,同样,函数问题有时可以转化为方程问题,这正是函数与方程思想的基础.谢 谢!
相关资料
更多









