北师大版九年级下册5 二次函数与一元二次方程多媒体教学ppt课件

这是一份北师大版九年级下册5 二次函数与一元二次方程多媒体教学ppt课件，共28页。PPT课件主要包含了b2－4ac，复习回顾，自主学习，合作探究，归纳总结，学以致用，知识升华，当堂检测，课堂小结，课外作业等内容，欢迎下载使用。
1．通过探索，使学生理解二次函数与一元二次方程之间的联系。2．使学生能够运用二次函数及其图象、性质解决实际问题，提高学生用数学的意识。3．进一步培养学生综合解题能力，渗透数形结合思想。
用函数图象法求方程的解以及提高学生综合解题能力是教学的重点。
提高学生综合解题能力，渗透数形结合的思想是教学的难点
1.一元二次方程ax2+bx+c=0 根的判别式是什么？ 它的根有哪些情况？
2.解下列一元二次方程：（1）x2+3x=0 （2）x2－4x+4=0 （3）x2-2x+3=0.
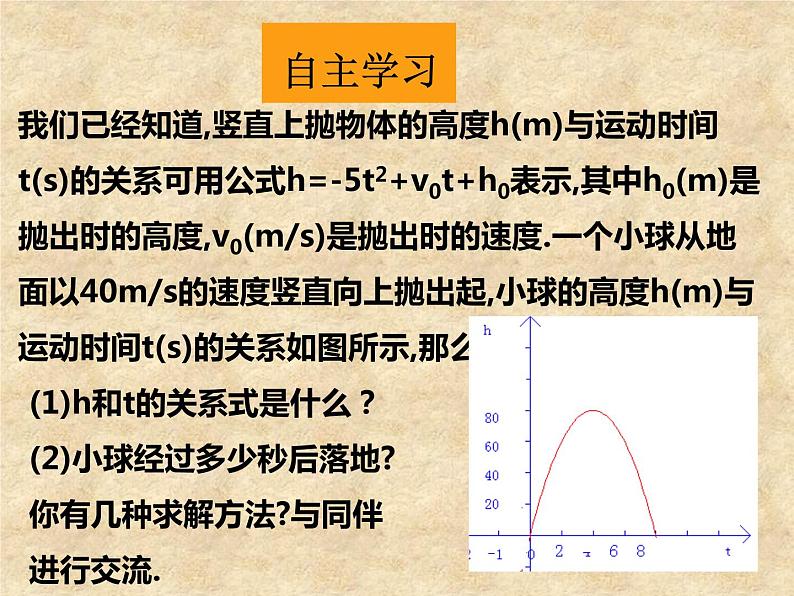
我们已经知道,竖直上抛物体的高度h(m)与运动时间t(s)的关系可用公式h=-5t2+v0t+h0表示,其中h0(m)是抛出时的高度,v0(m/s)是抛出时的速度.一个小球从地面以40m/s的速度竖直向上抛出起,小球的高度h(m)与运动时间t(s)的关系如图所示,那么：
(1)h和t的关系式是什么？(2)小球经过多少秒后落地?你有几种求解方法?与同伴进行交流.
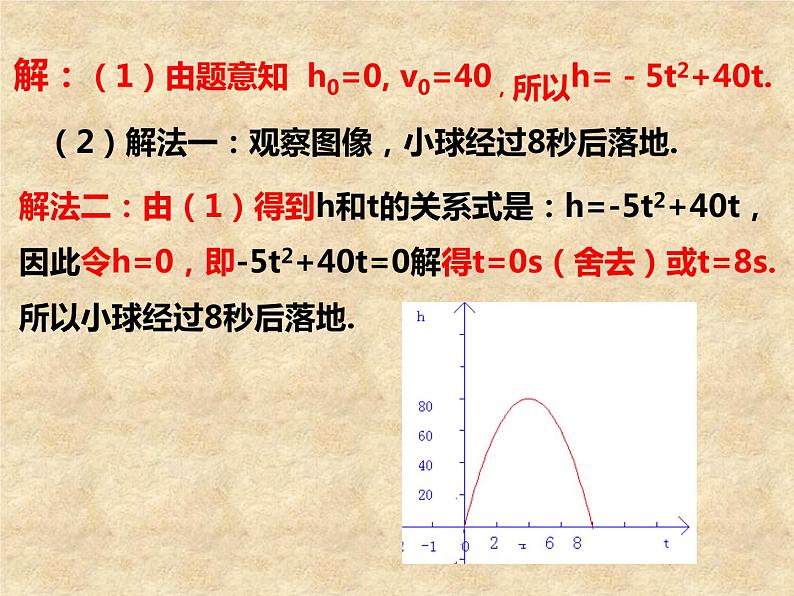
解：（1）由题意知 h0=0, v0=40，所以h=－5t2+40t.
（2）解法一：观察图像，小球经过8秒后落地.
解法二：由（1）得到h和t的关系式是：h=-5t2+40t，因此令h=0，即-5t2+40t=0解得t=0s（舍去）或t=8s.所以小球经过8秒后落地.
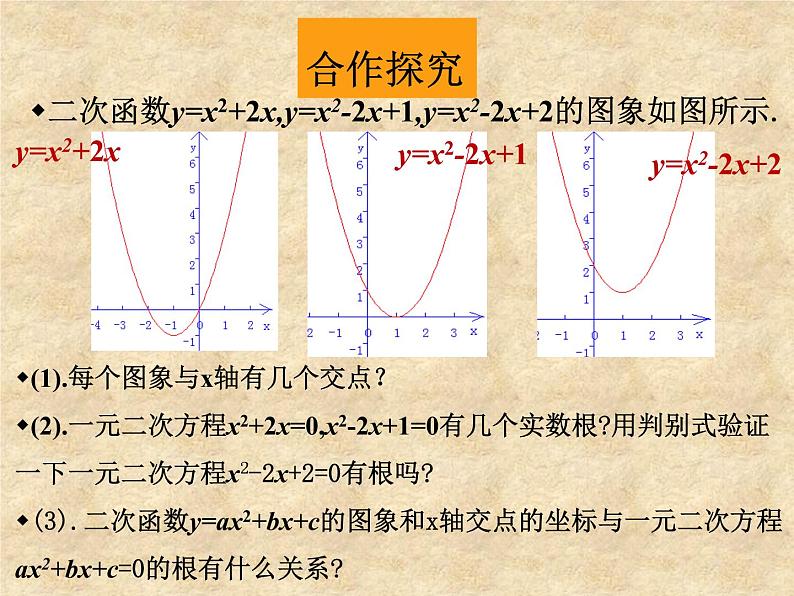
(1).每个图象与x轴有几个交点？(2).一元二次方程x2+2x=0,x2-2x+1=0有几个实数根?用判别式验证一下一元二次方程x2-2x+2=0有根吗?(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?
二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示.
二次函数y=x2+2x的图象与x轴有几个交点？
与x轴有2个交点：（-2，0）和（0，0）
一元二次方程x2+2x=0有几个根？
解：x(x+2)=0 x=0或x+2=0 ∴ x1=-2，x2=0
二次函数y=x2-2x+1的图象与x轴有几个交点？
与x轴有1个交点：（1，0）
一元二次方程x2-2x+1=0有几个根？
解： (x-1)2=0 ∴ x1=x2=1
二次函数y=x2-2x+2的图象与x轴有几个交点？
一元二次方程x2-2x+2=0有几个根？
解：∵△=(-2)2-4×1×2 =-4﹤0 ∴ 原方程无实根
二次函数y=ax2+bx+c的图象和x轴交点的横坐标就是一元二次方程ax2+bx+c=0的根.
3 抛物线y=x2-4x+4与轴有___个交点，坐标是________ 。
1 若方程ax2+bx+c=0的根为x1=-2和x2=3，则二次函数 y=ax2+bx+c的图象与x轴交点坐标是______________ 。
2 抛物线y=0.5x2-x+3与x轴的交点情况是（ ） A 两个交点 B 一个交点 C 没有交点 D 画出图象后才能说明
（-2，0）和（3，0）
在本节一开始的小球上抛问题中,何时小球离地面的高度是60m?你是如何知道的?
∴抛出去后第2秒和第6秒时，离地面60米
解得：t1=2 t2=6
h=－5t2+40t.
2.若抛物线y=ax2+bx+c,当 a>0,c