人教A版 (2019)选择性必修 第一册1.1 空间向量及其运算当堂检测题

这是一份人教A版 (2019)选择性必修 第一册1.1 空间向量及其运算当堂检测题，文件包含专题11利用空间向量法求空间中的距离特色专题卷人教A版选择性必修第一册解析版docx、专题11利用空间向量法求空间中的距离特色专题卷人教A版选择性必修第一册原卷版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
专题1.1 利用空间向量法求空间中的距离（特色专题卷）
考试时间：120分钟；满分：150分
姓名：___________班级：___________考号：___________
考卷信息：
本卷试题共22题，单选8题，多选4题，填空4题，解答6题，满分150分，限时150分钟，试卷紧扣教材，细分题组，精选一年好题，两年真题，练基础，提能力！
一． 选择题（共8小题，满分40分，每小题5分）
1.（2020秋•临渭区期末）在空间直角坐标系中，点M的坐标为（﹣1，0，2），则点M到原点O的距离为（　　）
A．1 B．2 C．3 D．5
【分析】利用空间中两点间距离公式直接求解．
【解答】解：在空间直角坐标系中，点M的坐标为（﹣1，0，2），
则点M到原点O的距离为：
|MO|=(-1)2+02+22=5．
故选：D．
2.（2021春•瑶海区月考）已知空间直角坐标系O﹣xyz中的点A（2，﹣1，﹣3）关于xOy平面的对称点为B，则|AB|的值为（　　）
A．14 B．4 C．6 D．210
【分析】利用点关于面的对称点的特点求出点B，然后由空间两点间距离公式求解即可．
【解答】解：A（2，﹣1，﹣3）关于xOy平面的对称点为B（2，﹣1，3），
所以|AB|=(2-2)2+(-1+1)2+(-3-3)2=6．
故选：C．
3．（2019•西湖区校级模拟）空间直角坐标系中，点A（1，2，3）关于xOy平面的对称点为点B，关于原点的对称点为点C，则B，C间的距离为（　　）
A．5 B．14 C．25 D．214
【分析】推导出B（1，2，﹣3），C（﹣1，﹣2，﹣3），由此能求出B，C间的距离．
【解答】解：空间直角坐标系中，点A（1，2，3）关于xOy平面的对称点为点B，
关于原点的对称点为点C，
∴B（1，2，﹣3），C（﹣1，﹣2，﹣3），
则B，C间的距离为|BC|=(1+1)2+(2+2)2+(-3+3)2=25．
故选：C．
4．已知M（4，3，﹣1），记M到x轴的距离为a，M到y轴的距离为b，M到z轴的距离为c，则（　　）
A．a＞b＞c B．c＞b＞a C．c＞a＞b D．b＞c＞a
【分析】根据空间点（x，y，x）到x轴的距离等于y2+z2，到y轴的距离等于x2+z2，到z轴的距离等于x2+y2，代入数据即可求出所求．
【解答】解：∵M（4，3，﹣1）
∴M到x轴的距离a=32+(-1)2=9+1=10，
M到y轴的距离b=42+(-1)2=17，
M到z轴的距离c=42+32=5
∵5＞17＞10
∴c＞b＞a
故选：B．
5．（2020秋•太原期末）已知a→=（1﹣t，1，0），b→=（2，t，t），则|b→-a→|的最小值是（　　）
A．1 B．2 C．3 D．5
【分析】利用向量的坐标运算法则得到b→-a→=（1+t，t﹣1，t），从而|b→-a→|=(1+t)2+(t-1)2+t2=3t2+2，由此能求出当t＝0时，|b→-a→|取最小值2．
【解答】解：∵a→=（1﹣t，1，0），b→=（2，t，t），
∴b→-a→=（1+t，t﹣1，t），
∴|b→-a→|=(1+t)2+(t-1)2+t2
=3t2+2，
∴当t＝0时，|b→-a→|取最小值2．
故选：B．
6.（2015春•广安校级月考）已知直线l的方向向量为a→=（﹣1，0，1），点A（1，2，﹣1）在l上，则点P（2，﹣1，2）到l的距离为（　　）
A．15 B．4 C．17 D．32
【分析】根据点P到直线l的距离为|PA→|•sin＜a→，PA→＞，分别计算向量的模长与夹角的正弦值即可．
【解答】解：根据题意，得；
PA→=（﹣1，3，﹣3），
a→=（﹣1，0，1），
∴cos＜a→，PA→＞=1+0-32×19=-219，
∴sin＜a→，PA→＞=1719；
又∵|PA→|=19，
∴点P（2，﹣1，2）到直线l的距离为
|PA→|sin＜a→，PA→＞=19×1719=17．
故选：C．
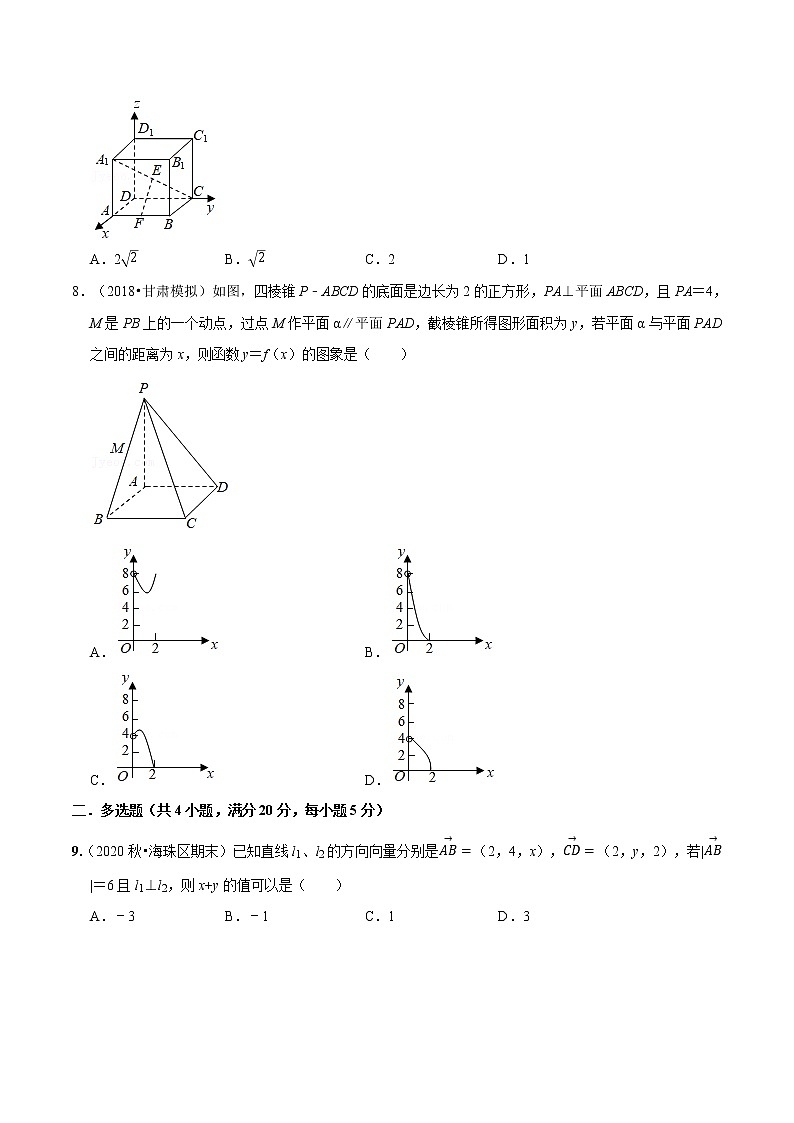
7．（2020秋•仁寿县校级期中）如图，在空间直角坐标系中，有一棱长为2的正方体ABCD﹣A1B1C1D1，A1C的中点E到AB的中点F的距离为（　　）

A．22 B．2 C．2 D．1
【分析】利用正方体的结构特征，先分别求出E和F的坐标，再用两点间距离公式求解．
【解答】解：在空间直角坐标系中，有一棱长为2的正方体ABCD﹣A1B1C1D1
∴A1（2，0，2），C（0，2，0），A1C的中点E（1，1，1），
A（2，0，0），B（2，2，0），AB的中点F（2，1，0），
∴A1C的中点E到AB的中点F的距离为：
|EF|=(2-1)2+(1-1)2+(0-1)2=2．
故选：B．

8．（2018•甘肃模拟）如图，四棱锥P﹣ABCD的底面是边长为2的正方形，PA⊥平面ABCD，且PA＝4，M是PB上的一个动点，过点M作平面α∥平面PAD，截棱锥所得图形面积为y，若平面α与平面PAD之间的距离为x，则函数y＝f（x）的图象是（　　）

A． B．
C． D．
【分析】过M作MN⊥平面ABCD，交AB于N，过N作NQ∥AD，交CD于Q，过Q作QH∥PD，交PC于H，连结MH，则平面MNQH是所求的平面α，由此能求出结果．
【解答】解：过M作MN⊥平面ABCD，交AB于N，过N作NQ∥AD，交CD于Q，
过Q作QH∥PD，交PC于H，连结MH，
则平面MNQH是所求的平面α，
∵过点M作平面α∥平面PAD，
截棱锥所得图形面积为y，平面α与平面PAD之间的距离为x，
∴2-x2=MN4，解得MN＝4﹣2x，
ANAB=PMPB=MHBC，即x2=MH2，∴MH＝x，NQ＝2，
∴函数y＝f（x）=x+22⋅(4-2x)=-x2+4，（0＜x＜2）．
∴函数y＝f（x）的图象如下图．

故选：D．
二． 多选题（共4小题，满分20分，每小题5分）
9.（2020秋•海珠区期末）已知直线l1、l2的方向向量分别是AB→=（2，4，x），CD→=（2，y，2），若|AB→|＝6且l1⊥l2，则x+y的值可以是（　　）
A．﹣3 B．﹣1 C．1 D．3
【分析】由|AB→|＝6且l1⊥l2，列出方程组，求出x，y的值，由此能求出x+y的值．
【解答】解：∵直线l1、l2的方向向量分别是AB→=（2，4，x），CD→=（2，y，2），|AB→|＝6且l1⊥l2，
∴4+16+x2=64+4y+2x=0，解得x2=16x+2y+2=0，
∴x=4y=-3或x=-4y=1，
∴x+y＝1或x+y＝﹣3．
故选：AC．
10.如图，已知E是棱长为2的正方体的棱BC的中点，F是棱的中点，设点D到面的距离为d，直线DE与面所成的角为，面与面AED的夹角为，则   
A. 面  B.
C.       D.
【分析】
本题考查了利用空间向量求线面和面面的夹角、考查了利用空间向量判定线面的垂直关系，考查了利用空间向量求点到面的距离，以A为坐标原点，，，的方向为x，y，z轴的正方向，建立空间直角坐标系，利用空间向量法可分析判断各选项是否正确.
【解答】
解：以A为坐标原点，，，的方向为x，y，z轴的正方向，建立空间直角坐标系，
则，，，，，，
所以，，，
设平面的法向量为，则由，得
令，则，，故
，不存在使，即与不共线，与面不垂直，
故A不正确；
又，，故B正确；
又〈，〉正确；
又为平面AED的一个法向量，
，故D正确.
故选
11.如图，在直三棱柱中，，，D，E，F分别为AC，，AB的中点．则下列结论正确的是


A. 与EF相交 B. 平面DEF
C. EF与所成的角为 D. 点到平面DEF的距离为
【分析】
本题主要考查异面直线的位置关系，线面平行的判定，异面直线所成角以及点到面的距离，利用空间直角坐标系是解题的关键，考查学生的思维能力及综合分析能力，属较难题.
利用异面直线的位置关系，线面平行的判定方法，利用空间直角坐标系异面直线所成角和点到面的距离，对各个选项逐一判断.
【解答】
解：对选项A，由图知平面，平面，且
由异面直线的定义可知与EF异面，故A错误；
对于选项B，在直三棱柱中， 
，F分别是AC，AB的中点，
，
 
又平面DEF，平面DEF，
 平面DEF，故B正确；
对于选项C，由题意，建立如图所示的空间直角坐标系，

则，，，，，
，，，
，
，
，
与所成的角为故C正确；
对于选项D，设向量是平面DEF的一个法向量．
，，
由即得
取，则，，
设点到平面DEF的距离为
又，
，
点到平面DEF的距离为，故D正确．
故选
12.（2020秋•沧州期中）在三棱锥P﹣ABC中，PA＝PB＝PC＝6，AB＝BC＝AC＝62，E为PA的中点，D，F分别在AC，PB上，且AD：CD＝PF：BF＝2：1，则（　　）
A．PA⊥BC
B．AB∥平面DEF
C．点C到平面DEF的距离是32613
D．平面DEF与平面ABC所成的锐二面角的余弦值为47839
【分析】推出PA⊥PB，PA⊥PC，PB⊥PC，以P为原点，以PB，PC，PA的方向分别为x，y，z轴的正方向，建立如图所示的空间直角坐标系P﹣xyz，推出PA→•BC→=0，判断A；求出平面DEF的法向量，通过AB→•m→≠0，判断B；利用空间距离公式求解判断C；求出二面角的余弦函数值判断D．
【解答】解：因为PA=PB=PC=6，AB=BC=AC=62，
所以PA2+PB2＝AB2，PA2+PC2＝AC2，PB2+PC2＝BC2，
所以PA⊥PB，PA⊥PC，PB⊥PC，
故以P为原点，以PB，PC，PA的方向分别为x，y，z轴的正方向，建立如图所示的空间直角坐标系P﹣xyz，
则P（0，0，0），A（0，0，6），B（6，0，0），C（0，6，0），
D（0，4，2），E（0，0，3），F（4，0，0），
从而PA→=（0，0，6），BC→=（﹣6，6，0），AB→=（6，0，﹣6），DF→=（4，﹣4，﹣2），EF→=（4，0，﹣3），
因为PA→•BC→=0，所以PA→⊥BC→，则A正确；
设平面DEF的法向量为m→=（x，y，z），
m→⋅EF→=0m→⋅DF→=0，即4x-3z=04x-4y-2z=0，令x＝3，得m→=（3，1，4），
因为AB→•m→=6×3+0﹣6×4＝﹣6≠0，所以AB与平面DEF不平行，则B错误；
因为CE→=（0，﹣6，3），所以点C到平面DEF的距离是||CE→|cos〈CE→，m→〉|=CE→⋅m→|m→|=0-6×1+3×49+1+16=32613，则C正确；
设平面ABC的法向量为n→=（x1y1，z1），令x1＝1，得n→=（1，1，1），
所以cos〈m→，n→〉=m→⋅n→|m→||n→|=3+1+426×3=47839，则D正确

故选：ACD．
三． 填空题（共4小题，满分20分，每小题5分
13.（2020秋•驻马店期末）已知空间直角坐标系中的点M，N的坐标分别为（5，5，8），（﹣1，1，4）．则线段MN的中点到坐标原点的距离为　7　．
【分析】线段MN的中点坐标为：（2，3，6），由此能求出线段MN的中点到坐标原点的距离．
【解答】解：空间直角坐标系中的点M，N的坐标分别为（5，5，8），（﹣1，1，4）．
线段MN的中点坐标为：（2，3，6），
则线段MN的中点到坐标原点的距离为：22+32+62=7．
故答案为：7．
14．（2020•南昌期中）两平行平面α，β分别经过坐标原点O和点A（2，1，1），且两平面的一个法向量n→=（﹣1，0，1），则两平面间的距离是　22　．
【分析】利用两个平面的距离公式：d=|n→⋅OA→||n→|即可得出．
【解答】解：∵两平行平面α，β分别经过坐标原点O和点A（2，1，1），OA→=(2，1，1)，
且两平面的一个法向量n→=（﹣1，0，1），
∴两平面间的距离=|n→⋅OA→||n→|=|-2+0+1|2=22．
故答案为：22．
15．（2020秋•路南区校级期中）已知点A（﹣1，﹣2，1），B（2，2，2），点P在Z轴上，且点P到A，B的距离相等，则点P的坐标为　（0，0，3）　．
【分析】设P（0，0，z）．由于点P到A，B的距离相等，可得12+22+(z-1)2=22+22+(2-z)2，解出即可．
【解答】解：设P（0，0，z）．
∵点P到A，B的距离相等，
∴12+22+(z-1)2=22+22+(2-z)2，
化为2z＝6，解得z＝3．
∴点P的坐标（0，0，3）．
故答案为：（0，0，3）．
16．（2020秋•柳南区校级月考）在三棱锥P﹣ABC中，PA，PB，PC两两垂直，且PA＝1，PB＝2，PC＝3，则点P到△ABC的重心G的距离为　143　．
【分析】由题意画出图形，建立空间直角坐标系，确定G的坐标，利用空间两点间的距离公式求出PG即可．
【解答】解：PA，PB，PC两两垂直，以P为坐标原点，PA、PB、PC所在直线分别为x，y，z轴，建立空间直角坐标系，且PA＝1，PB＝2，PC＝3，
所以P（0，0，0），A（1，0，0），B（0，2，0），C（0，0，3），
△ABC的重心G的坐标为（13，23，1），
PG=(13-0)2+(23-0)2+(1-0)2=143．
∴点P到△ABC的重心G的距离是143．
故答案为：143．

四． 解答题（共6小题，满分70分）
17.在坐标面yOz内，求与三个已知点A（3，1，2），B（4，﹣2，﹣2），C（0，5，1）等距离的点D的坐标．
【分析】根据点在坐标面yOz内，设出点的坐标（0，y，z），根据点到A、B、C的距离相等，写出关于y、z的方程，解方程即可得到点的坐标．
【解答】解：设yOz平面内一点D（0，y，z）与A，B，C三点距离相等，
则有|AD|2＝9+（1﹣y）2+（2﹣z）2，
|BD|2＝16+（2+y）2+（2+z）2，
|CD|2＝（5﹣y）2+（1﹣z）2，
由|AD|＝|BD|，及|AD|＝|CD|，
得9+(1-y)2+(2-z)2=16+(2+y)2+(2+z)29+(1-y)2+(2-z)2=(5-y)2+(1-z)2
化简可得3y+4z+5=04y-z-6=0
解得y=1z=-2
∴点D（0，1，﹣2）为yOz平面内到A，B，C三点等距离的点．
18.（2020秋•启东市校级期中）已知A（3，1，3），B（1，5，0），求：
（1）线段AB的中点坐标和长度；
（2）到A，B两点距离相等的点P（x，y，z）的坐标x，y，z满足的条件．
【分析】（1）利用中点坐标公式和两点间距离公式能出AB中点坐标和线段长．
（2）由PA＝PB，利用两点间距离公式能求出点P（x，y，z）的坐标x，y，z满足的条件．
【解答】解：（1）∵A（3，1，3），B（1，5，0），
∴AB中点坐标（2，3，32）．AB→=（﹣2，4，﹣3），
∴|AB→|=29．
（2）A（3，1，3），B（1，5，0），P（x，y，z），
由PA＝PB得：
(x-3)2+(y-1)2+(z-3)2=(x-1)2+(y-5)2+z2，
整理得：4x﹣8y+6z+7＝0．
19.如图所示，平面α⊥平面β，AD⊥AC，BC⊥AC，AD＝3，BC＝8．AC＝5．
（1）AD⊥α成立吗？
（2）求BD的长度．

【分析】（1）由面面垂直的性质即可证明AD⊥α；
（2）由BD→=BC→+CA→+AD→，能求出BD的长度
【解答】解：（1）AD⊥α．证明如下：
∵平面α⊥平面β，平面α∩平面β＝AC，
AD⊥AC，AD⊂平面β，
∴AD⊥α．
（2）∵BD→=BC→+CA→+AD→，
∴BD→2=（BC→+CA→+AD→）2=BC→2+CA→2+AD→2=64+25+9＝98，
∴BD的长度|BD→|=98=72．

20.（2020•闵行区校级期末）已知平行六面体ABCD﹣A1B1C1D1，AD＝AA1＝AB＝1，∠A1AB＝∠DAB＝∠DAA1＝60°，A1C1→=3NC1→，D1B→=4MB→，设AB→=a→，AD→=b→，AA1→=c→；
（1）试用a→、b→、c→表示MN→；
（2）求MN的长度；

【分析】（1）MN→=MD1→+D1A1→+A1N→=-34D1B→-AD→+23A1C1→=-34（D1D→+DB→）-AD→+23（AB→+AD→），由此能求出结果．
（2）由MN→=-112a→+512b→+34c→．AD＝AA1＝AB＝1，∠A1AB＝∠DAB＝∠DAA1＝60°，由此能求出MN的长度．
【解答】解：（1）MN→=MD1→+D1A1→+A1N→
=-34D1B→-AD→+23A1C1→
=-34（D1D→+DB→）-AD→+23（AB→+AD→）
=34c→-34（a→-b→）-b→+23（a→+b→）
=-112a→+512b→+34c→．
（2）∵MN→=-112a→+512b→+34c→，
∴MN→2=（-112a→+512b→+34c→）2
=1144+25144+916-5144-348+1548=138144=2324．
∴MN的长度为|MN→|=13812．
21.如图在四棱锥中，底面ABCD为矩形，底面ABCD，E是AB上一点，，，，

求二面角的大小；
求点B到平面PEC的距离．
【答案】解：以D为原点，向量，，的方向分别为x，y，z轴的正方向建立空间直角坐标系，
，，，
，
设平面PEC的一个法向量为，
由，，
得，令，则
所以，
取平面PCD的一个法向量为，
设二面角的大小为，由图可知为锐角.
，，
即二面角的大小为
由知平面PEC的一个法向量为，
又，，
点B到平面PEC的距离

【解析】本题考查了利用空间向量求点面之间的距离，利用空间向量求面面的夹角.属于基础题.
以D为原点，向量，，的方向分别为x，y，z轴的正方向建立空间直角坐标系，分别求得平面PEC的一个法向量、平面PCD的一个法向量，故得二面角的大小；
由知平面PEC的一个法向量为，故得，故可由空间向量法求得点B到平面PEC的距离．
22.（2020秋•台江区校级期中）如图，在四棱锥P﹣ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB=3，BC＝1，PA＝2，E为PD的中点．
（1）求cos＜AC→，PB→＞的值；
（2）在侧面PAB内找一点N，使NE⊥平面PAC，并求出N到AB和AP的距离．

【分析】（1）以A为原点，AB为x轴，AD为y轴，AP为z轴，建立空间直角坐标系，利用向量法能求出cos〈AC→，PB→〉的值．
（2）设在侧面PAB内找一点N（a，0，c），使NE⊥平面PAC，利用向量法列方程组求出N（36，0，1），由此能求了N到AB和AP的距离．
【解答】解：（1）在四棱锥P﹣ABCD中，底面ABCD为矩形
侧棱PA⊥底面ABCD，AB=3，BC＝1，PA＝2，E为PD的中点．
以A为原点，AB为x轴，AD为y轴，AP为z轴，建立空间直角坐标系，
则A（0，0，0），C（3，1，0），P（0，0，2），B（3，0，0），
AC→=（3，1，0），PB→=（3，0，-2），
∴cos〈AC→，PB→〉=AC→⋅PB→|AC→|⋅|PB→|=34⋅7=3714．
（2）设在侧面PAB内找一点N（a，0，c），使NE⊥平面PAC，
D（0，1，0），E（0，12，1），NE→=（﹣a，12，1﹣c），
AP→=（0，0，2），AC→=（3，1，0），
∴NE→⋅AP→=2(1-c)=0NE→⋅AC→=-3a+12=0，解得a=36，c＝1，
∴N（36，0，1），
∴N到AB的距离为1，N 到AP的距离为36．