第八章 8.1.1 向量数量积的概念 8.1.2 向量数量积的运算律（课件PPT）

这是一份第八章 8.1.1 向量数量积的概念 8.1.2 向量数量积的运算律（课件PPT），共60页。

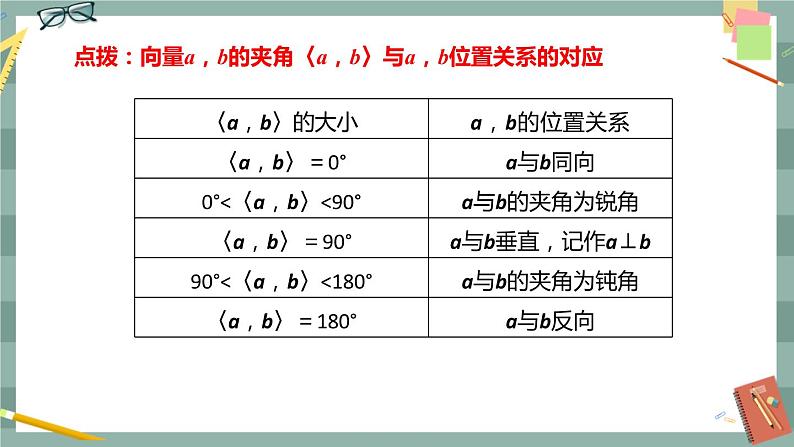
第八章　向量的数量积与三角恒等变换8.1.1 向量的数量积的概念8.1.2 向量的数量积的运算律1.掌握平面向量数量积的几何意义.2.掌握平面向量数量积的性质及运算律.重点：平面向量数量积的定义及应用.难点：平面向量数量积运算律的理解及应用.一、两个向量的夹角    π 点拨：向量a，b的夹角〈a，b〉与a，b位置关系的对应二、向量数量积的定义1.定义一般地，当a与b都是非零向量时，称|a||b|cos〈a，b〉为向量a与b的数量积（也称为内积），记作a·b，即a·b＝|a||b|cos〈a，b〉.由定义可知，两个非零向量a与b的数量积是一个实数，这与向量的加法、减法以及数乘向量的结果仍是一个向量不同. 观察两个非零向量a与b的数量积的定义可知，a·b的符号由cos〈a，b〉决定，从而也就是由〈a，b〉的大小决定.例如，右图中，a·b>0，a·c＝0，a·d<0.这就是说，两个非零向量的数量积既可以是正数，也可以是零，还可以是负数.     三、向量的投影与向量数量积的几何意义     图（1）  图（3）图（2）2.向量投影的数量一般地，如果a，b都是非零向量，则称|a|cos〈a，b〉为向量a在向量b上的投影的数量.投影的数量与投影的长度有关，但是投影的数量既可能是非负数，也可能是负数.|a|cos〈a，b〉的符号由cos〈a，b〉确定，取决于〈a，b〉的取值范围！3.向量数量积的几何意义因为a·b＝|a||b|cos〈a，b〉＝（|a|cos〈a，b〉）|b|，所以两个非零向量a，b的数量积a·b，等于a在向量b上的投影的数量与b的模的乘积.特别地，当e为单位向量时，因为|e|＝1，所以a·e＝|a|cos〈a，e〉，即任意向量与单位向量的数量积，等于这个向量在单位向量e上的投影的数量. 四、向量数量积的运算律 我们已经知道，很多运算都满足一定的运算律. 例如，向量的加法满足交换律，数乘向量对加法满足分配律，即对任意向量a，b以及实数λ，有a+b＝b+a，λ（a+b）＝λa+λb.根据向量数量积的定义，探讨向量数量积的运算满足哪些运算律，并说明理由. 证明：当a，b是两个非零向量时， 因为〈a，b〉＝〈b，a〉， 所以根据a·b＝|a||b|cos〈a，b〉， b·a＝|b||a|cos〈b，a〉 可知a·b＝b·a， 即向量的数量积满足交换律. 证明：当a，b都是非零向量且λ≠0时，（1）如果λ>0，则|λa|＝λ|a|，且λa的方向与a的方向相同，从而〈λa，b〉＝〈a，b〉， 因此（λa）·b＝|λa||b|cos〈λa，b〉 ＝λ|a||b|cos〈a，b〉 ＝λ（a·b）；（2）如果λ<0，则|λa|＝-λ|a|，且λa的方向与a的方向相反，从而〈λa，b〉＝π-〈a，b〉， 因此（λa）·b＝|λa||b|cos〈λa，b〉 ＝-λ|a||b|cos（π-〈a，b〉）　　　 ＝λ|a||b|cos〈a，b〉＝λ（a·b）.当a，b中至少有一个是零向量或λ＝0时，显然也有（λa）·b＝λ（a·b）.当然，用同样的方法可以得到a·（λb）＝λ（a·b）.思考：向量的数量积满足结合律（a·b）·c＝a·（b·c）吗？提示：不满足.因为（a·b）·c表示一个与c共线的向量， a·（b·c）表示一个与a共线的向量，而c与a不一定共线，所以（a·b）·c ＝ a·（b·c）不一定成立. 当a，b，c中至少有一个是零向量时，分配律显然成立. 因此下面只要说明a，b，c都不是零向量的情形即可.     向量数量积的常用结论:   一　平面向量数量积的计算常考题型例1 已知|a|＝6，|b|＝5，当：（1）a∥b；（2）a⊥b；（3）a与b的夹角为60°时，分别求a与b的数量积.1.向量数量积的基本计算   C    C   二、向量的夹角问题  B     2.已知e1与e2是两个互相垂直的单位向量，求k为何值时，向量e1+ke2与ke1+e2的夹角为锐角.【解】因为e1+ke2与ke1+e2的夹角为锐角，所以（e1+ke2）·（ke1+e2）＝ke21+ke22+（k2+1）e1·e2＝2k>0，所以k>0.但当k＝1时，e1+ke2＝ke1+e2，它们的夹角为0°，不符合题意，舍去.综上，k的取值范围为k>0且k≠1.  三、向量的模的问题  1.模的计算  C  D 2.模的最值   ◆模的最值的转化方法求向量模的最值时，一般需要将模平方，转化为基向量的数量积，研究数量积在共线同向或共线反向时的取值.亦可结合图形，直观分析取得最值的位置.     四、向量的投影例7 ［2019·福建龙岩高一检测］已知向量a，b，其中|a|＝1，|a-2b|＝4，|a+2b|＝2，则a在b上的投影的数量为（　　）A.-1 B.1 C.-2 D.2【答案】　A    B       B D  六、数量积与平面几何问题 ◆利用向量判断三角形、四边形的形状的思路判断三角形或四边形的形状时，一般是由边长和角的关系来进行判断，充分利用向量的数量积公式寻求图形的边角关系，向量数量积为零意味着垂直关系成立，向量相等意味着线段平行且向量的模相等.D    2.利用数量积证明或求范围例10 如图所示，在四边形ABCD中，AB＝CD，但不平行，点M，N分别是AD，BC的中点，MN与BA，CD的延长线分别交于点P，Q，求证：∠APM＝∠DQM.◆利用向量数量积解决平面几何问题的步骤（1）用向量表示几何关系；（2）进行向量运算；（3）还原为几何结论. DA ◆解决与数量积最值（范围）有关问题的基本方法先进行数量积的有关运算，将数量积的最值（范围）转化为函数的最值（范围）问题，利用求函数最值（范围）的基本方法求出相关的最大值或最小值（或范围）.1.两个向量的夹角  2.向量的数量积    3.向量的投影 （2）向量投影的数量：一般地，如果a，b都是非零向量，则称|a|cos〈a，b〉为向量a在向量b上的投影的数量.注意：投影的数量与投影的长度有关，但是投影的数量既可能是非负数，也可能是负数.