2022-2023学年北京市丰台区七年级（上）期末数学试卷

这是一份2022-2023学年北京市丰台区七年级（上）期末数学试卷，共20页。试卷主要包含了填空题，解答题解答应写出文字说明等内容，欢迎下载使用。
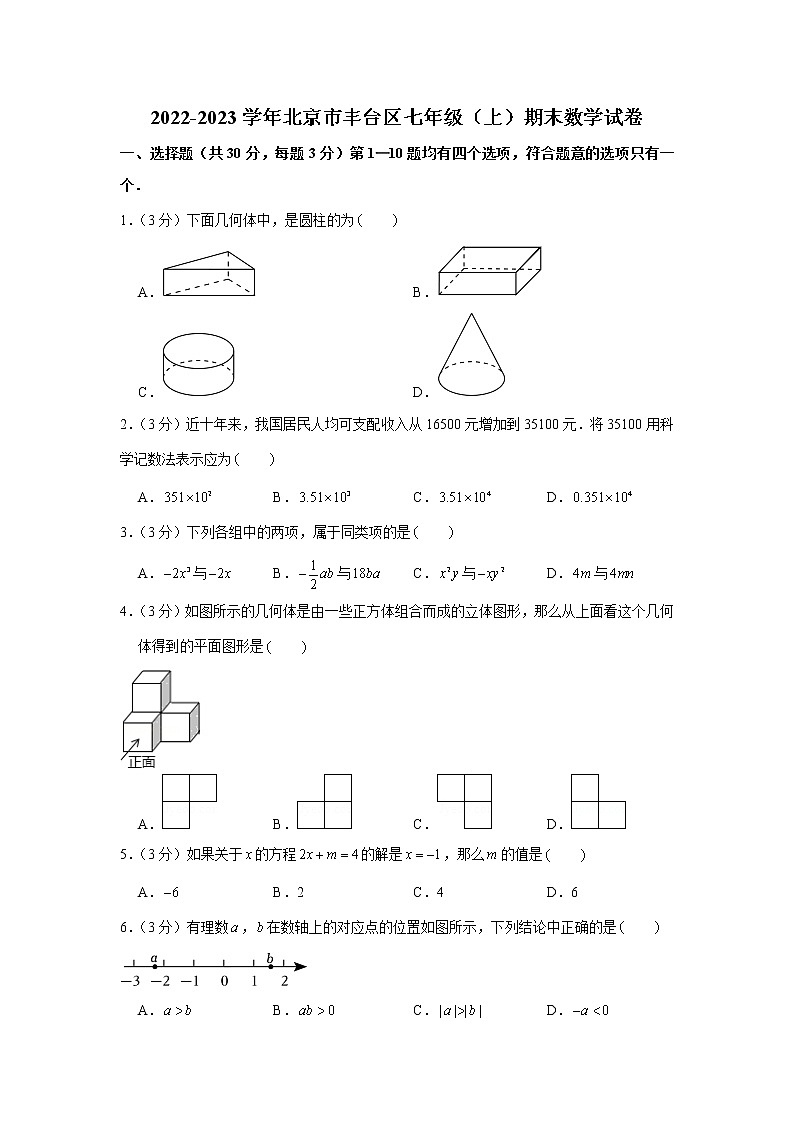
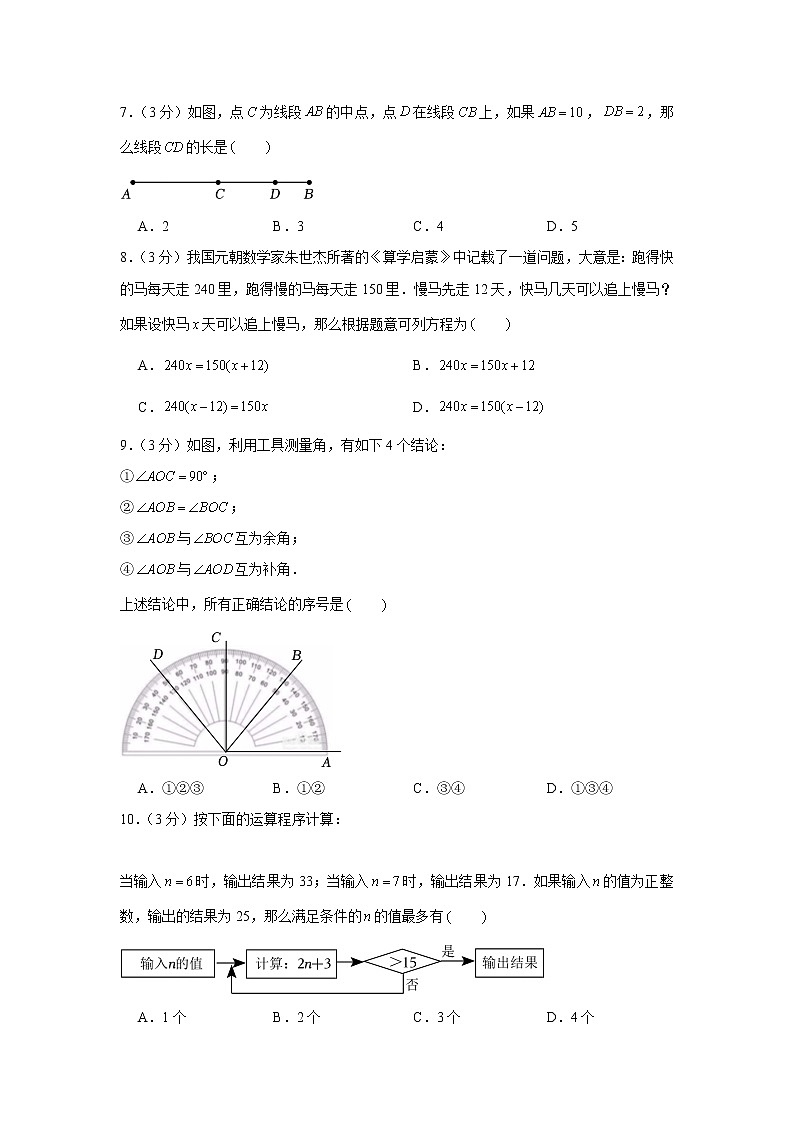
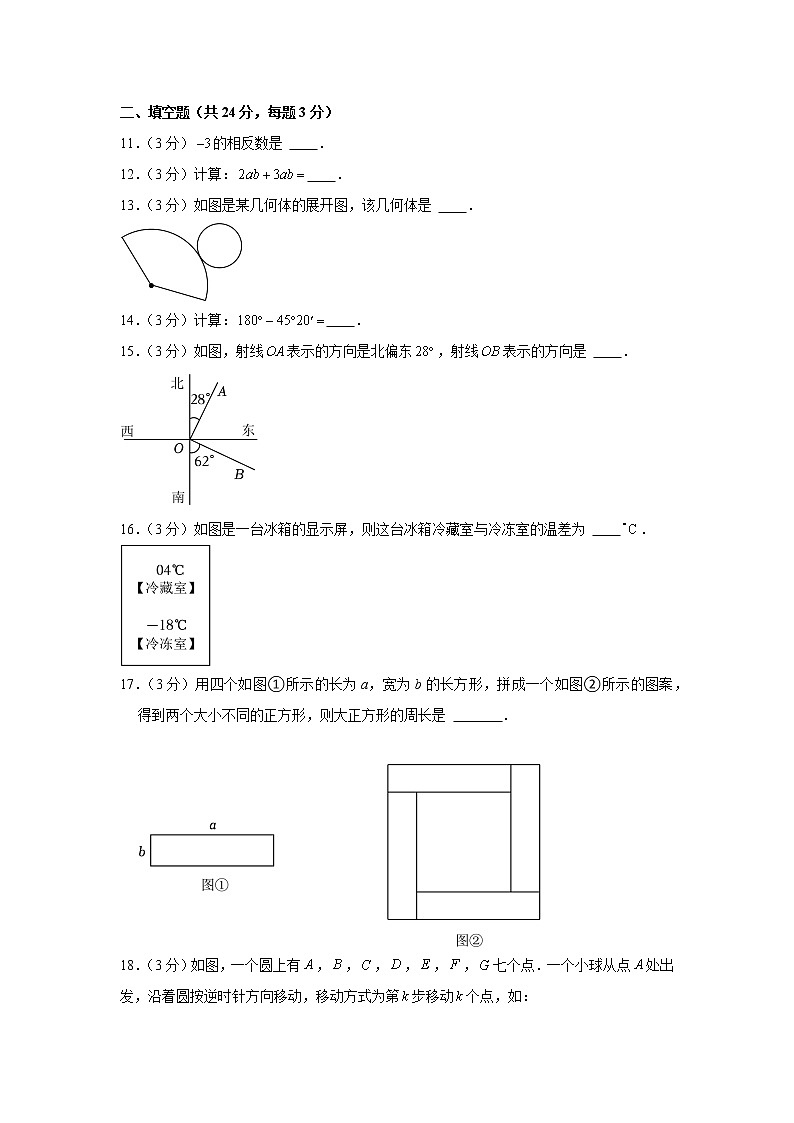
2022-2023学年北京市丰台区七年级（上）期末数学试卷一、选择题（共30分，每题3分）第1—10题均有四个选项，符合题意的选项只有一个．1．（3分）下面几何体中，是圆柱的为　　A． B． C． D．2．（3分）近十年来，我国居民人均可支配收入从16500元增加到35100元．将35100用科学记数法表示应为　　A． B． C． D．3．（3分）下列各组中的两项，属于同类项的是　　A．与 B．与 C．与 D．与4．（3分）如图所示的几何体是由一些正方体组合而成的立体图形，那么从上面看这个几何体得到的平面图形是　　A． B． C． D．5．（3分）如果关于的方程的解是，那么的值是　　A． B．2 C．4 D．66．（3分）有理数，在数轴上的对应点的位置如图所示，下列结论中正确的是　　A． B． C． D．7．（3分）如图，点为线段的中点，点在线段上，如果，，那么线段的长是　　A．2 B．3 C．4 D．58．（3分）我国元朝数学家朱世杰所著的《算学启蒙》中记载了一道问题，大意是：跑得快的马每天走240里，跑得慢的马每天走150里．慢马先走12天，快马几天可以追上慢马？如果设快马天可以追上慢马，那么根据题意可列方程为　　A． B． C． D．9．（3分）如图，利用工具测量角，有如下4个结论：①；②；③与互为余角；④与互为补角．上述结论中，所有正确结论的序号是　　A．①②③ B．①② C．③④ D．①③④10．（3分）按下面的运算程序计算： 当输入时，输出结果为33；当输入时，输出结果为17．如果输入的值为正整数，输出的结果为25，那么满足条件的的值最多有　　A．1个 B．2个 C．3个 D．4个二、填空题（共24分，每题3分）11．（3分）的相反数是 　　．12．（3分）计算：　　．13．（3分）如图是某几何体的展开图，该几何体是 　　．14．（3分）计算：　　．15．（3分）如图，射线表示的方向是北偏东，射线表示的方向是 　　．16．（3分）如图是一台冰箱的显示屏，则这台冰箱冷藏室与冷冻室的温差为 　　．17．（3分）用四个如图①所示的长为a，宽为b的长方形，拼成一个如图②所示的图案，得到两个大小不同的正方形，则大正方形的周长是 　   　． 18．（3分）如图，一个圆上有，，，，，，七个点．一个小球从点处出发，沿着圆按逆时针方向移动，移动方式为第步移动个点，如：第1步，从点处移动至点处；第2步，从点处移动至点处；第3步，从点处移动至点处；则第5步小球移动至点 　　处；第100步小球移动至点 　　处．三、解答题（共46分，第19题3分，第20-22题，每题4分，第23-27题，每题5分，第28题6分）解答应写出文字说明、演算步骤或证明过程。19．（3分）计算：．20．（4分）计算：．21．（4分）解方程：．22．（4分）解方程：．23．（5分）先化简，再求值：，其中，．24．（5分）如图，平面上有三个点，，．（1）根据下列语句按要求画图．①画直线，画射线，连接；②用圆规在线段的延长线上截取，连接（保留作图痕迹）；（2）　　（填“”“ ”或“” ，依据是 　　．25．（5分）如图，是直线上一点，平分，，．求的度数．补充完成下面的解答过程．解：因为是直线上一点，所以．因为平分，所以　　，所以与互为余角．因为，所以 　　与 　　互为余角．所以（依据是：　　．因为，所以　　．26．（5分）某学校在七年级开展种植类的劳动课程．现需要购买仿生阳光房若干个．经调查发现，同一款式的仿生阳光房在甲、乙两家商店的标价均是100元．新年将至，两家商店开展促销活动，优惠方式如下：甲商店：每个仿生阳光房按9折（标价的出售；乙商店：购买的仿生阳光房的个数不超过10时，按标价出售；购买的仿生阳光房的个数超过10时，超过部分按8折（标价的出售．（1）若在甲商店购买10个该款式的仿生阳光房，则花费 　　元；（2）若在乙商店购买个该款式的仿生阳光房，则花费 　　元（用含的代数式表示）；（3）购买该款式的仿生阳光房的个数为多少时，在甲、乙两家商店的花费相同？27．（5分）有这样一个问题：将一个两位数的十位上的数与个位上的数交换位置，得到一个新数，那么这个新数与原数的和能被11整除吗？下面是小明的探究过程，请补充完整：（1）举例：例①，；例②，；例③　　．（2）说理：设一个两位数的十位上的数是，个位上的数是，那么这个两位数可表示为 　　．依题意得到的新数可表示为 　　．通过计算说明这个两位数与得到的新数的和能否被11整除：　　．（3）结论：将一个两位数的十位上的数与个位上的数交换位置，得到一个新数，那么这个新数与原数的和 　　（填“能”或“不能” 被11整除．28．（6分）在数轴上，点表示的数为0，点表示的数为．给出如下定义：对于该数轴上的一点与线段上一点，如果线段的长度有最大值，那么称这个最大值为点与线段的“闭距离”．如图1，若，点表示的数为3，当点与点重合时，线段的长最大，值是4，则点与线段的“闭距离”为4．（1）如图2，在该数轴上，点表示的数为，点表示的数为2．①当时，点与线段的“闭距离”为 　　；②若点与线段的“闭距离”为3，求的值；（2）在该数轴上，点表示的数为，点表示的数为，若线段上存在点，使得点与线段的“闭距离”为4，直接写出的最大值与最小值．
2022-2023学年北京市丰台区七年级（上）期末数学试卷参考答案与试题解析一、选择题（共30分，每题3分）第1—10题均有四个选项，符合题意的选项只有一个．1．（3分）下面几何体中，是圆柱的为　　A． B． C． D．【解答】解：由图可知：是三棱柱，是四棱柱，是圆柱，是圆锥，故选：．2．（3分）近十年来，我国居民人均可支配收入从16500元增加到35100元．将35100用科学记数法表示应为　　A． B． C． D．【解答】解：．故选：．3．（3分）下列各组中的两项，属于同类项的是　　A．与 B．与 C．与 D．与【解答】解：．与所含字母相同，但相同字母的指数不相同，不是同类项，选项不符合题意；．与所含字母相同，并且相同字母的指数也相同，是同类项，选项符合题意；．与所含字母相同，但相同字母的指数不相同，不是同类项，选项不符合题意；．与所含字母不相同，不是同类项，选项不符合题意；故选：．4．（3分）如图所示的几何体是由一些正方体组合而成的立体图形，那么从上面看这个几何体得到的平面图形是　　A． B． C． D．【解答】解：根据几何体可得此图形的俯视图从左往右有2列，正方形的个数依次为2，1．故选：．5．（3分）如果关于的方程的解是，那么的值是　　A． B．2 C．4 D．6【解答】解：将代入原方程得，解得：，的值为6．故选：．6．（3分）有理数，在数轴上的对应点的位置如图所示，下列结论中正确的是　　A． B． C． D．【解答】解：由数轴可知，，，，，，，故选项不符合题意，只有选项是符合题意．故选：．7．（3分）如图，点为线段的中点，点在线段上，如果，，那么线段的长是　　A．2 B．3 C．4 D．5【解答】解：，是的中点，，．故选：．8．（3分）我国元朝数学家朱世杰所著的《算学启蒙》中记载了一道问题，大意是：跑得快的马每天走240里，跑得慢的马每天走150里．慢马先走12天，快马几天可以追上慢马？如果设快马天可以追上慢马，那么根据题意可列方程为　　A． B． C． D．【解答】解：设快马天可以追上慢马，则此时慢马已出发天，依题意，得：．故选：．9．（3分）如图，利用工具测量角，有如下4个结论：①；②；③与互为余角；④与互为补角．上述结论中，所有正确结论的序号是　　A．①②③ B．①② C．③④ D．①③④【解答】解：①，故①正确；②，，，故②不正确；③，与互为余角，故③正确；④，，，与互为补角，故④正确；所以，上述结论中，所有正确结论的序号是①③④，故选：．10．（3分）按下面的运算程序计算： 当输入时，输出结果为33；当输入时，输出结果为17．如果输入的值为正整数，输出的结果为25，那么满足条件的的值最多有　　A．1个 B．2个 C．3个 D．4个【解答】解：如果输入的值，一次运算就输出结果25，于是，解得；如果输入的值，两次运算才能输出结果25，于是第1次运算输出的结果为11，再第1次输入的数满足，解得；如果输入的值，三次运算才能输出结果25，于是第1次运算输出的结果为4，再第1次输入的数满足，解得不合题意舍去；所以满足条件的的值最多由2个，故选：．二、填空题（共24分，每题3分）11．（3分）的相反数是 　3　．【解答】解：，故的相反数是3．故答案为：3．12．（3分）计算：　　．【解答】解：原式．故答案为：．13．（3分）如图是某几何体的展开图，该几何体是 　圆锥　．【解答】解：由题意知，该几何体是圆锥，故答案为：圆锥．14．（3分）计算：　　．【解答】解：原式，故答案为：．15．（3分）如图，射线表示的方向是北偏东，射线表示的方向是 　南偏东　．【解答】解：根据方向角的定义可知，射线表示的方向是北偏东，射线表示的方向是南偏东，故答案为：南偏东．16．（3分）如图是一台冰箱的显示屏，则这台冰箱冷藏室与冷冻室的温差为 　22　．【解答】解：，故答案为：22．17．（3分）用四个如图①所示的长为a，宽为b的长方形，拼成一个如图②所示的图案，得到两个大小不同的正方形，则大正方形的周长是 　4a+4b　． 【解答】解：由题意可得，大正方形的边长为a+b，∴大正方形的周长＝4（a+b）＝4a+4b，故答案为：4a+4b．18．（3分）如图，一个圆上有，，，，，，七个点．一个小球从点处出发，沿着圆按逆时针方向移动，移动方式为第步移动个点，如：第1步，从点处移动至点处；第2步，从点处移动至点处；第3步，从点处移动至点处；则第5步小球移动至点 　　处；第100步小球移动至点 　　处．【解答】解：由题意知，前1步移动的点数为1，前2步移动的点数为，前3步移动的点数为，前4步移动的点数为，前步移动的点数为，前5步小球移动的点数为，前100步小球移动的点数为，由题意可知，当小球每移动1个点，2个点，3个点，4个点，5点点，6个点，7个点次到点、、、、、、处，，，第5步小球移动至点处；第100步小球移动至点处．故答案为：；．三、解答题（共46分，第19题3分，第20-22题，每题4分，第23-27题，每题5分，第28题6分）解答应写出文字说明、演算步骤或证明过程。19．（3分）计算：．【解答】解：原式．20．（4分）计算：．【解答】解：．21．（4分）解方程：．【解答】解：，，，，．22．（4分）解方程：．【解答】解：，去分母，得，去括号，得，移项，得，合并同类项，得．23．（5分）先化简，再求值：，其中，．【解答】解：；当，时，原式．24．（5分）如图，平面上有三个点，，．（1）根据下列语句按要求画图．①画直线，画射线，连接；②用圆规在线段的延长线上截取，连接（保留作图痕迹）；（2）　　（填“”“ ”或“” ，依据是 　　．【解答】解：（1）①如图，直线，射线，线段即为所求；②如图，线段即为所求．（2）．故答案为：．两点之间线段最短．25．（5分）如图，是直线上一点，平分，，．求的度数．补充完成下面的解答过程．解：因为是直线上一点，所以．因为平分，所以　90　，所以与互为余角．因为，所以 　　与 　　互为余角．所以（依据是：　　．因为，所以　　．【解答】解：是直线上一点，．平分，，与互为余角．，与互为余角．（依据是：同角的余角相等）．，．故答案为：90，，，同角的余角相等，30．26．（5分）某学校在七年级开展种植类的劳动课程．现需要购买仿生阳光房若干个．经调查发现，同一款式的仿生阳光房在甲、乙两家商店的标价均是100元．新年将至，两家商店开展促销活动，优惠方式如下：甲商店：每个仿生阳光房按9折（标价的出售；乙商店：购买的仿生阳光房的个数不超过10时，按标价出售；购买的仿生阳光房的个数超过10时，超过部分按8折（标价的出售．（1）若在甲商店购买10个该款式的仿生阳光房，则花费 　900　元；（2）若在乙商店购买个该款式的仿生阳光房，则花费 　　元（用含的代数式表示）；（3）购买该款式的仿生阳光房的个数为多少时，在甲、乙两家商店的花费相同？【解答】解：（1）（元，在甲商店购买10个该款式的仿生阳光房需花费900元，故答案为：900．（2）元，在乙商店购买个该款式的仿生阳光房需花费元，故答案为：．（3）当时，在甲、乙两家商店购买所需的费用不相等，根据题意得，解得，答：购买该款式的仿生阳光房20个时，在甲、乙两家商店的花费相同．27．（5分）有这样一个问题：将一个两位数的十位上的数与个位上的数交换位置，得到一个新数，那么这个新数与原数的和能被11整除吗？下面是小明的探究过程，请补充完整：（1）举例：例①，；例②，；例③　，　．（2）说理：设一个两位数的十位上的数是，个位上的数是，那么这个两位数可表示为 　　．依题意得到的新数可表示为 　　．通过计算说明这个两位数与得到的新数的和能否被11整除：　　．（3）结论：将一个两位数的十位上的数与个位上的数交换位置，得到一个新数，那么这个新数与原数的和 　　（填“能”或“不能” 被11整除．【解答】解：（1），，（答案不唯一）故答案为：，，（答案不唯一）（2）十位数字是，个位数字是的两位数可表示为：，交换后，十位数字是，个位数字是的两位数可表示为：，这两个两位数的和为：，而，所以这两个两位数的和能被11整除，故答案为：，，，；（3）由（1）（2）可知，将一个两位数的十位上的数与个位上的数交换位置，得到一个新数，那么这个新数与原数的和能被11整除，故答案为：能．28．（6分）在数轴上，点表示的数为0，点表示的数为．给出如下定义：对于该数轴上的一点与线段上一点，如果线段的长度有最大值，那么称这个最大值为点与线段的“闭距离”．如图1，若，点表示的数为3，当点与点重合时，线段的长最大，值是4，则点与线段的“闭距离”为4．（1）如图2，在该数轴上，点表示的数为，点表示的数为2．①当时，点与线段的“闭距离”为 　2　；②若点与线段的“闭距离”为3，求的值；（2）在该数轴上，点表示的数为，点表示的数为，若线段上存在点，使得点与线段的“闭距离”为4，直接写出的最大值与最小值．【解答】解：（1）①根据题意可知，时，到的最大值为的长，，，点与线段的“闭距离”为2，故答案为：2；②点到的“闭距离”为3，当时，，当时，，，的值为或5；（2）点表示的数为，点表示的数为，在线段上存在点，使得点与线段的“闭距离”为4，当时，可得不等式组，解得：，当时，可得不等式组，解得：，综上所述，或，的最大值为3，最小值为．