(新高考)高考数学一轮基础复习讲义5.1平面向量概念(2份打包，教师版+原卷版)

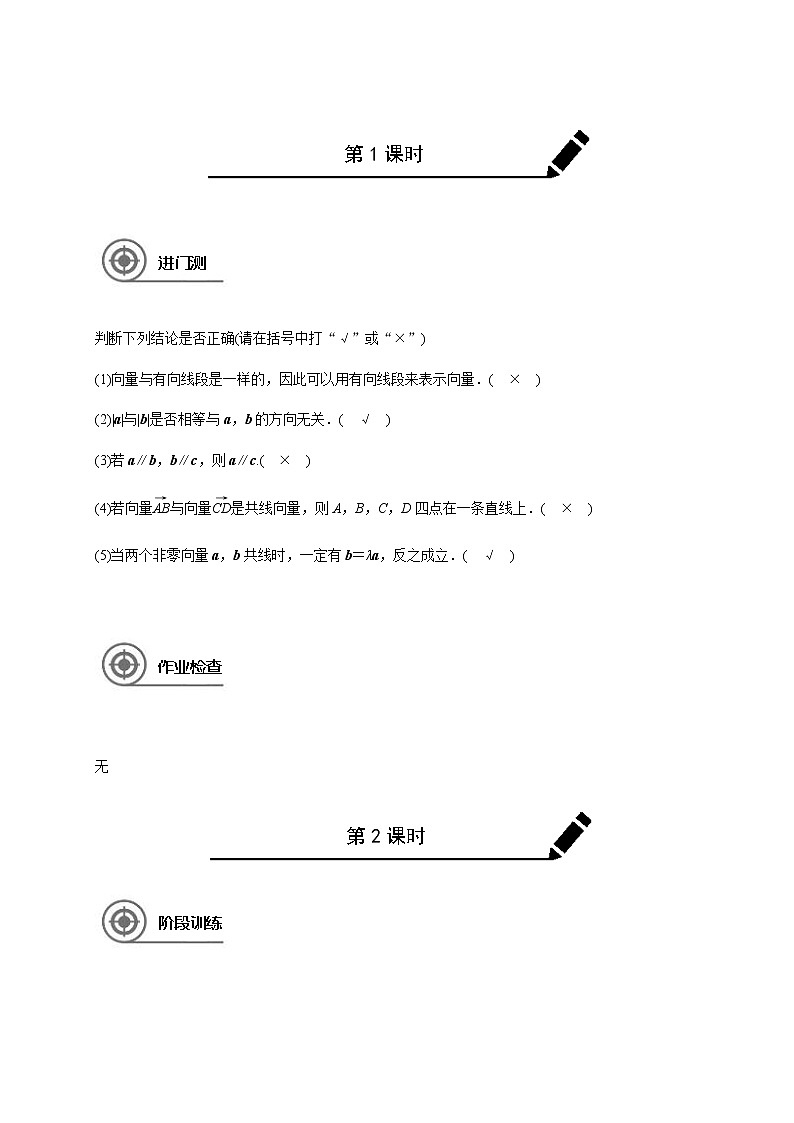
判断下列结论是否正确(请在括号中打“√”或“×”)

(1)向量与有向线段是一样的，因此可以用有向线段来表示向量．(　 　)

(2)|a|与|b|是否相等与a，b的方向无关．(　 　)

(3)若a∥b，b∥c，则a∥c.(　 　)

(4)若向量与向量是共线向量，则A，B，C，D四点在一条直线上．(　 　)

(5)当两个非零向量a，b共线时，一定有b＝λa，反之成立．(　 　)

无

题型一　平面向量的概念

例1　给出下列四个命题：

①若|a|＝|b|，则a＝b；

②若A，B，C，D是不共线的四点，则＝是四边形ABCD为平行四边形的充要条件；

③若a＝b，b＝c，则a＝c；

④a＝b的充要条件是|a|＝|b|且a∥b.

其中正确命题的序号是(　　)

A．②③   B．①②

C．③④   D．②④

题型二　平面向量的线性运算

命题点1　向量的线性运算

例2　(1)在平行四边形ABCD中，下列结论中错误的是(　　)

A.＝   B.＋＝

C.－＝   D.＋＝

(2)设D为△ABC所在平面内一点，若＝3，则(　　)

A.＝－＋   B.＝－

C.＝＋   D.＝－

命题点2　根据向量线性运算求参数

例3　(1)设D，E分别是△ABC的边AB，BC上的点，AD＝AB，BE＝BC.若＝λ1＋λ2(λ1，λ2为实数)，则λ1＋λ2的值为________．

(2)在△ABC中，点D在线段BC的延长线上，且＝3，点O在线段CD上(与点C，D不重合)，若＝x＋(1－x)，则x的取值范围是(　　)

A.   B.

C.   D.

　如图，一直线EF与平行四边形ABCD的两边AB，AD分别交于E，F两点，且交对角线AC于点K，其中，＝，＝，＝λ，则λ的值为(　　)

A.   B.

C.   D.

题型三　共线定理的应用

例4　设两个非零向量a与b不共线．

(1)若＝a＋b，＝2a＋8b，＝3(a－b)，

求证：A，B，D三点共线；

(2)试确定实数k，使ka＋b和a＋kb共线．

　(1)已知向量＝a＋3b，＝5a＋3b，＝－3a＋3b，则(　　)

A．A，B，C三点共线   B．A，B，D三点共线

C．A，C，D三点共线   D．B，C，D三点共线

(2)如图所示，设O是△ABC内部一点，且＋＝－2，则△ABC与△AOC的面积之比为________．

1．向量的有关概念

2.向量的线性运算

3.共线向量定理

向量a(a≠0)与b共线，当且仅当有唯一一个实数λ，使b＝λa.

【知识拓展】

1．一般地，首尾顺次相接的多个向量的和等于从第一个向量起点指向最后一个向量终点的向量，即＋＋＋…＋＝，特别地，一个封闭图形，首尾连接而成的向量和为零向量．

2．若P为线段AB的中点，O为平面内任一点，则＝(＋)．

3.＝λ＋μ(λ，μ为实数)，若点A，B，C共线，则λ＋μ＝1.

典例　下列叙述错误的是________．

①若a∥b，b∥c，则a∥c.

②若非零向量a与b方向相同或相反，则a＋b与a，b之一的方向相同．

③|a|＋|b|＝|a＋b|⇔a与b方向相同．

④向量b与向量a共线的充要条件是有且只有一个实数λ，使得b＝λa.

⑤＋＝0.

⑥若λa＝λb，则a＝b.

1．给出下列命题：①零向量的长度为零，方向是任意的；②若a，b都是单位向量，则a＝b；③向量与相等．则所有正确命题的序号是(　　)

A．①   B．③

C．①③   D．①②

2．D是△ABC的边AB上的中点，则向量等于(　　)

A．－＋   B．－－

C.－   D.＋

3．已知a，b是不共线的向量，＝λa＋b，＝a＋μb(λ，μ∈R)，那么A，B，C三点共线的充要条件是(　　)

A．λ＋μ＝2   B．λ－μ＝1

C．λμ＝－1   D．λμ＝1

4．在平行四边形ABCD中，对角线AC与BD交于点O，＋＝λ，则λ＝________.

1．设O是正方形ABCD的中心，则向量，，，是(　　)

A．相等的向量   B．平行的向量

C．有相同起点的向量   D．模相等的向量

2．在四边形ABCD中，AB∥CD，AB＝3DC，E为BC的中点，则等于(　　)

A.＋   B.＋

C.＋   D.＋

3．已知＝a＋2b，＝－5a＋6b，＝7a－2b，则下列一定共线的三点是(　　)

A．A，B，C   B．A，B，D

C．B，C，D   D．A，C，D

4．已知平面内一点P及△ABC，若＋＋＝，则点P与△ABC的位置关系是(　　)

A．点P在线段AB上   B．点P在线段BC上

C．点P在线段AC上   D．点P在△ABC外部

5. 如图所示，在△ABC中，点O是BC的中点，过点O的直线分别交直线AB，AC于不同的两点M，N，若＝m，＝n，则m＋n的值为(　　)

A．1   B．2

C．3   D．4

6．设P为锐角△ABC的外心(三角形外接圆的圆心)，＝k(＋)(k∈R)，若cos∠BAC＝，则k等于(　　)

A.  B.  C.  D.

7.如图，网格纸上小正方形的边长为1，若起点和终点均在格点的向量a，b，c满足c＝xa＋yb(x，y∈R)，则x＋y＝________.

8．设a，b不共线，＝2a＋pb，＝a＋b，＝a－2b，若A，B，D三点共线，则实数p的值是________．

*9.设G为△ABC的重心，且sin A·＋sin B·＋sin C·＝0，则角B的大小为________．

*10.已知△ABC和点M满足＋＋＝0.若存在实数m，使得＋＝m成立，则m＝________.

11．已知O为△ABC内一点，且满足＋λ＋(λ－1)＝0，若△OAB的面积与△OAC的面积的比值为，则λ的值为________．

12. 在△ABC中，D，E分别为BC，AC边上的中点，G为BE上一点，且GB＝2GE，设＝a，＝b，试用a，b表示，.

*13. 如图，在平行四边形ABCD中，O是对角线AC，BD的交点，N是线段OD的中点，AN的延长线与CD交于点E，若＝m＋，求实数m的值．