数学八年级下册18.2.3 正方形精品精练

这是一份数学八年级下册18.2.3 正方形精品精练，文件包含2023年人教版数学八年级下册《正方形的性质与判定》专项练习含答案doc、2023年人教版数学八年级下册《正方形的性质与判定》专项练习原卷版doc等2份试卷配套教学资源，其中试卷共20页， 欢迎下载使用。
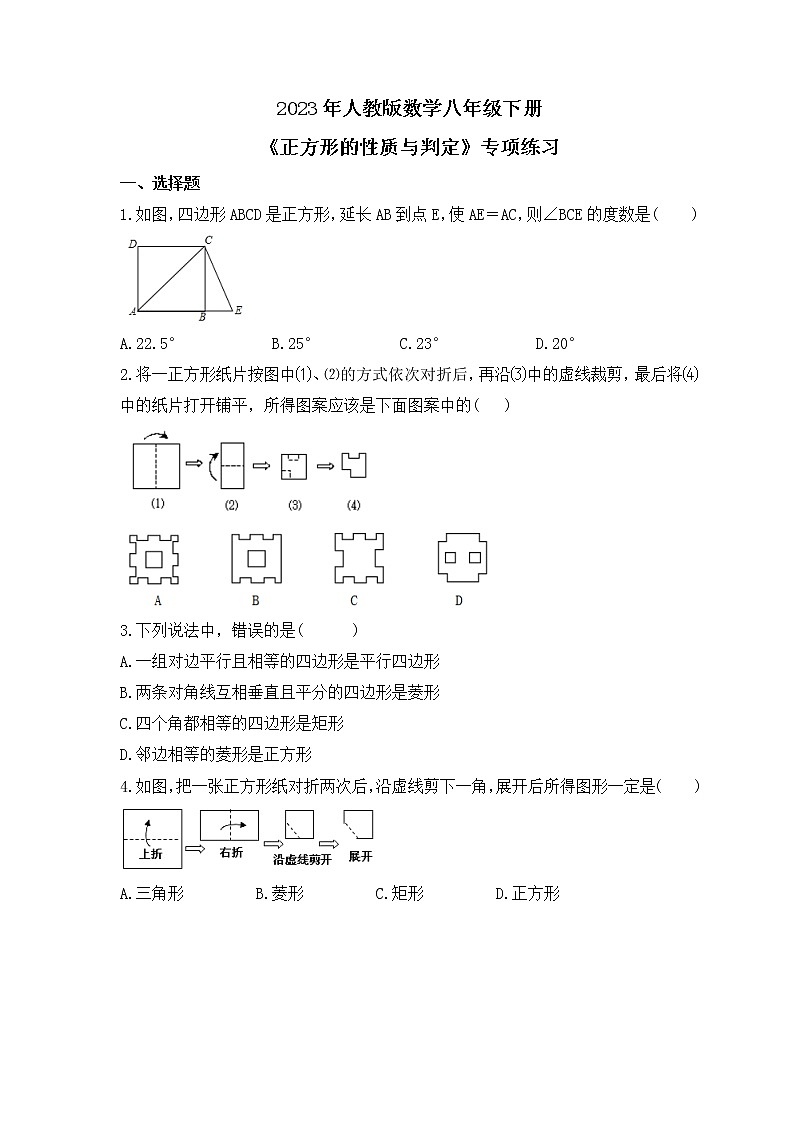
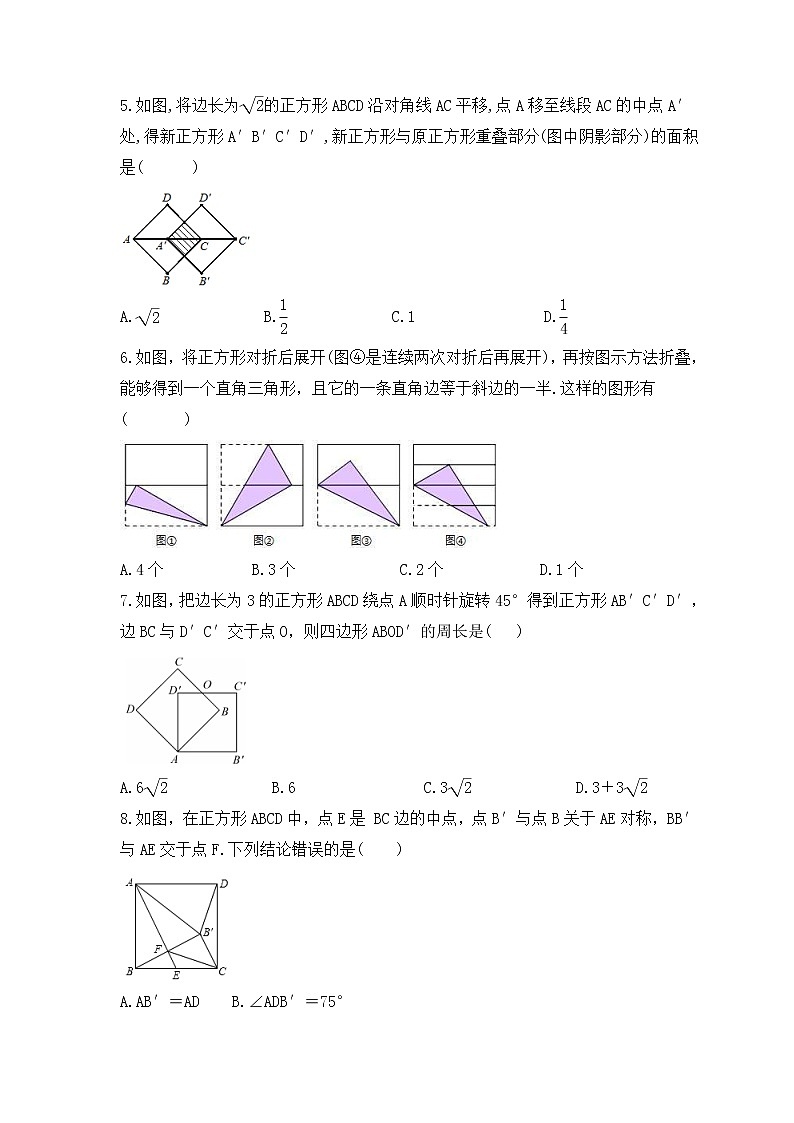
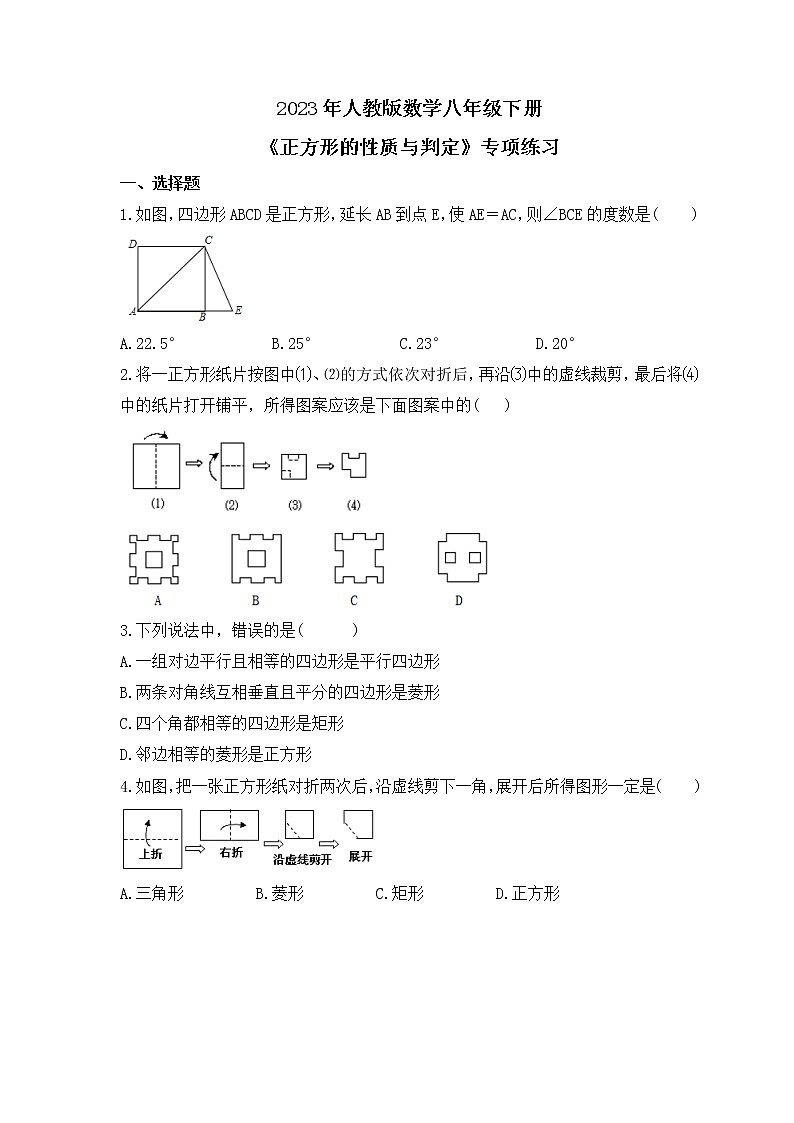
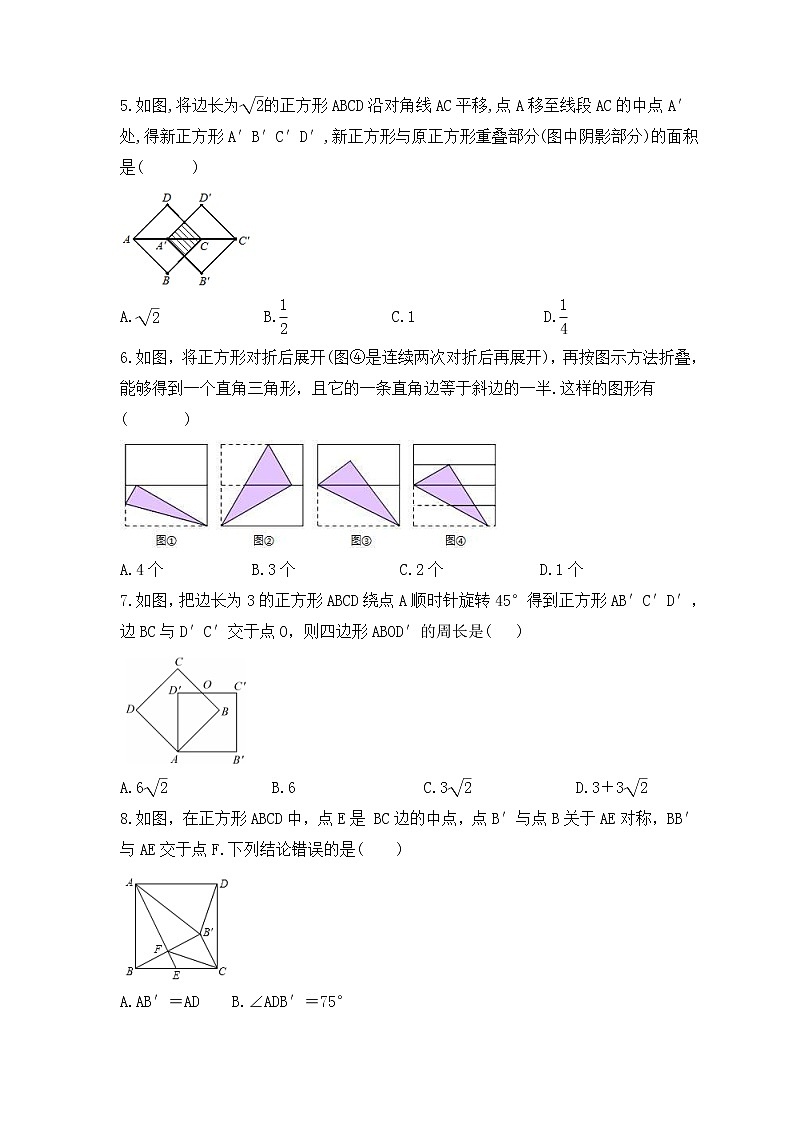
2023年人教版数学八年级下册《正方形的性质与判定》专项练习一              、选择题1.如图，四边形ABCD是正方形，延长AB到点E，使AE＝AC，则∠BCE的度数是(　　)A.22.5°         B.25°          C.23°           D.20°2.将一正方形纸片按图中⑴、⑵的方式依次对折后，再沿⑶中的虚线裁剪，最后将⑷中的纸片打开铺平，所得图案应该是下面图案中的(   )3.下列说法中，错误的是(      )A.一组对边平行且相等的四边形是平行四边形B.两条对角线互相垂直且平分的四边形是菱形C.四个角都相等的四边形是矩形D.邻边相等的菱形是正方形4.如图，把一张正方形纸对折两次后，沿虚线剪下一角，展开后所得图形一定是(　　)A.三角形         B.菱形         C.矩形         D.正方形  5.如图,将边长为的正方形ABCD沿对角线AC平移,点A移至线段AC的中点A′处,得新正方形A′B′C′D′,新正方形与原正方形重叠部分(图中阴影部分)的面积是(      )A.                           B.                           C.1                              D.6.如图，将正方形对折后展开(图④是连续两次对折后再展开)，再按图示方法折叠，能够得到一个直角三角形，且它的一条直角边等于斜边的一半.这样的图形有(    )A.4个      B.3个            C.2个        D.1个7.如图，把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′，边BC与D′C′交于点O，则四边形ABOD′的周长是(  )A.6             B.6                C.3             D.3＋38.如图，在正方形ABCD中，点E是 BC边的中点，点B′与点B关于AE对称，BB′与AE交于点F.下列结论错误的是(　　)A.AB′＝AD                  B.∠ADB′＝75°   C.∠CB′D＝135°                 D.△FCB′是等腰直角三角形9.如图，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD＋PE最小，则这个最小值为(　　)A.         B.2          C.2        D. 10.如图，P为正方形ABCD的对角线BD上任一点，过点P作PE⊥BC于点E，PF⊥CD于点F，连接EF.给出以下4个结论：①△FPD是等腰直角三角形；②AP＝EF；③AD＝PD；④∠PFE＝∠BAP.其中，所有正确的结论是(　　)A.①②          B.①④             C.①②④         D.①③④11.如图，ABCD是正方形场地，点E在DC的延长线上，AE与BC相交于点F.有甲、乙、丙三名同学同时从点A出发，甲沿着A→B→F→C的路径行走至C，乙沿着A→F→E→C→D的路径行走至D，丙沿着A→F→C→D的路径行走至D.若三名同学行走的速度都相同，则他们到达各自的目的地的先后顺序(由先至后)是(　　)A.甲乙丙       B.甲丙乙         C.乙丙甲       D.丙甲乙12.如图，正方形纸片ABCD，P为正方形AD边上的一点(不与点A，点D重合)，将正方形纸片折叠，使点B落在点P处，点C落在点G处，PG交DC于点H，折痕为EF，连接BP，BH.BH交EF于点M，连接PM.下列结论：①BE＝PE；②EF＝BP；③PB平分∠APG；④MH＝MF；⑤BP＝BM.其中正确结论的个数是(　　)A.5           B.4            C.3          D.2二              、填空题13.如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E．若∠CBF＝20°，则∠AED等于　　　　．14.如图，直线l过正方形ABCD的顶点D，过A、C分别作直线l的垂线，垂足分别为E、F.若AE＝4a，CF＝a，则正方形ABCD的面积为　   　.15.如图1，在边长为a的大正方形中剪去一个边长为b的小正方形，再将图中的阴影部分剪拼成一个长方形，如图2．这个拼成的长方形的长为30，宽为20．则图2中Ⅱ部分的面积是        ．16.如图为两正方形ABCD、CEFG和矩形DFHI的位置图，其中D，A两点分别在CG、BI上，若AB＝3，CE＝5，则矩形DFHI的面积是　   　.17.如图，线段AC＝n＋1(其中n为正整数)，点B在线段AC上，在线段AC同侧作正方形ABMN及正方形BCEF，连接AM、ME、EA得到△AME.当AB＝1时，△AME的面积记为S1；当AB＝2时，△AME的面积记为S2；当AB＝3时，△AME的面积记为S3；则S3﹣S2＝　   　.18.如图，在平面直角坐标系中，边长为1的正方形OA1B1C的对角线A1C和OB1交于点M1；以M1A1为对角线作第二个正方形A2A1B2 M1，对角线A1 M1和A2B2 交于点M2；以M2A1为对角线作第三个正方形A3A1B3 M2，对角线A1 M2和A3B3 交于点M3；……，依次类推，这样作的第n个正方形对角线交点的坐标为Mn________.三              、解答题19.已知：在正方形ABCD中，点G是BC边上的任意一点，DE⊥AG于点E，BF∥DE，交AG于点F. 求证：(1)△ADE≌△BAF；(2)AF＝BF＋EF. 20.如图，在正方形ABCD中，BC＝2，E是对角线BD上的一点，且BE＝AB.求△EBC的面积．     21.如图，点E、F分别在正方形ABCD的边DC、BC上，AG⊥EF，垂足为G，且AG＝AB，求∠EAF的度数.    22.如图：已知AD是△ABC的角平分线，DE∥AC交AB于E，DF∥AB交AC于F.(1)求证：四边形AEDF是菱形；(2)当△ABC满足什么条件时，四边形AEDF是正方形？   23.如图，在正方形ABCD内有一点P满足AP＝AB，PB＝PC，连接AC、PD.求证：(1)△APB≌△DPC；(2)∠BAP＝2∠PAC.       24.如图，正方形ABCD的对角线交于点O，点E，F分别在AB，BC上(AE＜BE)，且∠EOF＝90°，OE，DA的延长线交于点M，OF，AB的延长线交于点N，连接MN.(1)求证：OM＝ON；(2)若正方形ABCD的边长为4，E为OM的中点，求MN的长.         25.如图，四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去…(1)记正方形ABCD的边长为a1＝1，按上述方法所作的正方形的边长依次为a2，a3，a4，…，请求出a2，a3，a4的值；(2)根据上述规律写出an的表达式.
答案1.A2.B.3.D4.B.5.D6.C.7.A8.B；9.B10.C.11.B.12.B.13.答案为：65°.14.答案为：17a2.15.答案为：100.16.答案为：43.5.17.答案为：.18.答案为：.19.解：(1)由正方形的性质可知：AD＝AB，∵∠BAF＋∠ABF＝∠BAF＋∠DAE＝90°，∴∠ABF＝∠DAE，在△ADE与△BAF中，∴△ADE≌△BAF(AAS)(2)由(1)可知：BF＝AE，∴AF＝AE＋EF＝BF＋EF 20.解：作EF⊥BC于F，如图所示：则∠EFB＝90°，∵四边形ABCD是正方形，∴AB＝BC＝2，∠DAB＝∠ABC＝90°，∴∠ABD＝∠DBC＝∠ABC＝45°，∴△BEF是等腰直角三角形，∴EF＝BF，∵BE＝AB，∴BE＝BC＝2，∴EF＝BF＝BE＝，∴△EBC的面积＝BC•EF＝×2×＝．21.解：在Rt△ABF与Rt△AGF中，∵AB＝AG，AF＝AF，∠B＝∠G＝90°，∴△ABF≌△AGF(HL)，∴∠BAF＝∠GAF，同理易得：△AGE≌△ADE，有∠GAE＝∠DAE；即∠EAF＝∠EAG＋∠FAG＝∠DAG＋∠BAG＝∠DAB＝45°，故∠EAF＝45°.22.解：(1)证明：∵DE∥AC，DF∥AB，∴DE∥AF，DF∥AE，∴四边形AEDF是平行四边形(有两组对边相互平行的四边形是平行四边形)，∴∠EAF＝∠EDF(平行四边形的对角相等)；又∵AD是△ABC的角平分线，∴∠EAD＝∠EDA(平行四边形的对角线平分对角)，∴AE＝DE(等角对等边)，∴四边形AEDF是菱形(邻边相等的平行四边形是菱形)；(2)由(1)知，四边形AEDF是菱形，∵当四边形AEDF是正方形时，∠EAF＝90°，即∠BAC＝90°，∴△ABC的∠BAC＝90°时，四边形AEDF是正方形.23.证明：(1)∵四边形ABCD是正方形，∴∠ABC＝∠DCB＝90°.∵PB＝PC，∴∠PBC＝∠PCB.∴∠ABC﹣∠PBC＝∠DCB﹣∠PCB，即∠ABP＝∠DCP.又∵AB＝DC，PB＝PC，∴△APB≌△DPC.(2)证明：∵四边形ABCD是正方形，∴∠BAC＝∠DAC＝45°.∵△APB≌△DPC，∴AP＝DP.又∵AP＝AB＝AD，∴DP＝AP＝AD.∴△APD是等边三角形.∴∠DAP＝60°.∴∠PAC＝∠DAP﹣∠DAC＝15°.∴∠BAP＝∠BAC﹣∠PAC＝30°.∴∠BAP＝2∠PAC.24.解：(1)证明：正方形ABCD中，AC＝BD，OA＝AC，OB＝OD＝BD，所以OA＝OB＝OD，因为AC⊥BD，所以∠AOB＝∠AOD＝90°，所以∠OAD＝∠OBA＝45°，所以∠OAM＝∠OBN，又因为∠EOF＝90°，所以∠AOM＝∠BON，所以△AOM≌△BON，所以OM＝ON.(2)如图，过点O作OP⊥AB于P，所以∠OPA＝90°，∠OPA＝∠MAE，因为E为OM中点，所以OE＝ME，又因为∠AEM＝∠PEO，所以△AEM≌△PEO，所以AE＝EP，因为OA＝OB，OP⊥AB，所以AP＝BP＝AB＝2，所以EP＝1.Rt△OPB中，∠OBP＝45°，所以OP＝PB＝2，Rt△OEP中，OE＝，所以OM＝2OE＝2，Rt△OMN中，OM＝ON，所以MN＝OM＝2.25.解：(1)a2＝AC，且在直角△ABC中，AB2＋BC2＝AC2，∴a2＝a1＝，同理a3＝a2＝()2a1＝2，a4＝a3＝()3a1＝2；(2)由(1)结论可知：a2＝a1＝，a3＝a2＝()2a1＝2，a4＝a3＝()3a1＝2；…故找到规律an＝()n﹣1a1＝()n﹣1.