湘教版（2019）必修 第一册4.1 实数指数幂和幂函数公开课课件ppt

这是一份湘教版（2019）必修 第一册4.1 实数指数幂和幂函数公开课课件ppt，共22页。PPT课件主要包含了学习目标，①⑤⑥，即时巩固，随堂小测，课堂小结等内容，欢迎下载使用。

1.通过具体实例，结合函数 的图象，理解幂函数图象的变化规律.2.了解幂函数的概念.核心素养：数学抽象、数学建模、直观想象

【以下各个函数有什么共同的特征？】
【1】在函数① ② ③ ④ ⑤ ⑥ 中，是幂函数的是（ ） .
【解】根据幂函数的定义，只有①⑤⑥是幂函数. 选项②系数不为1；选项③系数不为1且多了常数项 选项④同理.
归纳总结 幂函数的特征
【1】 的系数为1
【2】 的底数为自变量
【3】 的指数为常数
只有同时满足这三个条件的，才是幂函数.形如 等的函数不是幂函数.
判断一个函数是不是幂函数的依据是该函数是否为 ( 为常数)的形式.反过来，若一个函数为幂函数，那么它也一定具有这个形式.在我们解决某些问题的时候这个结论有奇效.
【1】已知幂函数 的图像经过点 ，求这个函数的表达式.
【解】由题意设函数的表达式为
把点 代入，得：
即 ，所以
所以这个函数的表达式为
和初中解决一次函数一样，利用待定系数法.因为幂函数只有一个系数，所以只需要一个点的坐标就可以求写出幂函数的表达式.
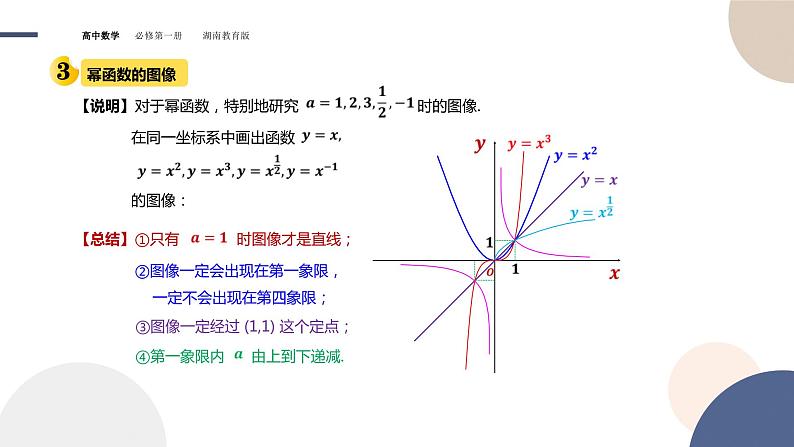
【说明】对于幂函数，特别地研究 时的图像.
在同一坐标系中画出函数
【总结】①只有 时图像才是直线；
②图像一定会出现在第一象限， 一定不会出现在第四象限；
③图像一定经过 (1,1) 这个定点；
④第一象限内 由上到下递减.
【总结】⑤ 时，图像在定义域内上升；
⑥ 时，图像在第一象限下降；
⑦只有 时，图像才与坐标轴 相交，且交点一定为原点；
⑧ 时，图像是y=1这条直线.
【说明】对于幂函数，特别地研究 时图像的性质.
【1】求幂函数 的定义域并讨论其奇偶性和单调性.
【解】因为 ， ，又 为 两个连续的正整数相乘，其结果必为正偶数，所以 为正奇数，所以函数的定义域为R.
由 为正奇数，得
，所以 为增函数.
因为 ，所以 是正的奇次方根，所以 在定义域内为增函数.
和 两种情况下幂函数的图像变化及性质表：
在(0，+∞)上都有定义，定义域与a的取值有关
图像过点(0，0)和点(1，1)
在(0，+∞)上是增函数
在(0，+∞)上是减函数
在第一象限，当0＜a＜1时，图像上凸；当a＞1时，图像下凹
在第一象限，图像都下凹
【2】利用幂函数的性质，比较下列两个数的大小.
【解】设 ，则 在R上为增函数.
比较大小用作差法.由增减性，根据自变量的大小，比较函数值的大小；或者根据函数值的大小，比较自变量的大小.
∵ -1.5＜-1.4，∴ (-1.5)3＜(-1.4)3
(-1.5)3 和 (-1.4)3
幂函数 奇偶性的判断方法
【例题】证明幂函数 是增函数.
【证明】函数的定义域是[0，+∞).
因为 ， ，所以
即幂函数 是增函数.
2.以下结论正确的是A.当α＝0时，函数y＝xα的图象是一条直线B.幂函数的图象都经过(0,0)，(1,1)两点C.若幂函数y＝xα的图象关于原点对称，则y＝xα在定义域内y随x的增 大而增大D.幂函数的图象不可能在第四象限，但可能在第二象限
A.1,3 B.－1,1 C.－1,3 D.－1,1,3
4.若a<0，则0.5a,5a,5－a的大小关系是A.5－a<5a<0.5a B.5a<0.5a<5－<5－a<5a D.5a<5－a<0.5a
所以5a<0.5a<5－a.
5.先分析函数 的性质，再画出其图象.