



还剩25页未读,
继续阅读
沪科版数学九年级下册 24.2 第1课时 与圆有关的概念及点与圆的位置关系 课件
展开
这是一份沪科版数学九年级下册 24.2 第1课时 与圆有关的概念及点与圆的位置关系 课件,共33页。
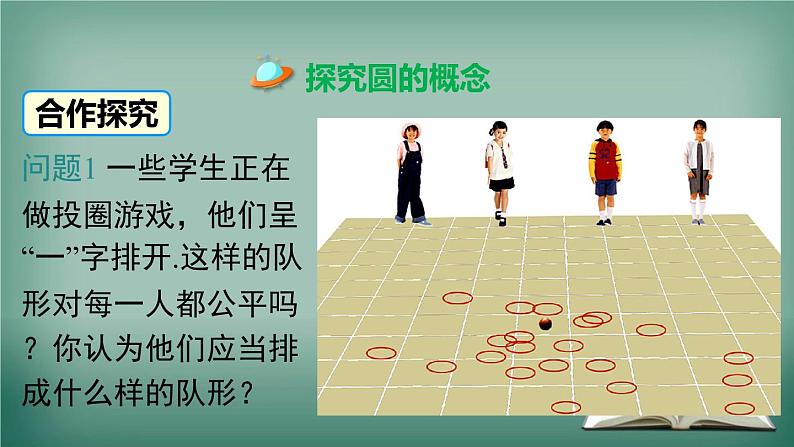
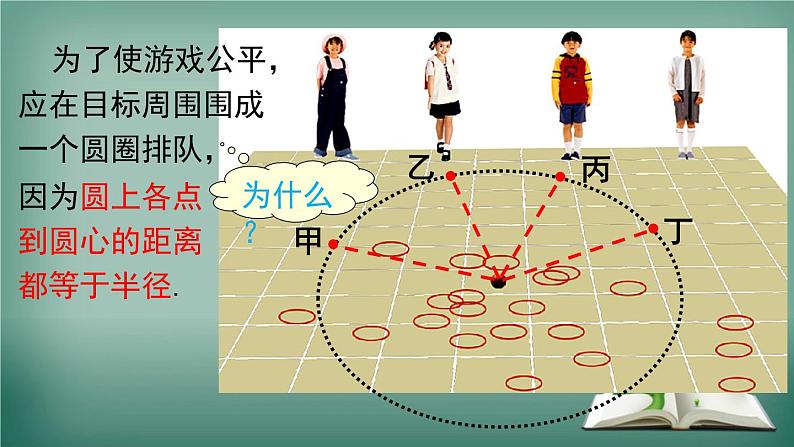
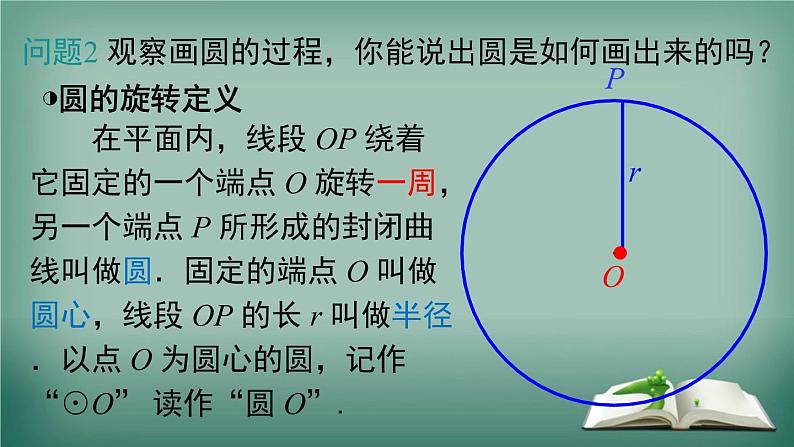
24.2 圆的基本性质第1课时 与圆有关的概念及点与圆的位置关系第24章 圆观察下列生活中的图片,找一找你所熟悉的图形.图片引入骑车运动看了此画,你有何想法?问题1 一些学生正在做投圈游戏,他们呈“一”字排开.这样的队形对每一人都公平吗?你认为他们应当排成什么样的队形?探究圆的概念合作探究甲丙乙丁为了使游戏公平,应在目标周围围成一个圆圈排队,因为圆上各点到圆心的距离都等于半径.为什么?·rOP◑圆的旋转定义 在平面内,线段 OP 绕着它固定的一个端点 O 旋转一周,另一个端点 P 所形成的封闭曲线叫做圆.固定的端点 O 叫做圆心,线段 OP 的长 r 叫做半径.以点 O 为圆心的圆,记作“⊙O” 读作“圆 O”.问题2 观察画圆的过程,你能说出圆是如何画出来的吗? 一是圆心,圆心确定其位置;二是半径,半径确定其大小.半径相同,圆心不同圆心相同,半径不同◑确定一个圆的要素(1) 圆上各点到定点 (圆心 O) 的距离都等于 .(2) 平面内到定点 (圆心 O) 的距离等于定长 (半径 r) 的所 有点都在 . 由此,我们可以得到圆的集合定义:平面内到定点 (圆心 O) 的距离等于定长 (半径 r) 的所有点组成的图形.Orrrrr定长(半径 r)同一个圆上想一想:从画圆的过程可以看出什么呢?·例1 如图,已知 AB,CD 为⊙O 的直径. 求证:AD∥CB. 典例精析证明:连接 AC,DB.∵ AB,CD 为⊙O 的直径,∴ OA = OB, OC = OD.∴ 四边形 ADBC 为平行四边形.∴ AD∥CB.ABCDO矩形 ABCD 的对角线 AC、BD 相交于 O.求证:A、B、C、D 在以 O 为圆心的同一圆上.证明:∵四边形 ABCD 是矩形, ∴ ∴ A、B、C、D 在以 O 为圆心,以 OA 为半径的圆上.练一练问题1 观察下图中点和圆的位置关系有哪几种?.C.... B. A..有三种:点在圆内,点在圆上,点在圆外.点和圆的位置关系观察与思考问题2 设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系下,d与r有怎样的数量关系?点P在⊙O内 点P在⊙O上 点P在⊙O外 d d drPdd Prd<r r =>r 反过来,由 d 与 r 的数量关系,怎样判定点与圆的位置关系呢?1. ⊙O 的半径为 10 cm,A、B、C 三点到圆心的距离分 别为 8 cm、10 cm、12 cm,则点 A、B、C 与⊙O 的 位置关系是点 A 在 ;点 B 在 ;点 C 在 . 圆内圆上圆外2. 圆心为 O 的两个同心圆,半径分别为 1 和 2,若 OP = ,则点 P 在 ( ) A. 大圆内 B. 小圆内 C. 小圆外 D. 大圆内,小圆外D练一练点和圆的位置关系数形结合:位置关系数量关系知识要点例2 如图,已知矩形 ABCD 的边 AB = 3,AD = 4.(1)以 A 为圆心,4 为半径作⊙A,则点 B、C、D 与 ⊙A 的位置关系如何?解:∵AB = 3 < 4, ∴ 点 B 在⊙A 内. ∵ AD = 4, ∴ 点 D 在 ⊙A 上. ∵ > 4, ∴ 点 C 在 ⊙A 外.(2)若以 A 点为圆心作⊙A, 使 B、C、D 三点中至少 有一点在圆内,且至少 有一点在圆外,求⊙A 的半径 r 的取值范围.解:由题意得,点 B 一定在圆内,点 C 一定在圆外,∴ 3<r<5.【变式题】如图,在平面直角坐标系中,点 A 的坐标为 (2,1),P 是 x 轴上一点,要使 △PAO 为等腰三角形,满足条件的 P 有几个?求出点 P 的坐标.方法总结:在没有明确腰和底边的情况下,构造等腰三角形要注意分类讨论.◑弧: 圆的有关概念◑弦: 连接圆上任意两点的线段(如图中的 AB,AC)叫做弦. 经过圆心的弦(如图中的 AB)叫做直径.注意:1. 弦和直径都是线段;2. 直径是特殊的弦,它经过圆心,是圆中最长的弦,但弦不一定是直径.◑半圆、优弧及劣弧: 圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆.劣弧与优弧 ·COAB半圆◑等圆: 能够重合的两个圆叫做等圆,等圆的半径相等.◑等弧: 在同圆或等圆中,能够互相重合的弧叫做等弧.练一练 有下列五个说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆;⑤任意一条直径都是圆的对称轴.其中错误说法的个数是 ( ) A.1 B.2 C.3 D.4解析:根据圆、直径、弦、半圆等概念来判断.半径只能确定圆的大小,不能确定圆的位置;直径是弦,但弦不一定是直径;对称轴是直线,故应说任意一条直径所在的直线是圆的对称轴.故①③⑤错误.C1. 根据圆的定义,圆指的是“圆周”,而不是“圆面”;2. 直径是圆中最长的弦.证明: 连接 OC.在△AOC 中,根据三角形三边关系有 OA + OC > AC,而 AB = 2OA,OA = OC,∴ AB > AC.知识要点例 4 如图,AB 是⊙O 的直径,CD 是⊙O 的弦,AB,CD 的延长线交于点 E. 已知 AB = 2DE,∠E = 18°,求∠AOC 的度数.解:如图,连接 OD.∵ AB 是⊙O 的直径,OC,OD 是半径,AB = 2DE,∴OD = DE.∴∠DOE = ∠E = 18°.∴∠ODC = ∠DOE+∠E = 36°.∵ OC = OD,∴∠C = ∠ODC = 36°.∴∠AOC = ∠C+∠E = 36°+18° = 54°.例 5 如图,MN 是半圆 O 的直径,正方形 ABCD 的顶点 A、D 在半圆上,B、C 在 MN 上,求证:OB = OC.ⅠⅡ10?2x在 Rt△ABO 中,AB2 + BO2 = AO2,即 (2x)2 + x2 = 102.ABOCDMN算一算:设⊙O 的半径为 10,则正方形 ABCD 的边长为 . x连接 OA,OD,则OA = OD,由三角形全等可证 OB = OC.xxxx【变式题】如图,在扇形 MON 中,∠MON = 45°,半径 MO = NO = 10,正方形 ABCD 的顶点 B、C、D 在半径 上,顶点 A 在圆弧上,求正方形 ABCD 的边长.解:连接 OA,如图.又∵∠DOC = 45°,∴CD = OC.设 AB = x,则 AB = BC = DC = OC = x.∵OA = OM = 10,∴ (2x)2 + x2 = 102.在 Rt△ABO 中,在正方形 ABCD 中,AB = BC = CD,∠ABC =∠DCB = 90°.45°1. 判断下列说法的正误,并说明理由或举反例.(1) 弦是直径;(2) 半圆是弧;(3) 过圆心的线段是直径;(4) 过圆心的直线是直径;(5) 半圆是最长的弧;(6) 直径是最长的弦;(7) 长度相等的弧是等弧.2. 填空:(1)______是圆中最长的弦,它是______的 2 倍.(2)图中有 条直径, 条非直径的弦, 圆中以 A 为一个端点的优弧有 条, 劣弧有 条.直径半径1244 3. 正方形 ABCD 的边长为 2 cm,以 A 为圆心,2 cm 长为 半径作⊙A,则点 B 在⊙A ;点 C 在⊙A ;点 D 在⊙A .上外上4. 如图,MN 为⊙O 的弦,∠MON = 70°,则∠M = °.5. 一点到⊙O 上的最近距离为 4 cm,最远距离为 10 cm, 则这个圆的半径是 .7 cm 或 3 cm55·2 cm3 cm6. 画出由所有到已知点 O 的距离大于或等于 2 cm 并且 小于或等于 3 cm 的点组成的图形.O7. 如图,OA、OB 是⊙O 的半径,点 C、D 分别为 OA、 OB 的中点,求证:AD = BC.证明:∵ OA、OB 是⊙O 的半径,∴ OA = OB.∵ 点 C、D 分别为 OA、OB 的中点,∴ OA = 2OC,OB = 2OD.∴ OC = OD.又∵∠O =∠O,∴△AOD≌△BOC (SAS).∴ BC = AD.解:渔船应沿着射线 OP 的方向航行才能尽快离开危险区.理由如下:设射线 OP 交⊙O 于点 A,过点 P 任意作一条弦 CD,连接 OD. 在△ODP中,OD-OP<PD,又∵OD = OA,∴OA-OP<PD. ∴ PA<PD,即 PA 为最短路线,故渔船沿射线 OP 方向航行才能尽快离开危险区.能力提升:8. 如图,点 O 处有一灯塔,警示⊙O 内部为危险区,一 渔船误入危险区点 P 处,该渔船应该按什么方向航行 才能尽快离开危险区?试说明理由.ADPCO圆定义旋转定义集合定义有关概念直径是圆中最长的弦弧半圆是特殊的弧劣弧半圆优弧点与圆的位置关系弦(直径)等圆等弧
24.2 圆的基本性质第1课时 与圆有关的概念及点与圆的位置关系第24章 圆观察下列生活中的图片,找一找你所熟悉的图形.图片引入骑车运动看了此画,你有何想法?问题1 一些学生正在做投圈游戏,他们呈“一”字排开.这样的队形对每一人都公平吗?你认为他们应当排成什么样的队形?探究圆的概念合作探究甲丙乙丁为了使游戏公平,应在目标周围围成一个圆圈排队,因为圆上各点到圆心的距离都等于半径.为什么?·rOP◑圆的旋转定义 在平面内,线段 OP 绕着它固定的一个端点 O 旋转一周,另一个端点 P 所形成的封闭曲线叫做圆.固定的端点 O 叫做圆心,线段 OP 的长 r 叫做半径.以点 O 为圆心的圆,记作“⊙O” 读作“圆 O”.问题2 观察画圆的过程,你能说出圆是如何画出来的吗? 一是圆心,圆心确定其位置;二是半径,半径确定其大小.半径相同,圆心不同圆心相同,半径不同◑确定一个圆的要素(1) 圆上各点到定点 (圆心 O) 的距离都等于 .(2) 平面内到定点 (圆心 O) 的距离等于定长 (半径 r) 的所 有点都在 . 由此,我们可以得到圆的集合定义:平面内到定点 (圆心 O) 的距离等于定长 (半径 r) 的所有点组成的图形.Orrrrr定长(半径 r)同一个圆上想一想:从画圆的过程可以看出什么呢?·例1 如图,已知 AB,CD 为⊙O 的直径. 求证:AD∥CB. 典例精析证明:连接 AC,DB.∵ AB,CD 为⊙O 的直径,∴ OA = OB, OC = OD.∴ 四边形 ADBC 为平行四边形.∴ AD∥CB.ABCDO矩形 ABCD 的对角线 AC、BD 相交于 O.求证:A、B、C、D 在以 O 为圆心的同一圆上.证明:∵四边形 ABCD 是矩形, ∴ ∴ A、B、C、D 在以 O 为圆心,以 OA 为半径的圆上.练一练问题1 观察下图中点和圆的位置关系有哪几种?.C.... B. A..有三种:点在圆内,点在圆上,点在圆外.点和圆的位置关系观察与思考问题2 设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系下,d与r有怎样的数量关系?点P在⊙O内 点P在⊙O上 点P在⊙O外 d d drPdd Prd<r r =>r 反过来,由 d 与 r 的数量关系,怎样判定点与圆的位置关系呢?1. ⊙O 的半径为 10 cm,A、B、C 三点到圆心的距离分 别为 8 cm、10 cm、12 cm,则点 A、B、C 与⊙O 的 位置关系是点 A 在 ;点 B 在 ;点 C 在 . 圆内圆上圆外2. 圆心为 O 的两个同心圆,半径分别为 1 和 2,若 OP = ,则点 P 在 ( ) A. 大圆内 B. 小圆内 C. 小圆外 D. 大圆内,小圆外D练一练点和圆的位置关系数形结合:位置关系数量关系知识要点例2 如图,已知矩形 ABCD 的边 AB = 3,AD = 4.(1)以 A 为圆心,4 为半径作⊙A,则点 B、C、D 与 ⊙A 的位置关系如何?解:∵AB = 3 < 4, ∴ 点 B 在⊙A 内. ∵ AD = 4, ∴ 点 D 在 ⊙A 上. ∵ > 4, ∴ 点 C 在 ⊙A 外.(2)若以 A 点为圆心作⊙A, 使 B、C、D 三点中至少 有一点在圆内,且至少 有一点在圆外,求⊙A 的半径 r 的取值范围.解:由题意得,点 B 一定在圆内,点 C 一定在圆外,∴ 3<r<5.【变式题】如图,在平面直角坐标系中,点 A 的坐标为 (2,1),P 是 x 轴上一点,要使 △PAO 为等腰三角形,满足条件的 P 有几个?求出点 P 的坐标.方法总结:在没有明确腰和底边的情况下,构造等腰三角形要注意分类讨论.◑弧: 圆的有关概念◑弦: 连接圆上任意两点的线段(如图中的 AB,AC)叫做弦. 经过圆心的弦(如图中的 AB)叫做直径.注意:1. 弦和直径都是线段;2. 直径是特殊的弦,它经过圆心,是圆中最长的弦,但弦不一定是直径.◑半圆、优弧及劣弧: 圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆.劣弧与优弧 ·COAB半圆◑等圆: 能够重合的两个圆叫做等圆,等圆的半径相等.◑等弧: 在同圆或等圆中,能够互相重合的弧叫做等弧.练一练 有下列五个说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆;⑤任意一条直径都是圆的对称轴.其中错误说法的个数是 ( ) A.1 B.2 C.3 D.4解析:根据圆、直径、弦、半圆等概念来判断.半径只能确定圆的大小,不能确定圆的位置;直径是弦,但弦不一定是直径;对称轴是直线,故应说任意一条直径所在的直线是圆的对称轴.故①③⑤错误.C1. 根据圆的定义,圆指的是“圆周”,而不是“圆面”;2. 直径是圆中最长的弦.证明: 连接 OC.在△AOC 中,根据三角形三边关系有 OA + OC > AC,而 AB = 2OA,OA = OC,∴ AB > AC.知识要点例 4 如图,AB 是⊙O 的直径,CD 是⊙O 的弦,AB,CD 的延长线交于点 E. 已知 AB = 2DE,∠E = 18°,求∠AOC 的度数.解:如图,连接 OD.∵ AB 是⊙O 的直径,OC,OD 是半径,AB = 2DE,∴OD = DE.∴∠DOE = ∠E = 18°.∴∠ODC = ∠DOE+∠E = 36°.∵ OC = OD,∴∠C = ∠ODC = 36°.∴∠AOC = ∠C+∠E = 36°+18° = 54°.例 5 如图,MN 是半圆 O 的直径,正方形 ABCD 的顶点 A、D 在半圆上,B、C 在 MN 上,求证:OB = OC.ⅠⅡ10?2x在 Rt△ABO 中,AB2 + BO2 = AO2,即 (2x)2 + x2 = 102.ABOCDMN算一算:设⊙O 的半径为 10,则正方形 ABCD 的边长为 . x连接 OA,OD,则OA = OD,由三角形全等可证 OB = OC.xxxx【变式题】如图,在扇形 MON 中,∠MON = 45°,半径 MO = NO = 10,正方形 ABCD 的顶点 B、C、D 在半径 上,顶点 A 在圆弧上,求正方形 ABCD 的边长.解:连接 OA,如图.又∵∠DOC = 45°,∴CD = OC.设 AB = x,则 AB = BC = DC = OC = x.∵OA = OM = 10,∴ (2x)2 + x2 = 102.在 Rt△ABO 中,在正方形 ABCD 中,AB = BC = CD,∠ABC =∠DCB = 90°.45°1. 判断下列说法的正误,并说明理由或举反例.(1) 弦是直径;(2) 半圆是弧;(3) 过圆心的线段是直径;(4) 过圆心的直线是直径;(5) 半圆是最长的弧;(6) 直径是最长的弦;(7) 长度相等的弧是等弧.2. 填空:(1)______是圆中最长的弦,它是______的 2 倍.(2)图中有 条直径, 条非直径的弦, 圆中以 A 为一个端点的优弧有 条, 劣弧有 条.直径半径1244 3. 正方形 ABCD 的边长为 2 cm,以 A 为圆心,2 cm 长为 半径作⊙A,则点 B 在⊙A ;点 C 在⊙A ;点 D 在⊙A .上外上4. 如图,MN 为⊙O 的弦,∠MON = 70°,则∠M = °.5. 一点到⊙O 上的最近距离为 4 cm,最远距离为 10 cm, 则这个圆的半径是 .7 cm 或 3 cm55·2 cm3 cm6. 画出由所有到已知点 O 的距离大于或等于 2 cm 并且 小于或等于 3 cm 的点组成的图形.O7. 如图,OA、OB 是⊙O 的半径,点 C、D 分别为 OA、 OB 的中点,求证:AD = BC.证明:∵ OA、OB 是⊙O 的半径,∴ OA = OB.∵ 点 C、D 分别为 OA、OB 的中点,∴ OA = 2OC,OB = 2OD.∴ OC = OD.又∵∠O =∠O,∴△AOD≌△BOC (SAS).∴ BC = AD.解:渔船应沿着射线 OP 的方向航行才能尽快离开危险区.理由如下:设射线 OP 交⊙O 于点 A,过点 P 任意作一条弦 CD,连接 OD. 在△ODP中,OD-OP<PD,又∵OD = OA,∴OA-OP<PD. ∴ PA<PD,即 PA 为最短路线,故渔船沿射线 OP 方向航行才能尽快离开危险区.能力提升:8. 如图,点 O 处有一灯塔,警示⊙O 内部为危险区,一 渔船误入危险区点 P 处,该渔船应该按什么方向航行 才能尽快离开危险区?试说明理由.ADPCO圆定义旋转定义集合定义有关概念直径是圆中最长的弦弧半圆是特殊的弧劣弧半圆优弧点与圆的位置关系弦(直径)等圆等弧
相关资料
更多









