

山东省淄博市张店区2022-2023学年九年级上学期期末数学试题(含答案)
展开一、选择题(本题共10小题,每小题4分,共40分.在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项填涂在答题纸的相应位置上)
1.已知反比例函数,则它的图象不经过的点是( ).
A.B.C.D.
2.如图所示,表示两棵小树在同一时刻阳光下的影子的图形可能是( ).
A.B.C.D.
3.下列关于抛物线的说法,正确的是( ).
A.开口向下B.对称轴是直线
C.顶点坐标是D.时,y随x的增大而减小
4.在中,,若,则的度数是( ).
A.90°B.60°C.45°D.30°
5.函数与在同一坐标系内的图象可能是( ).
A.B.C.D.
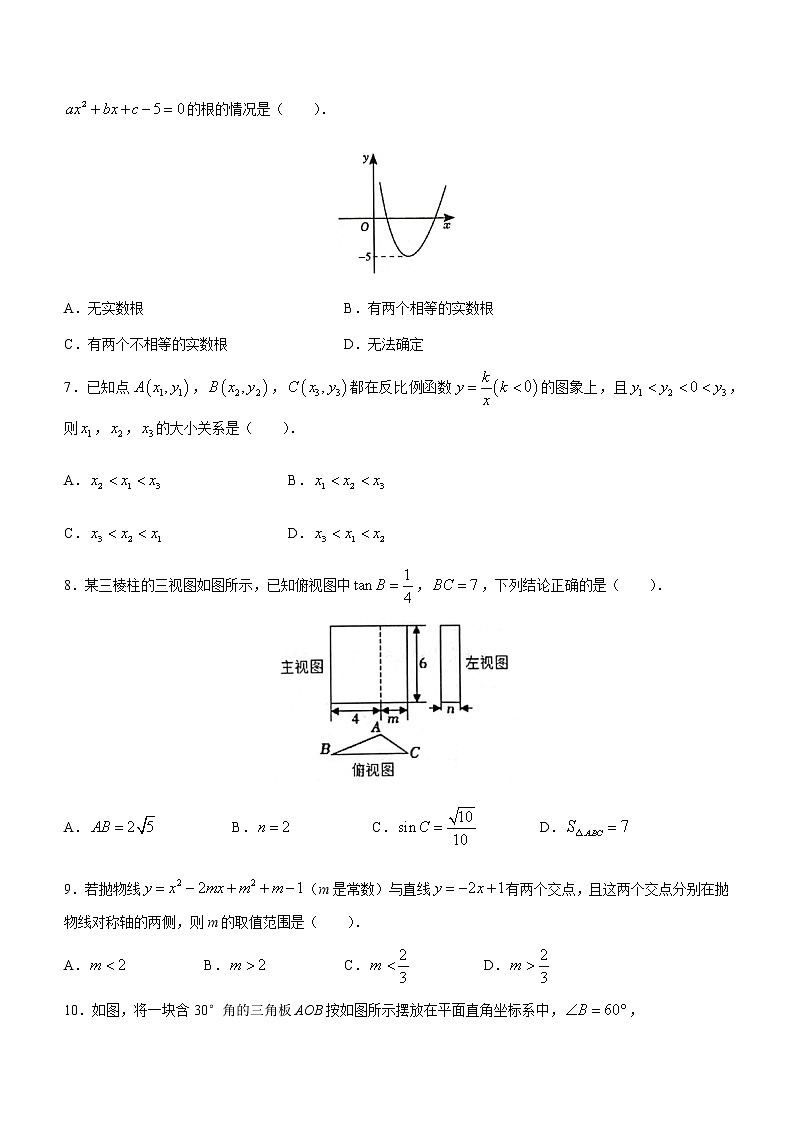
6.已知二次函数的图象如图所示,该图象顶点的纵坐标为,那么关于x的方程的根的情况是( ).
A.无实数根B.有两个相等的实数根
C.有两个不相等的实数根D.无法确定
7.已知点,,都在反比例函数的图象上,且,则,,的大小关系是( ).
A.B.
C.D.
8.某三棱柱的三视图如图所示,已知俯视图中,,下列结论正确的是( ).
A.B.C.D.
9.若抛物线(m是常数)与直线有两个交点,且这两个交点分别在抛物线对称轴的两侧,则m的取值范围是( ).
A.B.C.D.
10.如图,将一块含30°角的三角板AOB按如图所示摆放在平面直角坐标系中,,,的面积为4,BO与x轴的夹角为30°,若反比例函数的图象经过点A,则k的值为( ).
A.3B.C.6D.9
二、填空题(本大题共5小题,每小题4分,共计20分.不需写出解答过程,请把最后结果直接填写在答题卡相应位置上)
11.抛物线的顶点坐标为______.
12.反比例函数与正比例函数图象的一个交点坐标为,则另一个交点坐标为______.
13.如图所示,在边长相同的小正方形组成的网格中,两条经过格点的线段相交所成的锐角为,则夹角的正弦值为______.
14.已知二次函数的图象交直线于A,B两点.若该二次函数图象上有且只有,,三点满足,则m的值是______.
15.如图1,E是等边的边BC上一点(不与点B,C重合),连接AE,以AE为边向右作等边,连接CF.已知的面积(S)与BE的长(x)之间的函数关系如图2所示,若该抛物线顶点P的纵坐标为,则等边的面积为______.
三、解答题(本题共8小题,请把解答过程写在答题纸上)
16.计算:(1)(2)
17.如图,在中,已知,,,求AB的长.
18.如图,小明同学在晚上由路灯A走向路灯B,当他行走到P处时发现,他在路灯B下的影长PC为2米,且恰好位于路灯A的正下方,接着他又走了6.5米到Q处,此时他在路灯A下的影子恰好位于路灯B的正下方,已知小明身高1.8米,路灯B高9米.
(1)请求出路灯A与路灯B之间的距离CD的长;
(2)计算路灯A的高度.
19.某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即旅行团每增加2人,每人的单价就降低20元(每人单价不能低于580元).
(1)若某个旅行团的人数为x人,则每人的单价应为______元;
(2)请你帮助算一下,当一个旅行团的人数是多少时,旅行社可以获得最大营业额?最大营业额是多少?
20.如图1,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于点,.
(1)求反比例函数与一次函数的函数表达式;
(2)请结合图1中的图象直接写出关于x的不等式的解集;
(3)如图2,连接OB,求点A到OB的距离.
21.某种落地灯如图1所示,图2是其侧面示意图(假设台灯底座为线段GH,其高度忽略不计,灯罩和灯泡假设为点D),AB为立杆,其高为95cm;BC为支杆,它可以绕点B旋转,其中BC长为32cm;DE为悬杆,滑动悬杆可调节CD的长度,它也可以绕点C旋转.
(1)如图2所示,若将支杆BC绕点B顺时针转动使得,支杆BC与悬杆DE之间的夹角,且CD为28cm时,求点B与点D的水平距离;
(2)使用过程中发现:当灯泡与地面的距离不低于101cm且不高于105cm时,台灯光线最佳.如图3所示,现测得CD为29cm,支杆BC与悬杆DE之间的夹角,支杆BC与立杆AB之间所成的,请通过计算说明此时台灯光线是否为最佳?
(结果精确到1cm,参考数据:,,,,,,,)
22.阅读理解:
配方法是中学数学的重要方法,用配方法可求最大(小)值.对于任意正实数a,b,可作如下变形:
∵
又∵,∴
即.
根据上述内容,回答问题:若有正实数m和正实数,则当且仅当______时,这两个正实数的和有最小值为______.
思考验证:
如图1,中,,于点D,CO为AB边上中线,,,试根据图形验证成立,并指出等号成立时的条件.
探索应用:
如图2,已知C为反比例函数的图象上一点,C点的横坐标为1,点A,B为x轴上的动点(点A在点B的左边),连接AC,BC,始终保持,为y轴上一点,连接AD,BD,求四边形ADBC面积的最小值.
23.如图1,抛物线与x轴相交于点,C(点C在点B右侧),y轴相交于点,连接AB,已知面积为.
(1)求抛物线的解析式;
(2)点P是直线AC下方抛物线上一点,过点P作直线AC的垂线,垂足为点H,点P作轴交AC于点Q,求周长的最大值及此时点P的坐标;
(3)如图2,将抛物线向左平移5个单位长度得到新的抛物线,M为新抛物线对称轴上一点,N为平面内一点,使得以点A,B,M,N为顶点的四边形为菱形,请直接写出点M的坐标.
2022~2023学年度第一学期期末学业水平检测
初四数学试题答案及评分标准
一、选择题(每小题4分,共40分)
二、填空题(每小题4分,共20分)
11.12.13.14.15.
三、解答题(共8小题,共90分)
16.(本题共10分)
解:(1)
(2)
17.(本题共10分)
解:过点C作于D.
在中,∵,,,
∴,
.
在中,∵,,
∴,∴.
18.(本题共10分)
解:(1)由题意得∽,∴,
由题意知,,,
∴,解得:.
答:路灯A与路灯B之间的距离CD长10米.
(2)由题意得∽,∴,
由题意知,,
由题意知,∴,解得:米.
答:路灯A的高度为12米.
19.(本题共10分)
解:(1)
(2)设一个旅行团的人数是x人,营业额是y元,
根据题意可得:,,
∵每人单价不能低于580元,∴,
∴.
∵,
∴当时,y随x的增大而增大,
∴当一个旅行团的人数是52人时,这个旅行社可以获得最大的营业额,
最大的营业额为元.
20.(本题共12分)
解:(1)将代入得,,解得,,
所以,反比例函数表达式为:.
将代入得,,
所以,点B坐标为.
将和代入中,得,解得,
所以,一次函数表达式为:.
(2)或.
(3)设直线AB交y轴于点C,连接OA.
当一次函数中时,,
所以,C点坐标为,.
由题意得,
∵点B坐标为,∴.
设点A到OB的距离为h,则,
∴,解得,
即点A到OB的距离为.
21.(本题共12分)
解:(1)过点B作,过点C作于点Q,过点D作于点P,
由题意得:,
∵,,∴.
∵,∴,
在中,∵,∴.
在中,∵,,∴,
∵,∴,
在中,∵,
∴,
∵,
∴点B与点D的水平距离为47cm.
(2)过点B作,过点C作于点M,过点D作于点N,
由题意得:,
∵,∴,∴.
∵,∴,
在中,.
∵,∴.
∵,∴,
在中,∵,
∴.
∵,
∴灯泡与地面的距离为102.75cm.
∵,∴台灯光线是为最佳.
22.(本题共13分)
解:(1);(每空2分)
(2)∵,,∴.
在中,∵CO为中线,∴.
∵,∴.
∵,∴,∴.
又∵,,∴∽,
∴,∴.
∵,∴,即.
当D与O重合时或时,等式成立.
(3)过点C作于M.
将代入得,则点C坐标为,
∵点D坐标为,,
∴,
当AB最小时最小.
∵,,∴由(2)知:当时,AB最小,
此时,,
∴AB最小值为10,此时.
23.(本题共13分)
解:(1)∵点,∴,
∵面积为,∴,∴,
∵,∴,
∵过,,,
∴过,
∴,∴,
∴,即.
(2)∵轴,∴.
又∵,∴∽,
∴.
∵,,∴,.
∵,∴,
∴,∴,∴,
设直线AC的解析式为,
∴,解得,∴,
设,则,
∴,
∴,
∴当时,周长的最大值为,此时.
(3)∵抛物线的对称轴为直线,
∴向左平移5个单位长度得到新抛物线的对称轴为直线,
∴设.
∵,,∴.
∵,,∴由勾股定理得.
∵,∴由勾股定理得.
当AB为菱形的对角线时,,
∴,解得,
∴.
当AN为菱形的对角线时,,
∴,解得,
∴或.
当AM为菱形的对角线时,,
∴,无解,
∴不存在以AM为对角线的菱形.
综上所述:M点坐标为或或.
题号
1
2
3
4
5
6
7
8
9
10
答案
A
C
D
B
B
C
D
C
C
C
山东省淄博市张店区2023-2024学年七年级上学期1月期末数学试题: 这是一份山东省淄博市张店区2023-2024学年七年级上学期1月期末数学试题,共12页。
山东省淄博市张店区2020-2021学年九年级上学期期末数学试题: 这是一份山东省淄博市张店区2020-2021学年九年级上学期期末数学试题,共22页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
山东省淄博市张店区2023-2024学年八年级上学期1月期末数学试题: 这是一份山东省淄博市张店区2023-2024学年八年级上学期1月期末数学试题,共8页。












