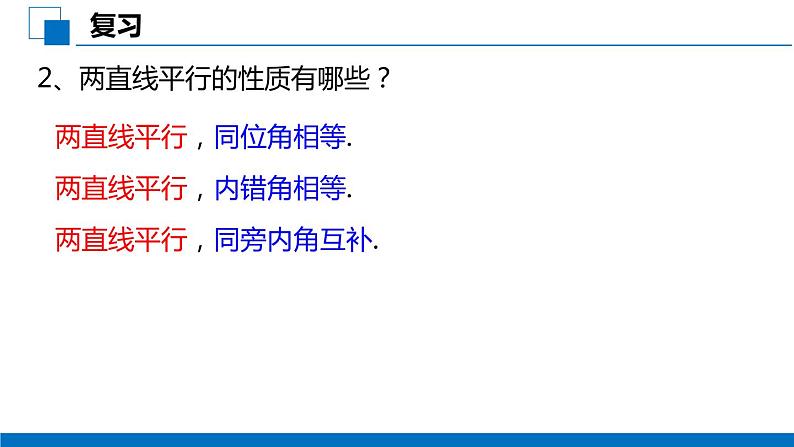
人教版七年级下册5.3.1 平行线的性质优秀课件ppt

这是一份人教版七年级下册5.3.1 平行线的性质优秀课件ppt，共18页。PPT课件主要包含了角的数量关系，证明AD∥EF，角之间的关系，∵AB∥CD，∴∠ABC∠BCD，∵∠1∠2，即∠3∠4，∴BE∥CF，∴EF∥CD，过点E作EF∥AB等内容，欢迎下载使用。
1、判定两直线平行的方法有哪些？
同旁内角互补，两直线平行.
内错角相等，两直线平行.
同位角相等，两直线平行.
垂直于同一直线的两直线平行.
平行于同一直线的两直线平行.
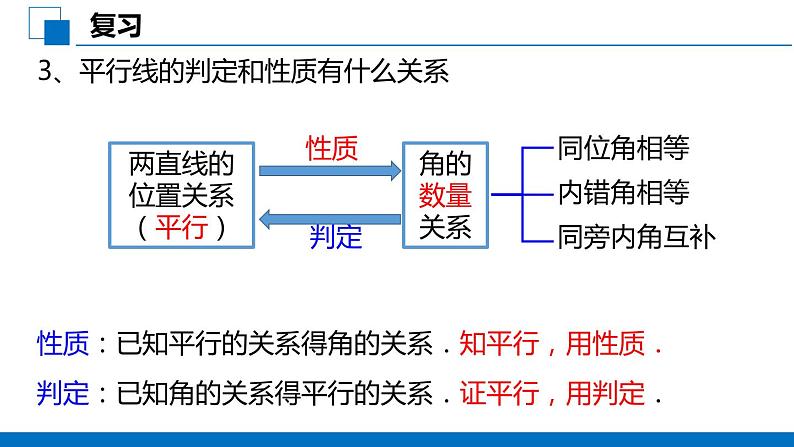
两直线平行，同旁内角互补.
两直线平行，内错角相等.
两直线平行，同位角相等.
2、两直线平行的性质有哪些？
3、平行线的判定和性质有什么关系
两直线的位置关系（平行）
判定：已知角的关系得平行的关系．证平行，用判定．
性质：已知平行的关系得角的关系．知平行，用性质．
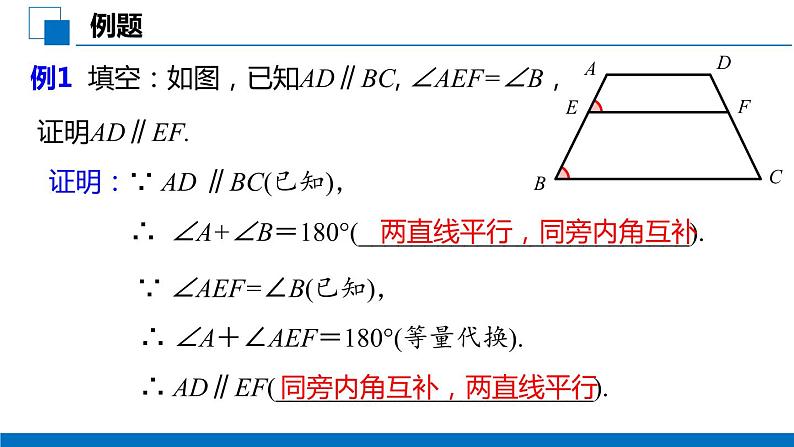
例1 填空：如图，已知AD∥BC, ∠AEF=∠B，
∴ ∠A+∠B＝180°(_________________________).
两直线平行，同旁内角互补
同旁内角互补，两直线平行
证明：∵ AD ∥BC(已知)，
∵ ∠AEF=∠B(已知)，
∴ ∠A＋∠AEF＝180°(等量代换).
∴ AD∥EF(________________________).
1、如图，AB∥EF，∠ECD=∠E，则∠A=∠ECD.理由如下：
∵∠ECD=∠E∴CD∥EF(________________________)∵AB∥EF∴CD∥AB( _________________________________).∴∠A=∠ECD(_______________________).
内错角相等，两直线平行
平行于同一直线的两条直线互相平行
两直线平行,同位角相等
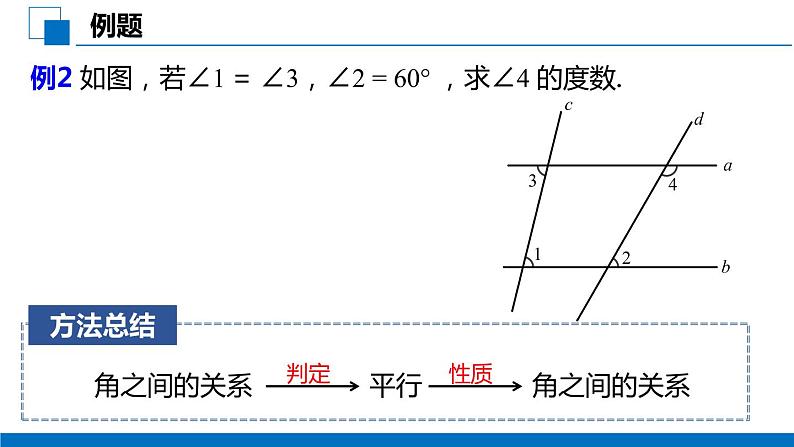
例2 如图，若∠1 = ∠3，∠2 = 60° ，求∠4 的度数.
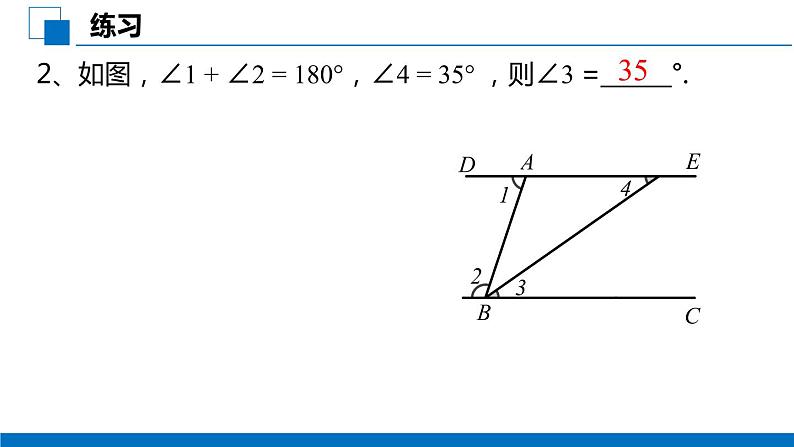
2、如图，∠1 + ∠2 = 180°，∠4 = 35° ，则∠3 =______°.
3、如图，DA⊥AB，CD⊥DA，∠B = 56° ，则∠C =______°.
例3 如图，AB∥CD，∠1 = ∠2.请说明：BE∥CF.
（两直线平行，内错角相等）
∴∠ABC -∠1=∠BCD -∠2
（内错角相等，两直线平行）
4、如图，∠1 = ∠2，∠E = ∠F ，那么 AB∥CD 吗？为什么？
在已知图形中添些线(线段或圆)以构造用于证明或计算中的基本图形,所添的线叫辅助线。
例4 如图，AB∥CD，你能确定∠B、∠D与∠BED 的大小关系吗？说说你的看法．
即∠B＋∠D＝∠DEB．
∵AB∥CD，EF∥AB
∴∠B＋∠D＝∠BEF＋∠DEF＝∠DEB
如图，若AB∥CD，则
∠B＋∠F＋∠D＝∠E ＋∠G
∠B＋∠F1＋…＋∠Fn-1＋∠D＝∠E1＋…＋∠En-1＋∠En
如图，AB∥CD，你能确定∠B、∠D与∠BED 的大小关系吗？说说你的看法．
即∠B＋∠D＋∠DEB＝360°．
∴∠B＋∠BEF＝180°
∴∠D ＋∠DEF＝180°
∴∠B＋∠D＋∠BED＝∠B＋∠BEF＋ ∠DEF＋∠D＝360°
∠B＋∠D＋∠E＝360°
∠B＋∠D＋∠E＋∠F＝540°
∠B＋∠D＋∠E ＋∠F＋∠G＝720°
∠B＋∠E1＋∠E2＋…＋∠En＋∠D＝180°(n-1)