高中数学人教A版 (2019)必修 第一册1.5 全称量词与存在量词课前预习ppt课件

这是一份高中数学人教A版 (2019)必修 第一册1.5 全称量词与存在量词课前预习ppt课件，共32页。PPT课件主要包含了目标认知，全称量词命题，∀x∈Mpx，存在量词命题，∃x∈Mpx，a≥12等内容，欢迎下载使用。

任意号(全称量词)“∀”来源于英语中的Arbitrary一词,因为小写和大写均容易造成混淆,故将其单词首字母大写后倒置.同样,存在号(存在量词)“∃”来源于Exist一词中E的反写.存在(∃)是只要一个集合中有一个元素满足就行,任意(∀)是一个集合中任意一个元素都满足.
1.短语“所有的”“任意一个”在逻辑中通常叫作全称量词,并用符号“　　　”表示,含有全称量词的命题叫作　　　　　　　　. 2.将含有变量x的语句用p(x),q(x),r(x),… 表示,变量x的取值范围用M表示.那么,全称量词命题“对M中任意一个x,p(x)成立”可用符号简记为　　　　　　. 
知识点一　全称量词与全称量词命题
【诊断分析】 判断正误.(请在括号中打“√”或“×”)(1)“对每一个无理数x,x2也是无理数”是全称量词命题,也是真命题.(　　)(2)“有的质数是奇数”是全称量词命题.(　　)
[解析] “所有质数都是奇数”才是全称量词命题.(2)错误.
(3)“三角形的内角和等于180°”是全称量词命题.(　　)(4)“∀x∈R,x2+1≥1”是真命题.(　　)
[解析] “三角形的内角和等于180°”即“所有的三角形的内角和都等于180°”,是全称量词命题.
[解析]对任意x∈R,x2≥0恒成立,则x2+1≥1,因此“∀x∈R,x2+1≥1”是真命题.
知识点二　存在量词与存在量词命题
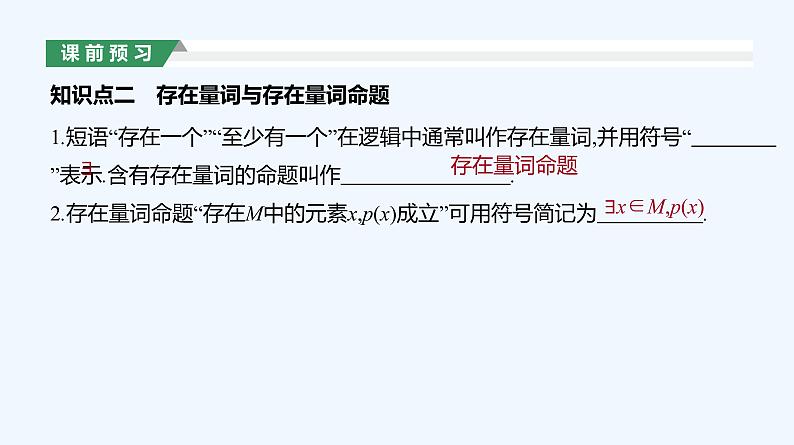
1.短语“存在一个”“至少有一个”在逻辑中通常叫作存在量词,并用符号“　　　　”表示.含有存在量词的命题叫作　　　　　　　　. 2.存在量词命题“存在M中的元素x,p(x)成立”可用符号简记为　　　　　. 
【诊断分析】 判断正误.(请在括号中打“√”或“×”)(1)“至少有一个三角形没有外接圆”是存在量词命题.(　　)(2)“在一个平面内,存在两条相交直线垂直于同一条直线”不是存在量词命题. (　　)
[解析] “至少有一个三角形没有外接圆”有存在量词,所以是存在量词命题.
[解析] “在一个平面内,存在两条相交直线垂直于同一条直线”有存在量词,所以是存在量词命题.
(3)“有些三角形的三个内角相等”是存在量词命题.(　　)(4)“至少有一个偶数是质数”是存在量词命题且是真命题.(　　)
[解析] “有些三角形的三个内角相等”有存在量词,所以是存在量词命题.
[解析]因为偶数2是质数,所以“至少有一个偶数是质数”是存在量词命题且是真命题.
1.全称量词与存在量词(1)全称量词是命题中常见的量词,理解此类命题的关键是对量词的把握.(2)存在性问题是数学中的一类重要问题,存在量词是描述这一类问题的关键词语.
2.关于全称量词命题和存在量词命题的理解(1)全称量词命题强调命题的一般性,是对于某一个给定集合的所有元素是否具有某种性质来说的.(2)存在量词命题强调命题的存在性,是对于某一个给定集合的某些元素是否具有某种性质来说的.(3)全称量词命题和存在量词命题是具有相对性的,即满足某种性质的元素所对应的集合不同,可能导致命题的性质不同.
3.对于两种命题符号表达的理解(1)体现变量x代表的是某给定集合M的所有元素还是指定元素.(2)指出变量x所满足的性质p(x).
例1 判断下列命题是全称量词命题还是存在量词命题.(1)凸多边形的外角和等于360°;(2)有的速度方向不定;(3)圆周上任意一点到圆心的距离都等于圆的半径;(4)有些一次函数的图像经过原点.
探究点一　全称量词命题和存在量词命题的判断
解:(1)命题的完整表述应为“所有凸多边形的外角和都等于360°”,故为全称量词命题.(2) 含有存在量词“有的”,故是存在量词命题.(3)含有全称量词“任意”,故是全称量词命题.(4) 含有存在量词“有些”,故是存在量词命题.
变式 判断下列命题是全称量词命题还是存在量词命题,并用符号“∀”或“∃”表述出来.(1)任意一个实数乘-1都等于它的相反数;(2)存在实数x,使x2+2x+8=0成立;(3)实数的平方大于或等于零;(4)有的三角形至少有两个锐角.
解:(1)全称量词命题,∀x∈R,x·(-1)=-x.(2)存在量词命题,∃x∈R,x2+2x+8=0.(3)全称量词命题,∀x∈R,x2≥0.(4)存在量词命题,∃x∈{x|x是三角形},x至少有两个锐角.
[素养小结](1)判断一个语句是全称量词命题还是存在量词命题的步骤:
(2)全称量词命题和存在量词命题的不同表述方法:
探究点二　全称量词命题和存在量词命题的真假判断
变式 下列命题中是全称量词命题,也是真命题的是(　　)A.所有菱形的四条边都相等B.∃x∈N,2x为偶数C.∀x∈R,x2+2x+1>0D.π是无理数
[解析] 对于A,所有菱形的四条边都相等,是全称量词命题,也是真命题.对于B,∃x∈N,2x为偶数,是存在量词命题.对于C,∀x∈R,x2+2x+1>0,是全称量词命题,但它是假命题.对于D,π是无理数,不是全称量词命题.故选A.
[素养小结](1)全称量词命题的真假判断:(2)存在量词命题的真假判断:
探究点三　利用全称量词命题与存在量词命题求参数的范围
例3 (1)已知p:∃x∈R,x2+4x+a=0,若p是真命题,则实数a的取值范围是(　　)A.0[解析]因为p是真命题,所以方程x2+4x+a=0有实数根,即Δ=16-4a≥0,即a≤4.故选B.
(2)[2021·湖北沙市中学高一月考] 若命题“∀x∈{x|0<2x-3<5},一次函数y=3x-a的图像都在x轴的下方”为真命题,则实数a的取值范围是　　　　. 
变式 若“∀x∈R,x2-2ax+2≥a-a2”是真命题,求实数a的取值范围.
解:因为“∀x∈R,x2-2ax+2≥a-a2”是真命题,所以a-a2小于或等于y=x2-2ax+2的最小值,因为y=x2-2ax+2=(x-a)2+2-a2,所以当x=a时,y=x2-2ax+2取得最小值2-a2,所以2-a2≥a-a2,得a≤2.
[素养小结]根据含量词命题的真假等价转化为关于参数的不等式(组),解不等式(组)求参数范围.
1.理解全称量词命题及存在量词命题时应注意的问题(1)全称量词命题就是陈述某集合中所有元素都具有某种性质的命题,常见的全称量词还有“一切”“每一个”等,相应的词语是“都”.(2)有些命题省去了全称量词,但仍是全称量词命题,如“有理数是实数”,就是“所有的有理数都是实数”.(3)存在量词命题就是陈述某集合中存在一个或部分元素具有某种性质的命题,常见的存在量词还有“有的”“存在”等.
例 判断下列命题是全称量词命题还是存在量词命题.(1)至少有一个三角形没有外接圆;(2)任意一个有理数都能写成分数形式.
解:(1)是存在量词命题,“至少有一个”为存在量词.(2)是全称量词命题,“任意一个”是全称量词.
2.根据全称量词命题、存在量词命题求参数的范围存在量词命题是真命题,可以转化为能成立问题解决;全称量词命题是真命题,可以转化为恒成立问题解决.
1.给出下列命题:①任意一个自然数都是正整数;②有的平行四边形也是菱形;③三角形的内角和是180°.其中全称量词命题的个数是(　　)A.0 B.1 C.2 D.3
[解析] ①③是全称量词命题.
2.下列命题中,是存在量词命题的是(　　)A.任何一个实数乘0都等于0B.自然数都是正整数C.存在一个数既是偶数又是负数D.过平面内两点有且只有一条直线
[解析] “存在一个数既是偶数又是负数”是存在量词命题.
3.下列存在量词命题是假命题的是(　　)A.存在一个四边形有外接圆B.存在x∈R,使x2+x+1=0成立C.有的素数是奇数D.有的有理数没有倒数
4.命题“∃x∈R,x2+2x+5=0”是　　　　　　　(填“全称量词命题”或“存在量词命题”),它是　　　　命题(填“真”或“假”).