



高中人教A版 (2019)第二章 一元二次函数、方程和不等式2.2 基本不等式教课ppt课件
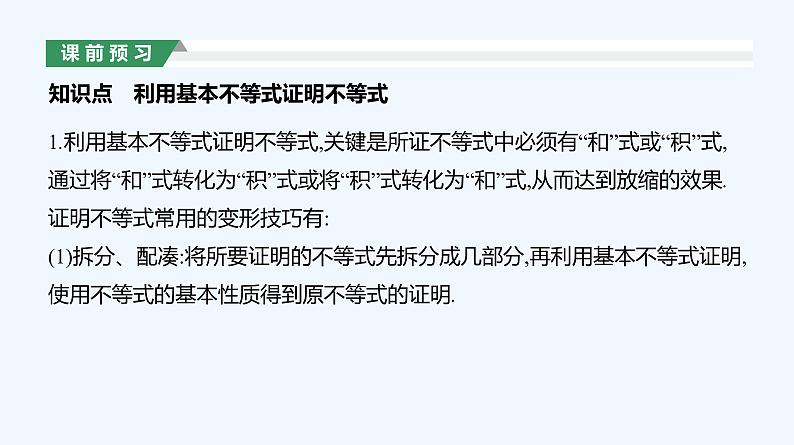
展开1.利用基本不等式证明不等式,关键是所证不等式中必须有“和”式或“积”式,通过将“和”式转化为“积”式或将“积”式转化为“和”式,从而达到放缩的效果.证明不等式常用的变形技巧有:(1)拆分、配凑:将所要证明的不等式先拆分成几部分,再利用基本不等式证明,使用不等式的基本性质得到原不等式的证明.
知识点 利用基本不等式证明不等式
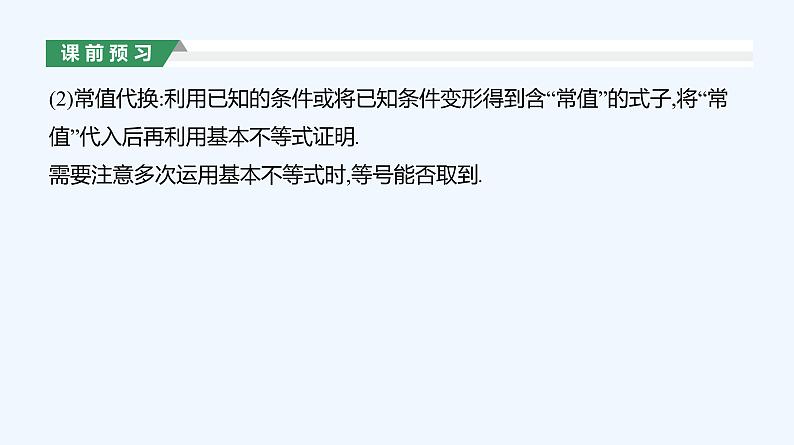
(2)常值代换:利用已知的条件或将已知条件变形得到含“常值”的式子,将“常值”代入后再利用基本不等式证明.需要注意多次运用基本不等式时,等号能否取到.
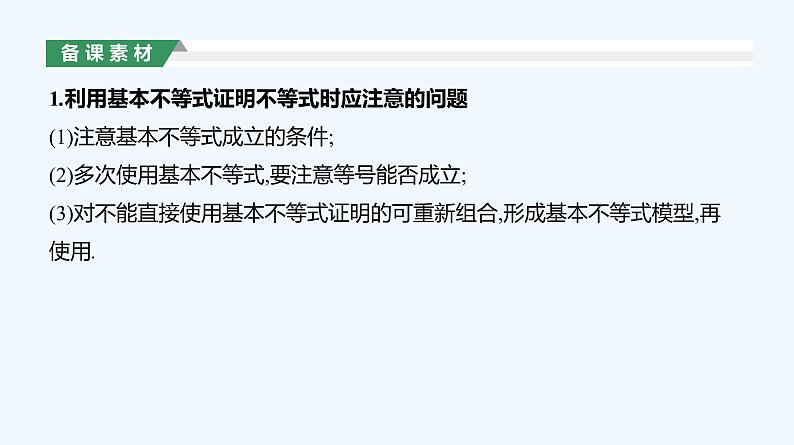
1.利用基本不等式证明不等式时应注意的问题(1)注意基本不等式成立的条件;(2)多次使用基本不等式,要注意等号能否成立;(3)对不能直接使用基本不等式证明的可重新组合,形成基本不等式模型,再使用.
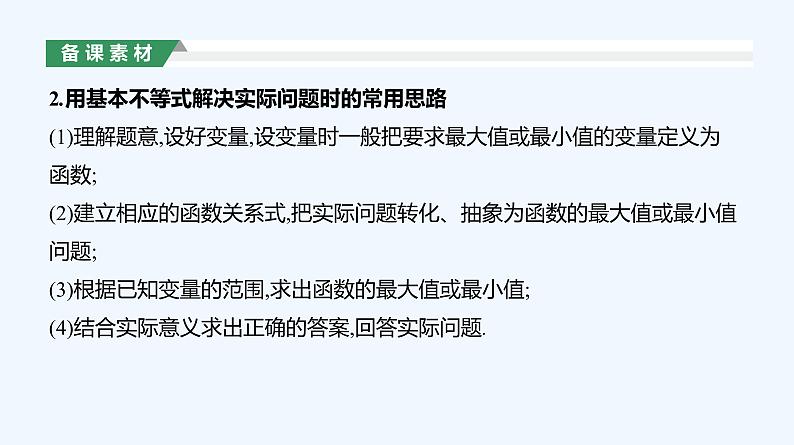
2.用基本不等式解决实际问题时的常用思路(1)理解题意,设好变量,设变量时一般把要求最大值或最小值的变量定义为函数;(2)建立相应的函数关系式,把实际问题转化、抽象为函数的最大值或最小值问题;(3)根据已知变量的范围,求出函数的最大值或最小值;(4)结合实际意义求出正确的答案,回答实际问题.
探究点一 利用基本不等式求参数
[素养小结]利用基本不等式求参数问题,大部分为不等式恒成立问题,解决时,一般转化为利用基本不等式求最值问题或使用基本不等式时等号成立的条件问题.特别要注意应用基本不等式的条件与变形技巧.
例2 (1)设a,b,c∈R,求证:a2+b2+c2≥ab+bc+ca.
探究点二 利用基本不等式证明不等式
证明:∵a2+b2≥2ab(当且仅当a=b时取等号),b2+c2≥2bc(当且仅当b=c时取等号),c2+a2≥2ca(当且仅当a=c时取等号),∴(a2+b2)+(b2+c2)+(c2+a2)≥2ab+2bc+2ca(当且仅当a=b=c时等号成立),∴a2+b2+c2≥ab+bc+ca.
[素养小结]利用基本不等式证明不等式时,要先观察题中要证明的不等式的结构特征,若不能直接使用基本不等式证明,则考虑对代数式进行拆项、变形、配凑等,使之达到能使用基本不等式的形式;若题目中还有已知条件,则先观察已知条件和所证不等式之间的联系,当已知条件中含有“1”时,要注意“1”的代换.另外,解题时要时刻注意等号能否取到.
例3 [2021·安徽蚌埠二中高一月考] 如图2-2-1,在半径为40 cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中A,B在直径上,点C,D在圆周上.设AD=x cm,矩形ABCD的面积为y cm2.(1)写出y与x的关系式,并写出x的取值范围.
探究点三 基本不等式在实际问题中的应用
例3 [2021·安徽蚌埠二中高一月考] 如图2-2-1,在半径为40 cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中A,B在直径上,点C,D在圆周上.设AD=x cm,矩形ABCD的面积为y cm2.(2)怎样截取才能使矩形材料ABCD的面积最大?并求出最大面积.
[素养小结]利用基本不等式解决实际问题时,首先审清题意,然后将实际问题转化为数学问题,再利用数学知识解决问题.
1.基本不等式链的几何证明
2.解决实际应用问题,关键在于弄清问题的各种数量关系,抽象出数学模型,利用基本不等式解应用题,既要注意条件是否具备,还要注意有关量的实际含义.
例2 如图,某居民小区要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的面积为200平方米的十字形.计划在正方形MNPQ上建一座花坛,造价为4200元/平方米,在四个相同的矩形(图中阴影部分)上铺花岗岩地坪,造价为210元/平方米,在四个空角(图中四个三角形)上铺草坪,造价为80元/平方米.(1)设总造价为S元,AD的长为x米,求S与x的关系式.(2)当AD的长为多少时,总造价最低?并求最低总造价.
高中数学人教A版 (2019)必修 第一册2.2 基本不等式评课课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册2.2 基本不等式评课课件ppt,共10页。PPT课件主要包含了若a0b0则,通常我们把上式写作,适用范围,a0b0,新课引入,典型例题,变式练习,则篱笆的长为,即x12y6,x+2y24等内容,欢迎下载使用。
人教A版 (2019)必修 第一册2.2 基本不等式教课内容课件ppt: 这是一份人教A版 (2019)必修 第一册2.2 基本不等式教课内容课件ppt,共38页。PPT课件主要包含了目标认知,两个重要不等式,知识点一基本不等式,不小于,知识点二最值定理,①②③等内容,欢迎下载使用。
人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.2 基本不等式背景图课件ppt: 这是一份人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.2 基本不等式背景图课件ppt,共17页。PPT课件主要包含了一正二定三相等,知识回顾,a=b,x=y,典例1,归纳总结等内容,欢迎下载使用。













