






- 4.4.3 不同函数增长的差异课件PPT 课件 0 次下载
- 4.5.1 函数的零点与方程的解课件PPT 课件 0 次下载
- 4.5.3 函数模型的应用课件PPT 课件 0 次下载
- 5.1.1 任意角课件PPT 课件 0 次下载
- 5.1.2 弧度制课件PPT 课件 0 次下载
高中数学4.5 函数的应用(二)课文课件ppt
展开对于在区间[a,b]上图像连续不断且 的函数y=f(x),通过不断地把它的零点所在区间 ,使所得区间的两个端点 ,进而得到零点 的方法叫作二分法.
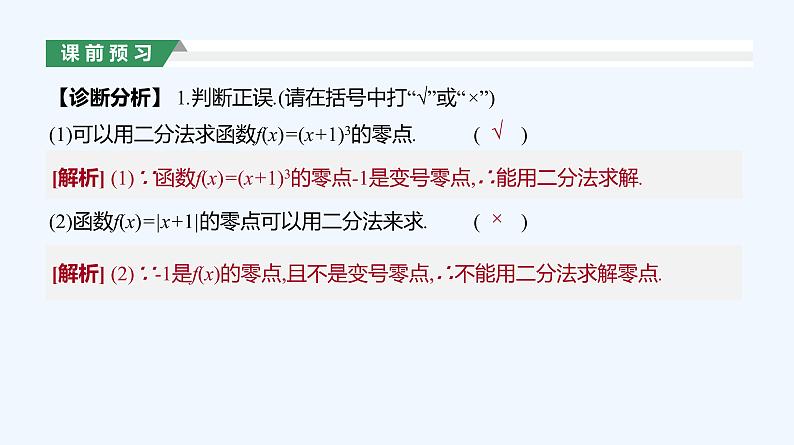
【诊断分析】 1.判断正误.(请在括号中打“√”或“×”)(1)可以用二分法求函数f(x)=(x+1)3的零点.( )(2)函数f(x)=|x+1|的零点可以用二分法来求.( )
[解析] (1)∵函数f(x)=(x+1)3的零点-1是变号零点,∴能用二分法求解.
[解析] (2)∵-1是f(x)的零点,且不是变号零点,∴不能用二分法求解零点.
2.用二分法求函数零点的适用条件是什么?
解:①f(x)的图像在区间[a,b]上连续不断;②f(a)f(b)<0.
知识点二 用二分法求方程近似解的步骤
(3)计算f(c),并进一步确定零点所在的区间.①若 (此时x0=c),则c就是函数的零点;②若f(a)·f(c)<0(此时x0∈ ),则令b=c;③若f(c)·f(b)<0(此时x0∈(c,b)),则令a=c.这一步的目的在于缩小零点所在的区间,也就是所谓的“二分”. (4)判断是否达到精确度ε:若 ,则得到零点近似值a(或b);否则重复第(2)(3)(4)步.
【诊断分析】 1.判断正误.(请在括号中打“√”或“×”)(1)用二分法求函数零点的近似值时,每次等分区间后,零点必定在左侧区间内.( )(2)用二分法所求出的方程的解都是近似解.( )
[解析] (1)用二分法求函数零点的近似值时,每次等分区间后,零点既可以在左侧区间内,也可以在右侧区间内.
[解析] (2)用二分法所求出的方程的解不一定是近似解.
(3)精确度ε就是近似值.( )(4)用二分法求方程f(x)=0在区间[0,1]上的近似解时,经计算,f(0.5)<0,f(0.562 5)<0,f(0.625)>0,即得到方程的一个近似解可以为0.625(精确度为0.1).( )
[解析] (3)精确度ε是对方程近似解的精确度要求.
[解析] (4)因为|0.625-0.562 5|=0.062 5<0.1,所以0.562 5或0.625都可以作为方程f(x)=0的一个近似解.
2.(1)用二分法求方程的近似解时,如何决定步骤的结束?(2)你知道为什么当|a-b|<ε时,可将a或b的值看成方程的近似解吗?
解:(1)根据精确度的大小,当零点所在的区间的两个端点值差的绝对值小于精确度ε时,步骤结束.
解:(2)当|a-b|<ε时,由于方程根的真实值x0∈(a,b),所以|a-x0|<|a-b|<ε,所以a与方程根的真实值x0的误差不超过精确度ε,故可以用a来作为方程的近似解.同理,b也可以用来作为方程的近似解.
应用二分法求方程的近似解应注意的问题(1)题目对根的要求有两类,注意区分:一是“精确度”,如果区间(a,b)满足|a-b|<ε,则称达到精确度ε的近似解为a(或b);二是“精确到ε”,这要求通过二分法得到的区间端点的精确值为ε.(2)二分法不是万能的,只有满足①y=f(x)的图像在区间(a,b)上是连续的,②f(a)·f(b)<0,此时方程f(x)=0才能求解.因此,它只能求解函数的变号零点,不能求解不变号零点.
探究点一 二分法的概念
例1 (1)(多选题)下列图像对应的函数中能用二分法求零点的是( ) AB CD图4-5-2
[解析] (1)观察图像与x轴的交点,若交点附近的函数图像连续,且交点两侧的函数值符号相异,则可用二分法求零点,故选ACD.
(2)已知函数f(x)=x3-2x-5,用二分法求f(x)在区间(2,3)内的零点时,取区间的中点为2.5,那么零点所在的下一个区间是 .
[解析] (2)因为f(2)=23-2×2-5=-1<0,f(2.5)=2.53-2×2.5-5=5.625>0,f(3)=33-2×3-5=16>0,所以f(2)f(2.5)<0,所以零点所在的下一个区间是(2,2.5).
变式 (1)已知函数f(x)的图像如图4-5-3所示,其中零点的个数与可以用二分法求解的零点的个数分别为( ) 图4-5-3A.4,4 B.3,4C.5,4 D.4,3
[解析] (1)函数图像与x轴有4个交点,所以零点的个数为4.左右函数值异号的零点有3个,所以可以用二分法求解的零点的个数为3.故选D.
(2)如图4-5-4所示,下列函数的图像与x轴均有交点,其中不能用二分法求零点的是( ) A B C D图4-5-4
[解析] (2)根据二分法的定义,只有f(x)在[a,b]上是连续的,且f(a)·f(b)<0,才能不断地把函数零点所在的区间一分为二,进而求出函数的零点.结合各图像可得选项B,C,D满足条件,而选项A不满足.在A中,图像经过零点x0时,函数值不变号,因此不能用二分法求解.故选A.
[素养小结]判断一个函数能否用二分法求其零点的依据是其图像在零点附近是连续不断的,且该零点为变号零点.因此,用二分法求函数的零点近似值的方法仅对函数的变号零点适用,对函数的不变号零点不适用.
探究点二 求方程的近似解
[探索] 利用二分法可以求方程的近似解,那么怎样求方程x2-2=0的正的近似解?
解:令f(x)=x2-2,找出零点所在的初始区间[1,2],然后根据二分法求出在一定精确度下的方程的近似解.
例2 (1)用二分法求函数f(x)=x3+3x-1的零点时,第一次计算f(0)<0,f(0.5)>0,可得其零点x0∈ ,第二次应计算 .以上横线上应填的内容为( ) A.(0,0.5),f(0.25)B.(0,1),f(0.25)C.(0.5,1),f(0.75) D.(0,0.5),f(0.125)
[解析] (1)由f(0)<0,f(0.5)>0,知x0∈(0,0.5),再计算(0,0.5)的中点0.25对应的函数值f(0.25),以判断x0的准确位置.
(2)[2021·陕西咸阳高新一中高一期中] 若函数f(x)=x3+x2-2x-2的一个正零点附近的函数值如下表所示.如果精确度为0.05,那么方程x3+x2-2x-2=0的一个近似解为( ) 5 D.1.5
[解析] (2)因为|1.375-1.437 5|=0.062 5>0.05,|1.437 5-1.406 25|=0.031 25<0.05,所以方程x3+x2-2x-2=0的近似解为1.437 5或1.406 25.故选C.
变式 用二分法求2x+x=4在[1,2]内的近似解(精确度为0.2).参考数据:
解:令f(x)=2x+x-4,则f(x)在R上是增函数,f(1)=2+1-4<0,f(2)=22+2-4>0,经计算可得下表,∵|1.375-1.5|=0.125<0.2,∴2x+x=4在[1,2]内的近似解可以为1.375.
[素养小结]用二分法求方程的近似解的思路和方法:(1)根据函数的零点与相应方程解的关系,求函数的零点与求相应方程的解是等价的,所以求方程f(x)=0的近似解,可按照用二分法求函数零点近似值的步骤求解.(2)对于求形如f(x)=g(x)的方程的近似解,可以通过移项化为求函数F(x)=f(x)-g(x)的零点的近似值,然后按照用二分法求函数零点近似值的步骤求解.
求函数零点的近似值利用二分法求函数y=f(x)在区间(a,b)上的零点,就是不断地把函数y=f(x)的零点所在的区间一分为二,并通过判断区间两端点处函数值乘积的正负情况,使区间的两个端点逐步逼近零点,从而找到零点的近似值.
因为|0.273 437 5-0.281 25|=0.007 812 5<0.01,所以方程的根的近似值为0.273 437 5,即f(x)=0的正根约为0.273 437 5.
1.下列关于二分法求函数的零点的近似值的说法中正确的是( )A.适用于在零点处连续且零点两侧函数值异号的函数B.适用于在零点处连续且零点两侧函数值同号的函数C.适用于所有函数D.所有函数都不适用
[解析] 由函数零点存在定理可知选A.
2.用二分法求方程x3+2x-9=0的近似解中,已知f(x)=x3+2x-9的部分函数值或函数值的近似值如下表所示:则当精确度为0.1时,方程x3+2x-9=0的近似解可以为( )D.1.9
[解析] f(x)在R上是增函数,根据表中数据可知f(1.75)=-0.14<0,f(1.812 5)=0.579 3>0,且|1.75-1.812 5|=0.062 5<0.1,结合选项,所以方程的近似解可以为1.75.
5.[2021·浙江宁波高一期末] 给出以下数据:在精确度为0.05的要求下,方程3x=x+4的一个近似解可以为 .(填序号) ①-1;②1.5;③1.562 5;④1.75.
高中数学人教A版 (2019)必修 第一册4.5 函数的应用(二)授课课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册4.5 函数的应用(二)授课课件ppt,共27页。PPT课件主要包含了新课导入,引入问题探讨方法,函数零点存在定理,函数单调性,函数零点个数,方程实数解的个数,解决问题实施方法,总结提炼归纳方法,归纳出二分法的定义,确定初始区间等内容,欢迎下载使用。
高中人教A版 (2019)第四章 指数函数与对数函数4.5 函数的应用(二)多媒体教学课件ppt: 这是一份高中人教A版 (2019)第四章 指数函数与对数函数4.5 函数的应用(二)多媒体教学课件ppt,共34页。
人教A版 (2019)必修 第一册4.5 函数的应用(二)课文配套课件ppt: 这是一份人教A版 (2019)必修 第一册4.5 函数的应用(二)课文配套课件ppt,共20页。PPT课件主要包含了零点存在性定理,问题1,算一算,方法分析,资料查询,-0009,-0084,二分法定义,二分法步骤,计算fc等内容,欢迎下载使用。













