高中数学人教A版 (2019)必修 第一册4.5 函数的应用（二）多媒体教学ppt课件

这是一份高中数学人教A版 (2019)必修 第一册4.5 函数的应用（二）多媒体教学ppt课件，共47页。PPT课件主要包含了目标认知，图4-5-5，图4-5-6等内容，欢迎下载使用。
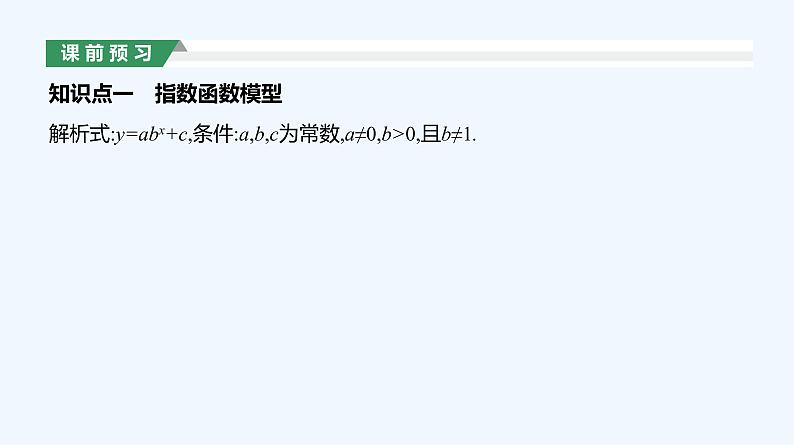
知识点一　指数函数模型
解析式:y=abx+c,条件:a,b,c为常数,a≠0,b>0,且b≠1.
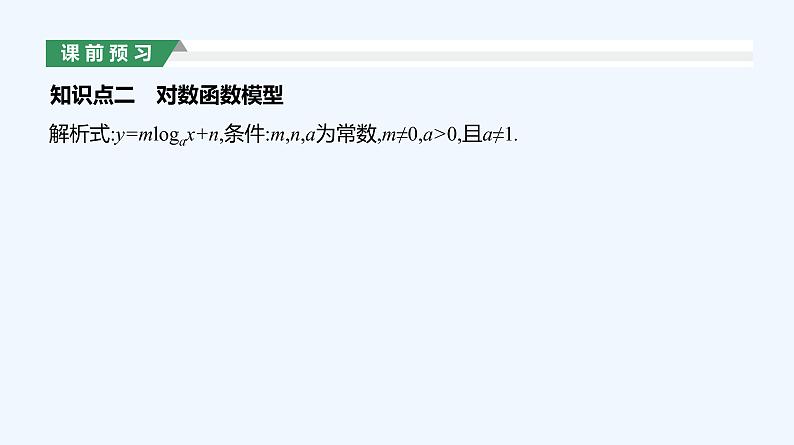
知识点二　对数函数模型
解析式:y=mlgax+n,条件:m,n,a为常数,m≠0,a>0,且a≠1.
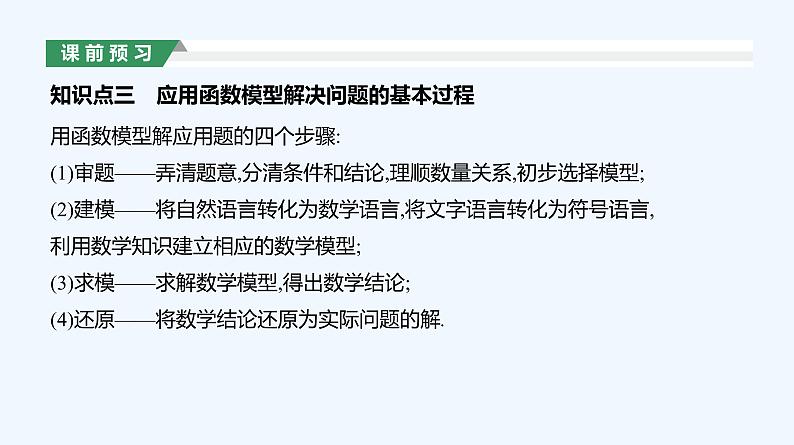
知识点三　应用函数模型解决问题的基本过程
用函数模型解应用题的四个步骤:(1)审题——弄清题意,分清条件和结论,理顺数量关系,初步选择模型;(2)建模——将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识建立相应的数学模型;(3)求模——求解数学模型,得出数学结论;(4)还原——将数学结论还原为实际问题的解.
1.何为数学建模?其目的是什么?对现实生活中的实际问题加以提炼,抽象为数学模型,求出模型的解,验证模的可靠性与合理性,并用该数学模型的信息来解决现实问题.数学知识的这一应用过程称为数学建模,所以数学建模的目的就是用数学知识解决实际问题.
2.建立函数模型应把握三关(1)事理关:通过阅读、理解,明白问题讲什么,熟悉实际背景,为解题打开突破口.(2)文理关:将实际问题的文字语言转化为数学的符号语言,用数学式子表达数量关系.(3)数理关:在构建数学模型的过程中,对已有的数学知识进行检验,从而认定或构建相应的数学问题.
探究点一　指数函数模型
例1 [2021·安徽安庆高一月考] 国家正在大力倡导环保意识、生态意识,构建全社会共同参与的环境治理体系,让生态环保思想成为社会生活中的主流文化.某化工企业通过改良工艺,使排放的废气中含有的污染物数量逐渐减少.已知改良工艺前所排放的废气中含有的污染物数量r0=2 mg/m3,首次改良工艺后排放的废气中含有污染物数量r1=1.94 mg/m3,第n次改良后所排放的废气中的污染物数量rn可由函数模型rn=r0-(r0-r1)·50.5n+p(p∈R,n∈N*)给出,其中n是指改良工艺的次数.(1)试求改良后所排放的废气中含有的污染物数量的函数模型. (2)依据国家环保要求,企业所排放的废气中含有的污染物数量不能超过0.08 mg/m3.试问:至少改良多少次工艺后才能使该企业所排放的废气中含有污染物数量达标?(参考数据:lg 2≈0.3)
解:(1)由题意得r0=2,r1=1.94,所以当n=1时,r1=r0-(r0-r1)·50.5+p,即1.94=2-(2-1.94)×50.5+p,解得p=-0.5,所以rn=2-0.06×50.5n-0.5(n∈N*),故改良后所排放的废气中含有的污染物数量的函数模型为rn=2-0.06×50.5n-0.5(n∈N*).
变式 [2021·安徽阜阳高一月考] 医学上为研究传染病传播时病毒细胞的发展规律及其预防,将病毒细胞注入一只小白鼠体内进行实验.检测后,将病毒细胞的总数与天数的关系记录如下表所示.已知该种病毒细胞在小白鼠体内的个数超过108的时候小白鼠将死亡,但注射某种药物,可杀死小白鼠体内98%的病毒细胞.(1)为了使小白鼠在实验过程中不死亡,第一次最迟应在何时注射该种药物?(精确到天)(2)第二次最迟应在何时注射该种药物,才能维持小白鼠的生命?(精确到天)(参考数据:lg 2≈0.301 0)
[素养小结]在解决实际问题时,常见的增长率问题的解析式可以表示为y=N(1+p)x(其中N为基础数,p为增长率,x为时间)的形式.有关人口增长、银行利率、细胞分裂等增长率问题常用指数函数模型表示.
探究点二　对数函数模型
变式 某公司制定了一个激励销售人员的奖励方案:当销售利润不超过8万元时,按销售利润的15%进行奖励;当销售利润超过8万元时,若超出A万元,则超出部分按lg5(2A+1)进行奖励.记奖金为y(单位:万元),销售利润为x(单位:万元).(1)写出奖金y关于销售利润x的关系式;(2)如果业务员小江获得3.2万元的奖金,那么他的销售利润是多少万元?
[素养小结]直接以对数函数为模型的应用问题不是很多,此类问题一般是先给出对数函数模型,再利用对数运算性质求解.
探究点三　函数模型的选择
变式 某新型企业为获得更大利润,需不断加大投资,若年利润低于年投资成本的10%,则该企业就考虑转型,下表显示的是该企业几年来的年利润y(百万元)随年投资成本x(百万元)变化的一组数据:给出以下3个函数模型:①y=kx+b(k≠0);②y=abx(a≠0,b>0,且b≠1);③y=lga(x+b)(a>0,且a≠1).(1)选择一个恰当的函数模型来描述x,y之间的关系;(2)试判断该企业年利润超过6百万元时,该企业是否要考虑转型.
[素养小结]当一组数据所对应的函数关系不确定时,可根据题设条件,将这几个函数模型求出来,再根据题中的其他条件,对这几个函数模型的可靠性作出评估,选出与数据最吻合的函数模型.
探究点四　拟合函数的建立
例4 [2021·福建龙岩高一月考] 1766年,人类已经发现的太阳系中的行星有金星、地球、火星、木星和土星.德国的一位中学教师戴维·提丢斯在研究了各行星离太阳的距离(单位:AU,AU是天文学中计量天体之间距离的一种单位)的排列规律后,预测在火星和木星之间应该还有一颗未被发现的行星存在,并按离太阳的距离从小到大列出了如下表所示的数据:
受他的启发,意大利天文学家皮亚齐于1801年终于发现了位于火星和木星之间的谷神星.
(1)为了描述行星离太阳的距离y与行星编号之间的关系,根据表中已有的数据画出散点图,并根据散点图的分布状况,从以下三种模型中选出你认为最符合实际的一种函数模型(直接给出结论即可);①y=ax+b;②y=a·bx+c(b>1);③y=a·lgbx+c(b>1).(2)根据你的选择,由表中前几组数据求出函数解析式,并用剩下的数据检验模型的吻合情况;(3)请用你求得的模型,计算谷神星离太阳的距离.
解:(1)画出散点图如图所示:根据散点图可知,模型②最符合实际.
变式 为了估计山上积雪融化后对下游农田灌溉的影响,在山上建立了一个观察站,测量最大积雪深度x(单位:cm)与当年灌溉面积y(单位:公顷).现有连续10年的实测资料,如下表所示.
(1)根据表中数据画出散点图;(2)建立一个能基本反映灌溉面积y随最大积雪深度x变化的函数模型,并画出图像;(3)根据所建立的函数模型,估计若今年最大积雪深度为25 cm,则可以灌溉土地多少公顷?
解:(1)作出散点图如图(甲)所示:
这样,得到一个函数模型y=2.2+1.8x,作出函数图像如图(乙)所示,可以发现,这个函数模型与已知数据的拟合程度较好,这说明它能较好地反映灌溉面积与最大积雪深度的关系.(3)由(2)得到的函数模型为y=2.2+1.8x,则当x=25时,y=2.2+1.8×25=47.2,即当最大积雪深度为25 cm时,估计可以灌溉土地47.2公顷.
[素养小结]建立拟合函数与预测的基本步骤
拟合函数模型的应用题的解题步骤(1)作图:根据已知数据,画出散点图.(2)选择函数模型:一般是根据散点图的特征,联想哪些函数具有类似的图像特征,找几个比较接近的函数模型尝试.(3)求出函数模型:求出(2)中找到的几个函数模型的解析式.(4)检验:将(3)中求出的几个函数模型进行比较、验证,得出最合适的函数模型.
例 经多次实验得到某种型号的汽车每小时耗油量Q(单位:L)、百公里耗油量W(单位:L)与速度v(单位:km/h)(40≤v≤120)的数据如下表:为描述Q与v的关系,现有以下三种模型供选择:Q(v)=0.5v+a,Q(v)=av+b,Q(v)=av3+bv2+cv.(1)请填写表格空白处的数据,选出你认为最符合实际的函数模型,并求出相应的函数解析式;(2)已知某高速公路共有三个车道,分别是外侧车道、中间车道和内侧车道,车速范围分别是[60,90),[90,110),[110,120](单位:km/h),问:该型号汽车在哪个车道以什么速度行驶时W最小?
解:(1)表格空白处填入的数据见下表:故选择函数模型为Q(v)=av3+bv2+cv,
1.“红豆生南国,春来发几枝?”如图4-5-5给出了红豆生长时间t(月)与枝数y(枝)的散点图,那么对红豆生长时间与枝数的关系拟合最好的函数模型是(　　)　　　　　　 　　　　　　 　　　　　　 A.y=t3 B.y=lg2tC.y=2t D.y=2t2
[解析] 由散点图知指数函数模型拟合效果最好.
2.某种植物生长发育的数量y与时间x的关系如下表:则下面的函数关系式中,拟合效果最好的是(　　)A.y=2x-1B.y=x2-1C.y=2x-1D.y=1.5x2-2.5x+2
[解析] 将三组数据代入各选项的函数关系式中,三组数据均与D项的函数关系式吻合,故选D.
3.甲、乙两人在一次赛跑中,从同一地点出发,路程s与时间t的函数关系如图4-5-6所示,则下列说法正确的是(　　)A.甲比乙先出发B.乙比甲跑的路程多C.甲、乙两人的速度相同D.甲比乙先到达终点
[解析] 从图中直线可以看出,甲对应直线的斜率大于乙对应直线的斜率,s甲=s乙,所以甲、乙同时出发,跑了相同的路程,甲的速度比乙大,甲比乙先到达终点.故选D.
4.[2021·广州天河区高一期末] 某人喝了一定量的酒后,其血液中的酒精含量上升到0.8 mg/mL,此时他停止饮酒,其血液中的酒精含量以每小时20%的速度减少,经过n小时后他血液中的酒精含量在0.2 mg/mL以下,则n的最小整数值为(　　)(参考数据:lg 2≈0.30,lg 3≈0.48)A.6B.7C.8D.9