18.1.1 第1课时 平行四边形的边角的特征 人教版八年级数学下册教学课件

这是一份18.1.1 第1课时 平行四边形的边角的特征 人教版八年级数学下册教学课件，共21页。

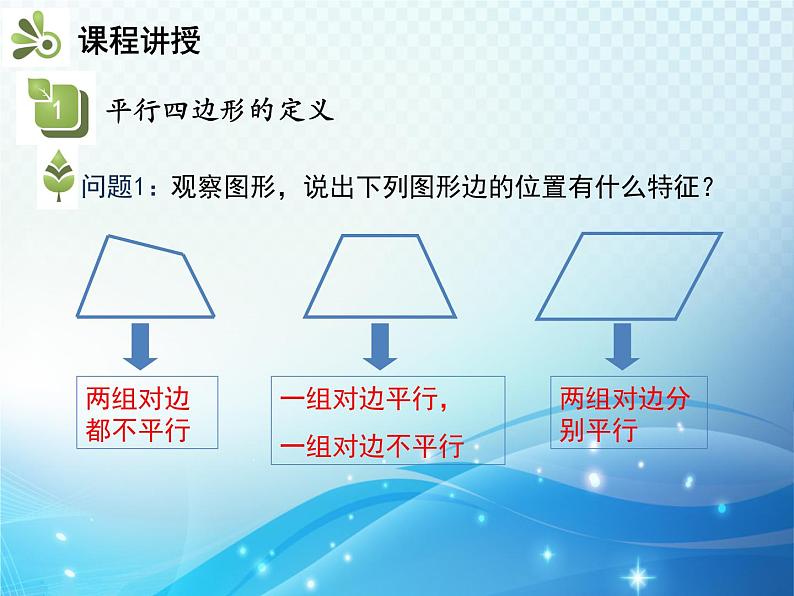
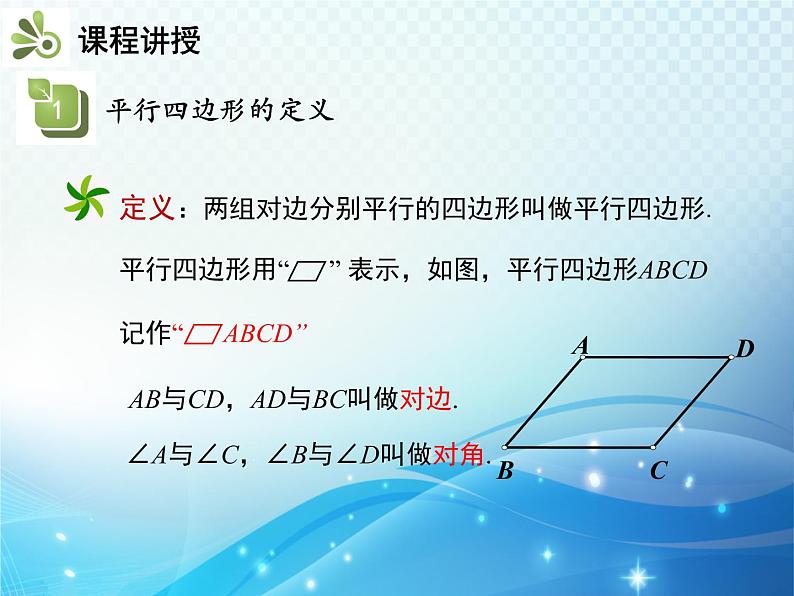
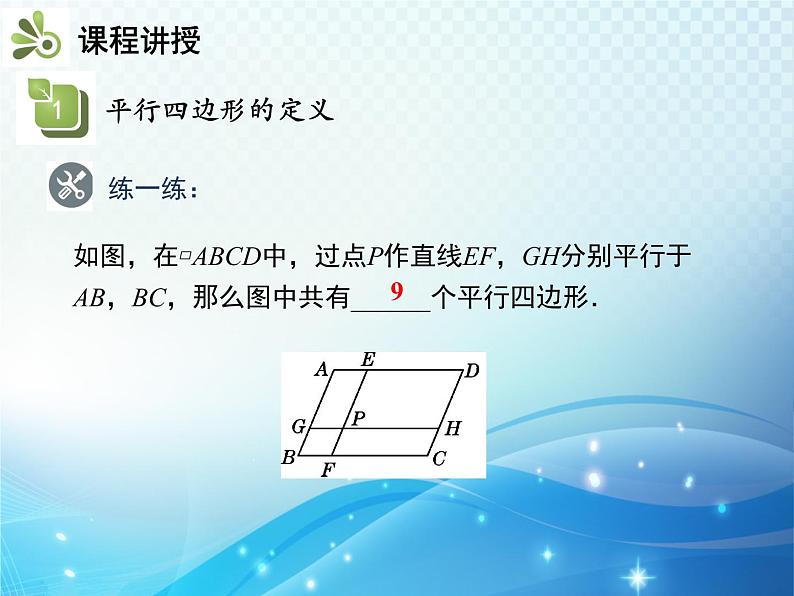
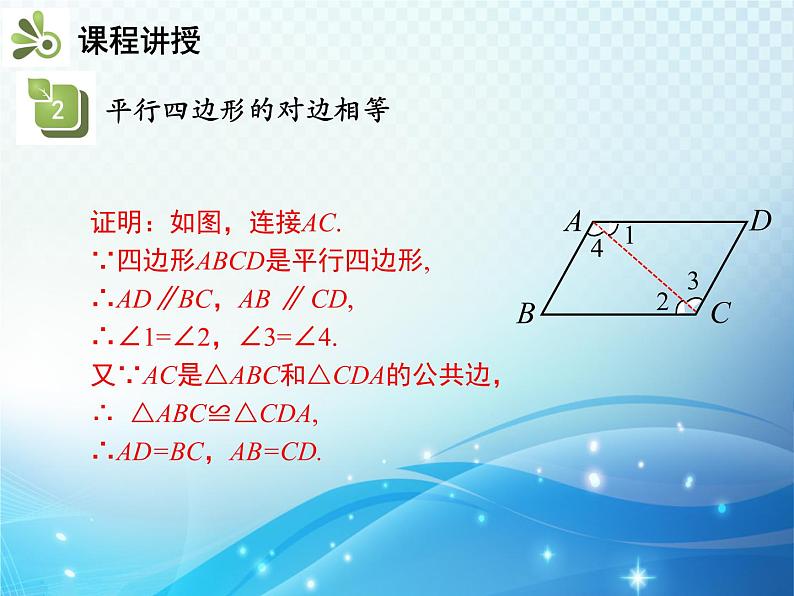
知识要点1.平行四边形的定义2.平行四边形的对边相等3.平行四边形的对角相等4.平行线间的距离平行四边形是生活中常见的图形.两组对边都不平行一组对边平行，一组对边不平行两组对边分别平行观察图形，说出下列图形边的位置有什么特征？定义：两组对边分别平行的四边形叫做平行四边形.平行四边形用“ ” 表示，如图，平行四边形ABCD记作“ ABCD”AB与CD，AD与BC叫做对边.∠A与∠C，∠B与∠D叫做对角.如图，在▱ABCD中，过点P作直线EF，GH分别平行于AB，BC，那么图中共有______个平行四边形． 9练一练：证明：如图，连接AC.∵四边形ABCD是平行四边形,∴AD∥BC，AB ∥ CD,∴∠1=∠2，∠3=∠4.又∵AC是△ABC和△CDA的公共边，∴ △ABC≌△CDA,∴AD=BC，AB=CD.1432 归纳：平行四边形的性质：平行四边形对边平行，平行四边形对边相等.数学表达式：如图，∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC，AB＝CD，AD＝BC.练一练： 在▱ ABCD 中，已知AB=5，BC=3，求它的周长.如图，因为四边形ABCD是平行四边形，所以CD＝AB＝5，AD＝BC＝3，所以▱ABCD的周长为AB＋BC＋CD＋AD＝5＋3＋5＋3＝16.证明：如图，连接AC.∵四边形ABCD是平行四边形,∴AD∥BC，AB ∥ CD,∴∠1=∠2，∠3=∠4.又∵AC是△ABC和△CDA的公共边，∴ △ABC≌△CDA,∴∠B=∠D.请同学们自己证明∠BAD =∠DCB.1432 归纳：平行四边形的性质：平行四边形的两组对角分别相等，邻角互补.数学表达式：如图，∵四边形ABCD是平行四边形， ∴∠A＝∠C，∠B＝∠D， ∠A＋∠B＝180°，∠B＋∠C＝180°，∠C＋∠D＝180°，∠A＋∠D＝180°.例 如图，在▱ABCD中，已知∠A＋∠C＝120°，求平行四边形各角的度数． 解：在▱ABCD中，∠A＝∠C，∠B＝∠D. ∵∠A＋∠C＝120°，∴∠A＝∠C＝60°. ∵∠D＝180°－∠A＝180°－60°＝120°. ∴∠B＝∠D＝120°.练一练：(中考·衢州)如图，在▱ABCD中，M是BC延长线上的一点.若∠A＝135°，则∠MCD的度数是(　　) A．45° B．55° C．65° D．75°A例 如图 ，在▱ ABCD 中，DE⊥AB，BF⊥CD， 垂足分别为E，F.求证：DE=BF.∵四边形ABCD是平行四边形，∴∠A=∠C，AD=CB.又 ∵∠AED=∠CFB = 90°，∴△ADE≌△CBF.∴ DE=BF.证明：如图，a∥b，若要使S△ABC＝S△DEF，需增加条件(　　) A．AB＝DE B．AC＝DF C．BC＝EF D．BE＝ADC练一练：1.直线a上有一点A，直线b上有一点B，且a∥b.点P在直线a，b之间，若PA＝3，PB＝4，则直线a，b之间的距离(　　) A．等于7 B．小于7 C．不小于7 D．不大于7D2.如图，D， E，F 分别在△ABC的边AB，BC，AC上，且DE∥AC,DF∥BC,EF∥AB，则图中有_____个平行四边形.3证明： ∵四边形ABCD是平行四边形， ∴ AB∥CD，AD=BC，∴ ∠CDE= ∠DEA，∠CFB= ∠FBA.又∵DE，BF分别平分∠ADC，∠ABC ，∴∠CDE= ∠ADE，∠CBF= ∠FBA，∴ ∠DEA= ∠ADE，∠CFB=∠CBF ，∴AE=AD ， CF=BC ，∴AE= CF.3.如图，在平行四边形ABCD中，DE平分∠ADC,BF平分∠ABC.求证:AE=CF. EF平行四边形的边、角特征平行四边形的定义平行线间的距离两组对边分别平行的四边形两组对边分别平行且相等平行四边形边的性质平行四边形角的性质两组对角分别相等，邻角互补两条平行线间的距离相等