中职数学高教版（中职）基础模块下册(2021)8.6 样本的均值和标准差优质教学课件ppt

这是一份中职数学高教版（中职）基础模块下册(2021)8.6 样本的均值和标准差优质教学课件ppt，共24页。PPT课件主要包含了学习目标，取偏差的绝对值，称为样本方差，方差甲乙，标准差甲乙，中位数是170m，众数是175m，乙机床质量更稳定，分层随机抽样的均值，抽象概括等内容，欢迎下载使用。

第八章 概率与统计初步 8.6 样本的均值和标准差
在初中，我们用过“自然数集”“有理数集”等表述，这里的“集”就是集合的简称，那么什么是集合呢？
知识回顾：在初中，我们学习过哪些统计量呢？
一. 样本的数字特征：
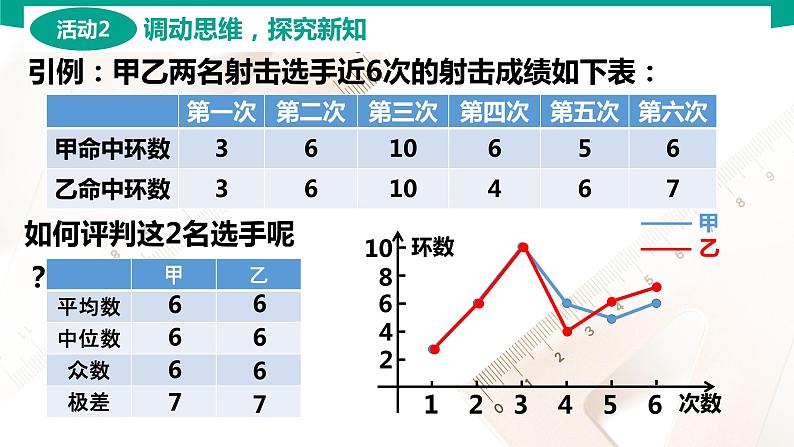
如何评判这2名选手呢？
引例：甲乙两名射击选手近6次的射击成绩如下表：
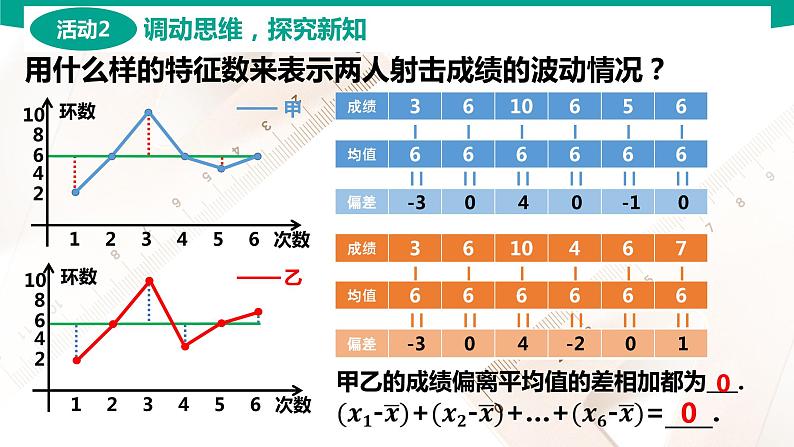
用什么样的特征数来表示两人射击成绩的波动情况？
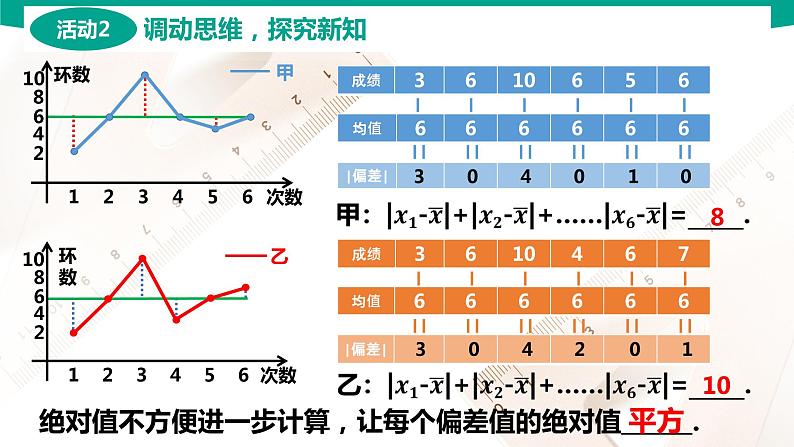
甲乙的成绩偏离平均值的差相加都为___.
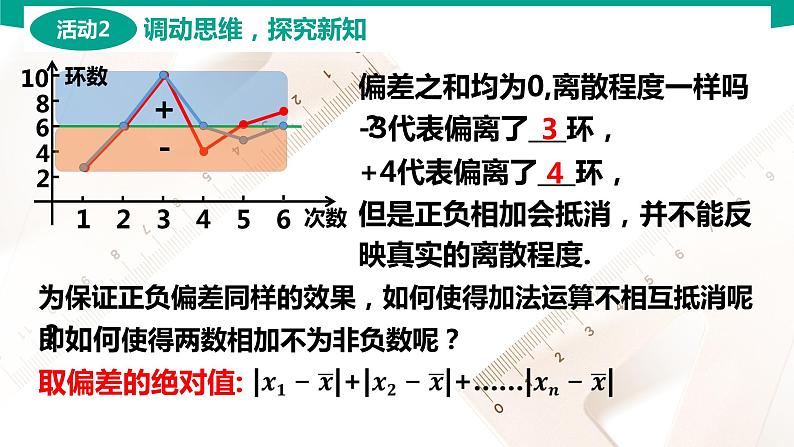
偏差之和均为0,离散程度一样吗？
-3代表偏离了___环，
+4代表偏离了___环，
但是正负相加会抵消，并不能反映真实的离散程度.
为保证正负偏差同样的效果，如何使得加法运算不相互抵消呢？
即如何使得两数相加不为非负数呢？
绝对值不方便进一步计算，让每个偏差值的绝对值______.
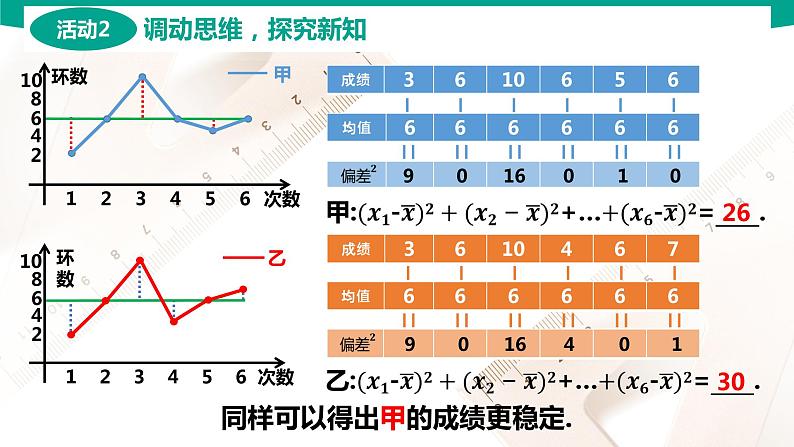
同样可以得出甲的成绩更稳定.
思考：如果甲继续射击，会有什么情况呢？
思考：继续用偏差的平方之和刻画波动性公平吗？
但是样本方差夸大了数据的离散程度，且原成绩的单位是环，平方之后的单位不好解释，因此常常用方差的算术平方根来表示个体与均值之间的偏离程度，称为样本标准差，即：
方差用____表示，标准差用____表示.
甲的方差是： 乙的方差是：
如何评判甲乙两名选手？
甲乙两人的平均数、众数、中位数、极差都相同.
甲的标准差是： 乙的标准差是：
相对于乙，甲的成绩更稳定.
例1. 在一次中学生田径运动会上，参加男子跳高的14名运动员的成绩如表所示：
分别求这些运动员的平均数(精确到0.01)、中位数、众数.
例2. 甲、乙两机床同时加工直径为100 cm的零件，为检验质量，各从中抽取6件测量，数据为：甲：99 100 98 100 100 103 乙：99 100 102 99 100 100(1). 分别计算两组数据的平均数、方差、标准差；(2). 根据计算结果判断哪台机床加工零件的质量更稳定．
例4. 某歌手电视大赛中，七位评委为甲选手打出了如下分数7.9、8.1、8.4、8.5、8.5、8.5、9.9，计算甲得分的平均数和方差(精确到0.01).
总结：对抽象数据进行整体代换
换个问法：七位评委为甲选手打出的最低分为7.9，最高分为9.9，且七位评委打出的平均分为8.54，求去掉一个最低分和最高分之后甲选手得分的平均分(精确到0.01).
三种收入人群所占的比重不同，所以这样计算不合理
思考：当不知道样本中每个数据，只知道分层随机抽样中各层的平均数，以及各层所占的比例(权重)，如何计算样本的平均数呢？
例如：某公司高收入员工月平均工资是11000元，中等收入员工月平均工资是6500元，低收入员工月平均工资是2900元，能否认为该公司员工的月平均工资收入是：
例如：某公司高收入员工(有n1人)月平均工资是11000元，中等收入员工(有n2人)月平均工资是6500元，低收入员工(有n3人)月平均工资是2900元，问：该公司员工的月平均工资收入是?
总的平均数等于相应分层样本的平均数与其权重乘积之和.
例5. 某单位共有员工100人，其中年轻人有20人，平均年薪为5万元，中年人有80人，平均年薪为8万元，则该单位员工的平均年薪为(　 ).A. 5万元 B. 8万元 C. 6.5万元 D. 7.4万元
例7. 如图，频率分布直方图如下，
(2).该组数据的平均数是______.(同组数据取该组区间中间值)
0.005×10×45+0.015×10×55+0.025×10×65+0.035×10×75++0.010×10×85+0.010×10×95=71.01(分)
(1). a=________.
(0.005+0.01×2+a+0.025+0.035)×10=1
3. 方差和标准差的表示及计算公式：
1. 样本的数字特征：
平均数、众数、中位数、极差、方差、标准差.