初中数学湘教版八年级下册2.2.2平行四边形的判定授课课件ppt

这是一份初中数学湘教版八年级下册2.2.2平行四边形的判定授课课件ppt，共13页。PPT课件主要包含了AB∥CD，ADBC，∠A∠C，知识回顾，抽象成几何作图，新知探究，∠AOB∠COD，于是AB∥DC，同理BC∥AD，又OEOF等内容，欢迎下载使用。

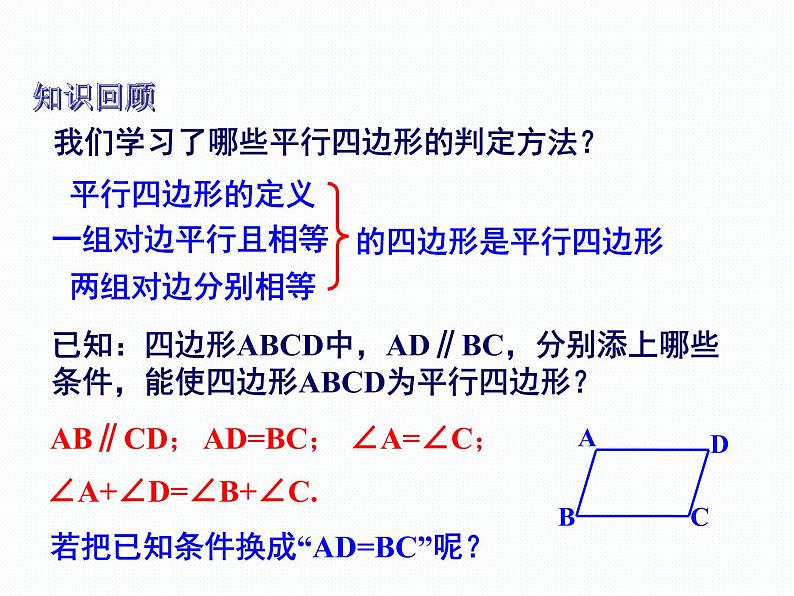
我们学习了哪些平行四边形的判定方法？
已知：四边形ABCD中，AD∥BC，分别添上哪些条件，能使四边形ABCD为平行四边形？
∠A+∠D=∠B+∠C.
若把已知条件换成“AD=BC”呢？
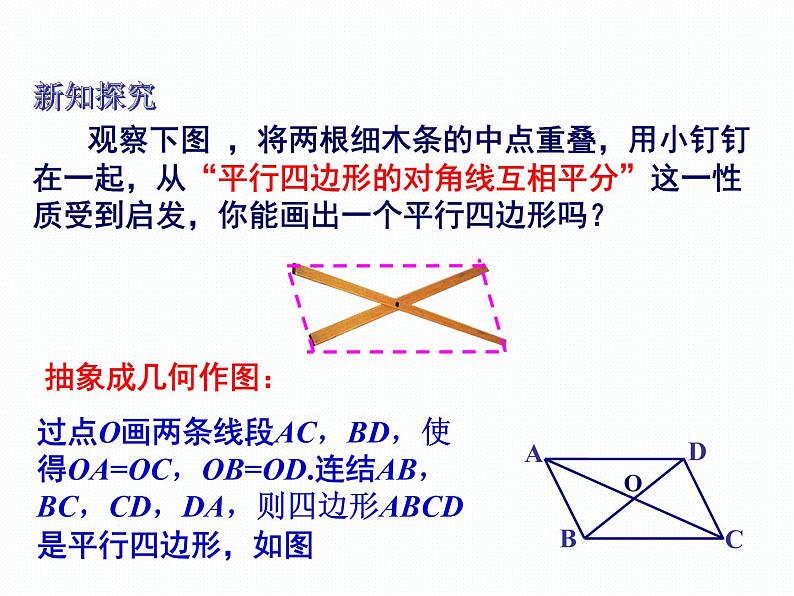
观察下图 ，将两根细木条的中点重叠，用小钉钉在一起，从“平行四边形的对角线互相平分”这一性质受到启发，你能画出一个平行四边形吗？
过点O画两条线段AC，BD，使得OA=OC，OB=OD.连结AB，BC，CD，DA，则四边形ABCD是平行四边形，如图
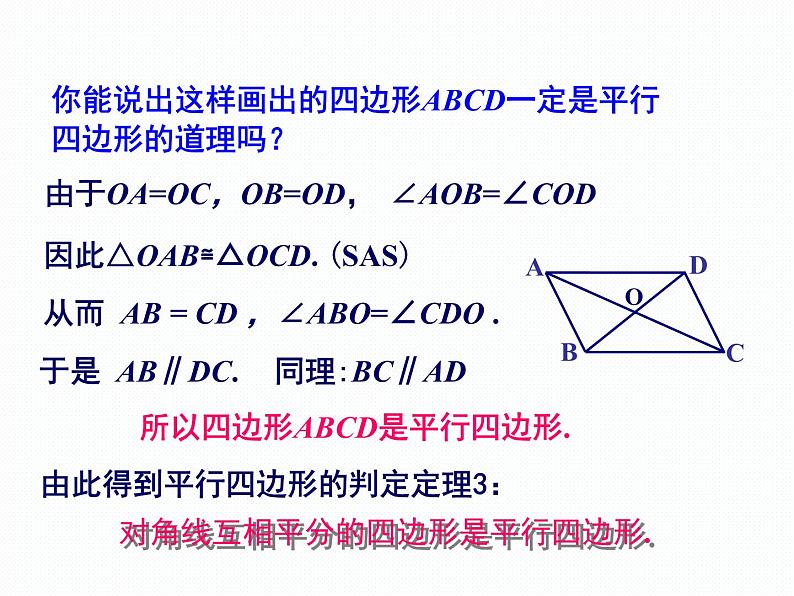
你能说出这样画出的四边形ABCD一定是平行四边形的道理吗？
由于OA=OC，OB=OD，
从而 AB = CD ，∠ABO=∠CDO .
所以四边形ABCD是平行四边形.
因此△OAB≌△OCD. (SAS)
对角线互相平分的四边形是平行四边形.
由此得到平行四边形的判定定理3：
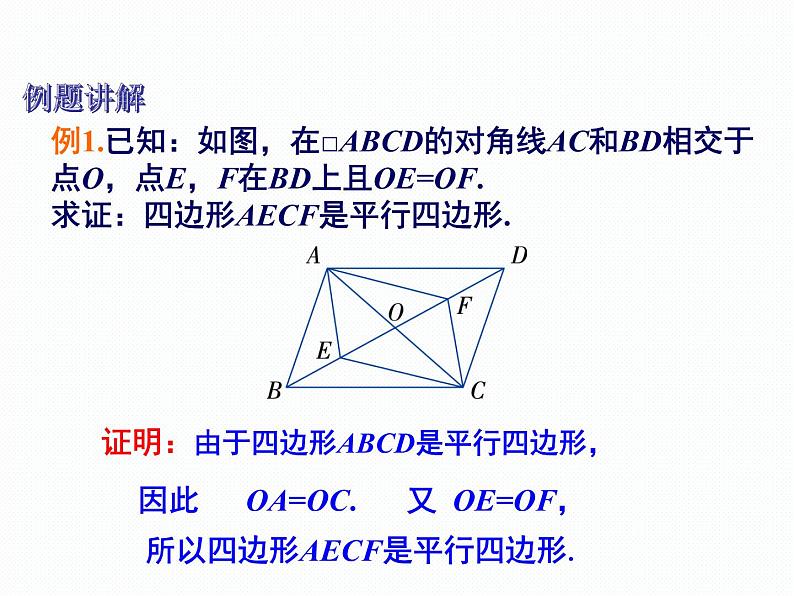
例1.已知：如图，在□ABCD的对角线AC和BD相交于点O，点E，F在BD上且OE=OF.求证：四边形AECF是平行四边形.
证明：由于四边形ABCD是平行四边形，
因此 OA=OC.
所以四边形AECF是平行四边形.
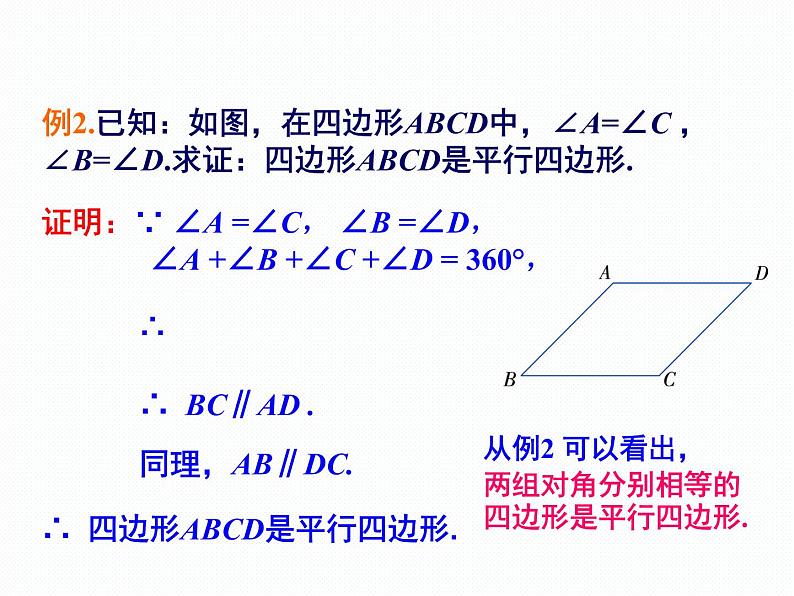
例2.已知：如图，在四边形ABCD中，∠A=∠C ，∠B=∠D.求证：四边形ABCD是平行四边形.
证明：∵ ∠A =∠C， ∠B =∠D， ∠A +∠B +∠C +∠D = 360°，
∴ 四边形ABCD是平行四边形.
从例2 可以看出， 两组对角分别相等的四边形是平行四边形.
例3.如图，在□ABCD中，点E、F是对角线AC上两点，且AE=CF.求证：四边形BFDE是平行四边形
∴四边形BEDF是平行四边形。
证明：∵四边形ABCD是平行四边形,
∴AB//CD，AB=CD,
∴∠BAE=∠DCF,
∵AE=CF，∴△ABE≌△CDF，
∴BE=DF，∠AEB=∠CFD，∴∠BEF=∠DFE,
∴四边形BFDE是平行四边形（对角线互相平分的四边形是平行四边形）．
证明：连结BD，交AC于点O
∵四边形ABCD是平行四边形 ∴OB＝OD，OA＝OC（平行四边形的对角线互相平分）
∵AE＝FC，∴OE＝OF，
∴∠EBF=∠FDE.
1.两组邻边分别相等的四边形一定是平行四边形吗？ 如果是，请说明理由；如果不是，请举出反例.
2.一组对边相等，另一组对边平行的四边形一定是平行四边形吗？如果是，请说明理由；如果不是，请举出反例.
1.如图，把△ABC的中线AD延长至E，使得DE=AD，连接EB，EC .求证：四边形ABEC是平行四边形.
证明：由已知BD=CD, DE=AD.
2.如图，□ABCD的对角线相交于点O，直线MN经过点O，分别与AB ，CD交于点M，N ，连接AN，CM.求证：四边形AMCN是平行四边形.
证明： ∵ □ABCD，∴ OA=OC, AB∥DC.
∴ 四边形AMCN是平行四边形.
∴ ∠BAC =∠ACD.
又 ∵∠AOM =∠CON,
∴ △AOM≌△CON. (ASA)
∴ AM=CN. 又∵ AM∥CN，
延长DE到F，使EF=DE，连接FC、DC、AF
4.□ABCD中，AF=CH，DE=BG，求证： EG和HF互相平分．
证明：△AEF≌△CGH（SAS）
同理可证：FG=HE
∴ 四边形EFGH是平行四边形 ∴ EG和HF互相平分
可证：四边形ADCF和四边形DBCF都是平行四边形。
通过这节课的学习，需要我们熟练掌握平行四边形的性质和判定并能灵活运用其解决相关的计算与证明。
作业：p50 A 6 B 8、9、10