初中数学湘教版八年级下册2.5.2矩形的判定授课ppt课件

这是一份初中数学湘教版八年级下册2.5.2矩形的判定授课ppt课件，共17页。PPT课件主要包含了平行四边形，四边形，新知探究，矩形性质，疑问升级，知识小结，我们来进行证明，总结矩形的判定方法，例题讲解，∵DF平分∠BDC等内容，欢迎下载使用。
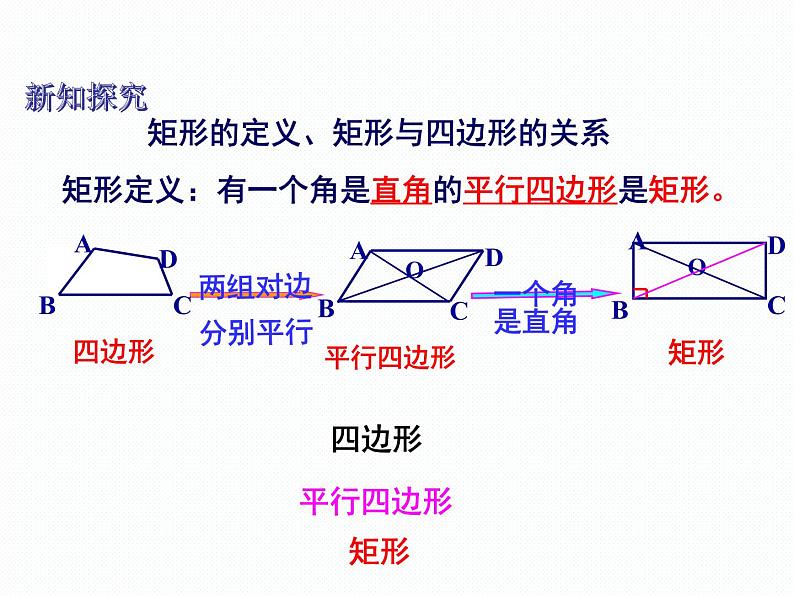
矩形定义：有一个角是直角的平行四边形是矩形。
矩形的定义、矩形与四边形的关系
2．矩形是平行四边形的特例，所以它具备平行四边形的一切性质。
3．矩形的四个角都是直角。
4．矩形的对角线相等。
或者说:矩形的对角线相等且互相平分.
1．矩形是四边形,所以它具备四边形的一切性质。
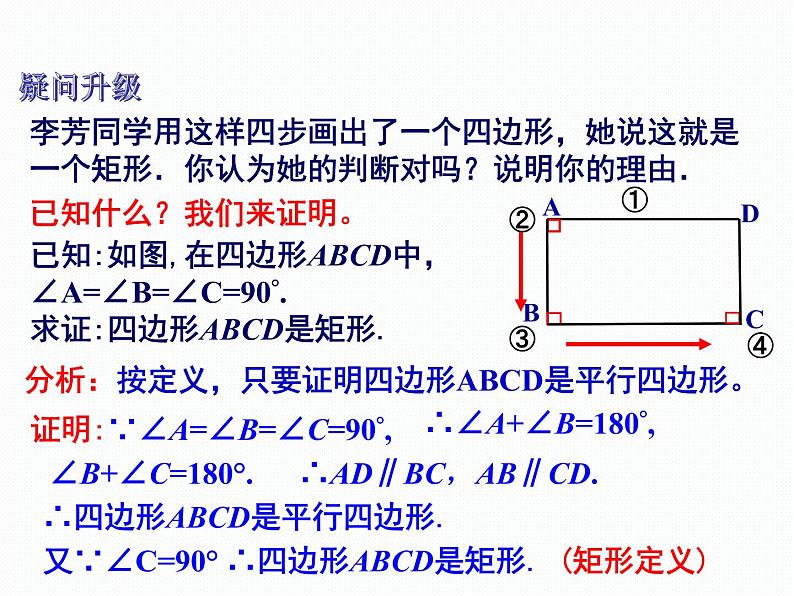
李芳同学用这样四步画出了一个四边形，她说这就是一个矩形．你认为她的判断对吗？说明你的理由．
已知:如图,在四边形ABCD中，∠A=∠B=∠C=90°.求证:四边形ABCD是矩形.
已知什么？我们来证明。
分析：按定义，只要证明四边形ABCD是平行四边形。
证明:∵∠A=∠B=∠C=90°,
∴∠A+∠B=180°,
∴AD∥BC，AB∥CD.
∠B+∠C=180°.
∴四边形ABCD是平行四边形.
又∵∠C=90° ∴四边形ABCD是矩形. (矩形定义)
三个角是直角的四边形是矩形.
由此，我们得到，矩形的判定定理：
三个角是直角的四边形，容易知道第四个角也是直角，
两个角是直角的四边形是矩形吗？
四边形中只有两个角是直角，我想到了下边的图形：
因此，两个角是直角的四边形不一定是矩形。
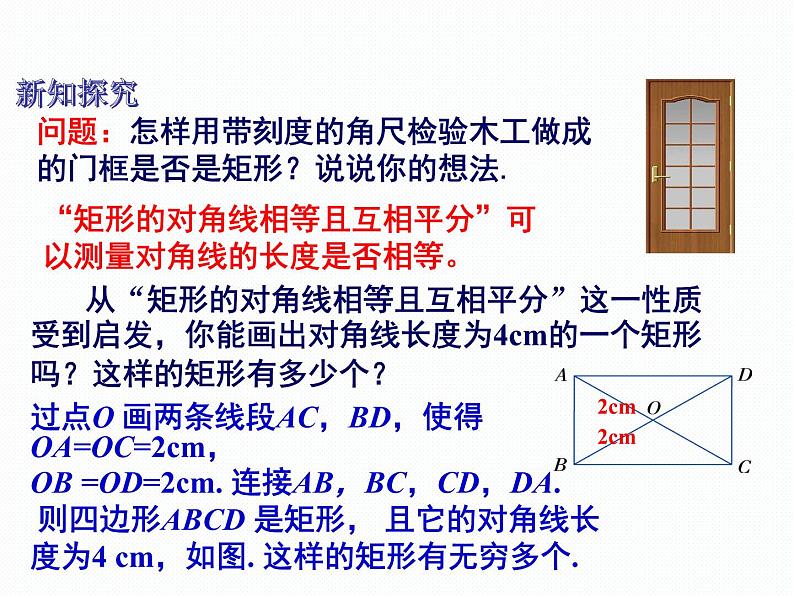
问题：怎样用带刻度的角尺检验木工做成的门框是否是矩形？说说你的想法.
从“矩形的对角线相等且互相平分”这一性质受到启发，你能画出对角线长度为4cm的一个矩形吗？这样的矩形有多少个？
“矩形的对角线相等且互相平分”可以测量对角线的长度是否相等。
过点O 画两条线段AC，BD，使得OA=OC=2cm，OB =OD=2cm. 连接AB，BC，CD，DA. 则四边形ABCD 是矩形， 且它的对角线长度为4 cm，如图. 这样的矩形有无穷多个.
如图，由画法可知，四边形ABCD的两条对角线互相平分，因此它是平行四边形，又已知其对角线相等，上述问题抽象出来就是：对角线相等的平行四边形是矩形吗？
在□ABCD中，由于AB=DC，AC=DB，BC=CB，
因此 △ABC≌△DCB. (SSS)
从而 ∠ABC=∠DCB.
又∠ABC+∠DCB =180°，
于是 ∠ABC=90°.
所以 □ABCD是矩形.
你能说出这样画出的四边形一定是矩形的道理吗？
由此得到矩形的判定定理：
对角线相等的平行四边形是矩形.
讨论：对角线相等的四边形是矩形吗？
对角线相等且互相平分的四边形是矩形.
1.有一个角是直角的平行四边形是矩形.2.有三个角是直角的四边形是矩形.3.对角线相等的平行四边形是矩形.或者:对角线相等且互相平分的四边形是矩形.
如何检查一个四边形的画框是否为矩形?
例1如图，在□ABCD中，它的两条对角线相交于点O（1）如果□ABCD是矩形，试问：△OBC是什么样的三角形？（2）如果△OBC是等腰三角形，其中OB=OC，那么□ABCD是矩形吗？
解：（1） ∵□ABCD是矩形，
∴ AC与DB相等且互相平分.
∴ △OBC是等腰三角形.
（2） ∵ △OBC是等腰三角形，其中OB = OC，
∴ AC = 2OC = 2OB = BD.
∴ □ABCD是矩形.(对角线相等的平行四边形是矩形）
例2.如图，O是□ABCD对角线的交点，AB=BC，作DE∥AC，CE∥BD，DE，CE交于点E． 求证:四边形CEDO是矩形．
证明: ∵ DE∥AC，CE∥BD，
∴DE∥OC，CE∥OD，
∴四边形CEDO是平行四边形．（平行四边形定义）
∵ AB=BC，O是AC的中点,
∴ BD⊥AC，即∠COD＝ 90°. （三线合一）
∴四边形CEDO是矩形．（矩形定义）
例3 如图，在△ABC中，点D在AB上，且AD=CD=BD，DE、DF分别是∠BDC、∠ADC的平分线。四边形FDEC是矩形吗?为什么?
答：四边形FDEC是矩形
证明：∵AD=CD=BD，
∴ ∠A=∠ACD, ∠B=∠DCB
∴ ∠ACD+∠DCB=90°
∴四边形FDEC是平行四边形
∴四边形FDEC是矩形
2、如图，直线EF∥MN，PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠ EAC、 ∠ MCA、 ∠ ACN、 ∠ CAF的角平分线，则四边形ABCD是（ ）A. 任意四边形 B. 平行四边形 C. 矩形 D. 不能确定
1、能够判断一个四边形是矩形的条件是（ ）A .对角线相等 B. 对角线垂直C.对角线互相平分且相等 D.对角线垂直且相等
3、矩形的一组邻边长分别是3cm和4cm，则它的对角线长是 cm.
4.判断:(1)有一个角是直角的四边形是矩形.( )(2)对角线相等的四边形是矩形. ( )(3)对角线相等且互相平分的四边形是矩形. ( )(4)四个角都相等的四边形是矩形. ( ) (5)对角互补的平行四边形是矩形 （ ）
5. 如图，在四边形ABCD中，∠A=∠B=∠C=∠D， 求证：四边形ABCD是矩形.
∴∠A=∠B=∠C=∠D= 90°
∵∠A+∠B+∠C+∠D= 360°
∴四边形ABCD是矩形.
6. 如图，在□ABCD中，对角线AC，BD相交于点O， ∠AOB = 60°，AB= 2，AC= 4，求□ABCD的面积.
∴△OAB是等腰三角形.
∴ △OAB是等边三角形.
又∠AOB = 60°，
∴ OA=OB=2， ∴ AC=BD=4.
∴ □ABCD是矩形.
7.如图 ，O是矩形ABCD的对角线AC与BD的交点，E、F、G、H分别是AO、BO、CO、OD上的点，且AE=BF=CG=DH。四边形EFGH是矩形吗？为什么？
8.如图，在□ ABCD中，以AC为斜边作Rt△ACE，又∠BED=90°,试说明四边形ABCD是矩形.
∵AE=BF=CG=DH
∴OE=OF=OG=OH
∴四边形EFGH是矩形
∵AC是□ ABCD的对角线，
矩形的判定方法:1.有一个角是直角的平行四边形是矩形.2.有三个角是直角的四边形是矩形.3.对角线相等的平行四边形是矩形.或者:对角线相等且互相平分的四边形是矩形.
作业：p63 A 3、4 B 7