资料中包含下列文件,点击文件名可预览资料内容



还剩27页未读,
继续阅读
成套系列资料,整套一键下载
- 第一单元 小数的意义和加减法——2022-2023学年四年级下册数学北师大版知识点总结+练习学案(教师版+学生版) 试卷 20 次下载
- 第三单元 小数乘法——2022-2023学年四年级下册数学北师大版知识点总结+练习学案(教师版+学生版) 试卷 18 次下载
- 第五单元 认识方程——2022-2023学年四年级下册数学北师大版知识点总结+练习学案(教师版+学生版) 试卷 16 次下载
- 第六单元 数据的表示和分析——2022-2023学年四年级下册数学北师大版知识点总结+练习学案(教师版+学生版) 试卷 15 次下载
- 第四单元 观察物体——2022-2023学年四年级下册数学北师大版知识点总结+练习学案(教师版+学生版) 试卷 15 次下载
第二单元 认识三角形和四边形——2022-2023学年四年级下册数学北师大版知识点总结+练习学案(教师版+学生版)
展开
这是一份第二单元 认识三角形和四边形——2022-2023学年四年级下册数学北师大版知识点总结+练习学案(教师版+学生版),文件包含第二单元认识三角形和四边形教师版2022-2023学年四年级下册数学北师大版知识点总结+练习学案docx、第二单元认识三角形和四边形学生版2022-2023学年四年级下册数学北师大版知识点总结+练习学案docx等2份试卷配套教学资源,其中试卷共43页, 欢迎下载使用。
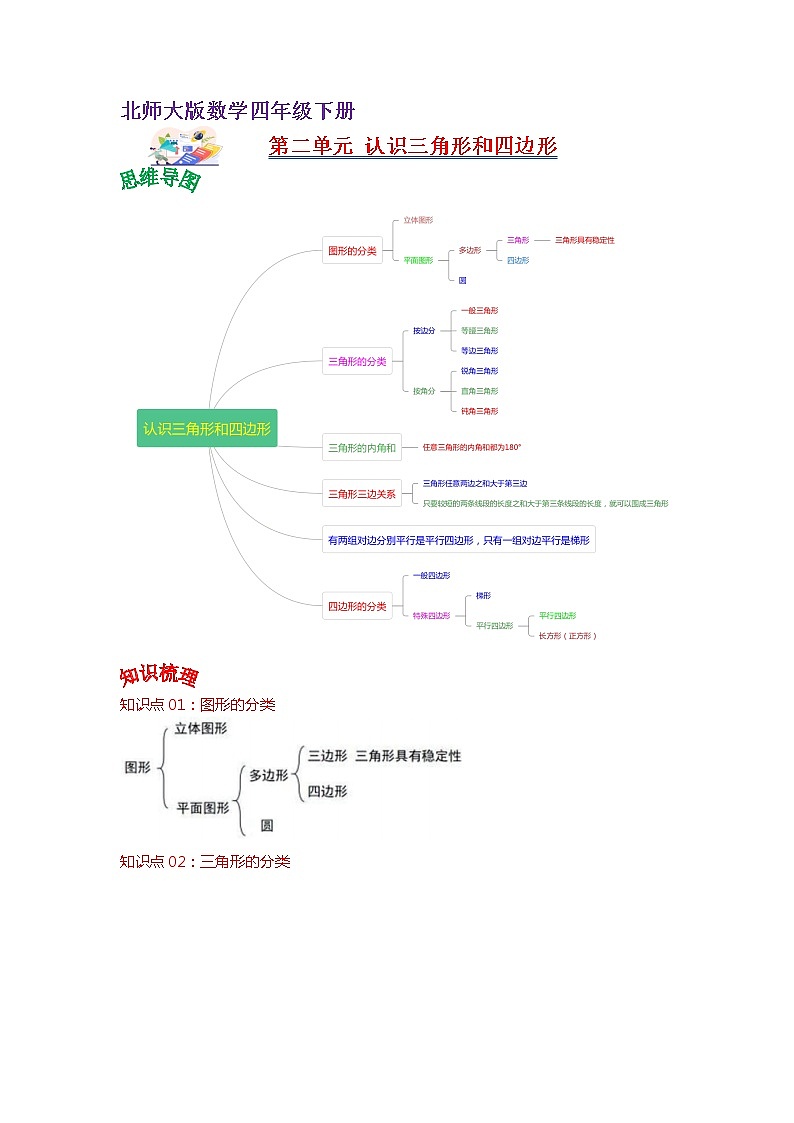
北师大版数学四年级下册
第二单元 认识三角形和四边形
知识点01:图形的分类
知识点02:三角形的分类
等边三角形是特殊的等腰三角形。
知识点03:三角形内角和
任意三角形的内角和都是 180°。
知识点04:三角形三边关系
1. 三角形任意两边之和大于第三边;
2. 判断三条线段能否围成三角形,只要较短的两条线段的长度之和大于第三条线段的长度,就可以围成三角形。
知识点05:平行四边形和梯形
有两组对边分别平行的四边形是平行四边形,只有一组对边平行的四边形是梯形。
知识点06:四边形的分类
考点01:图形的分类
【典例分析01】
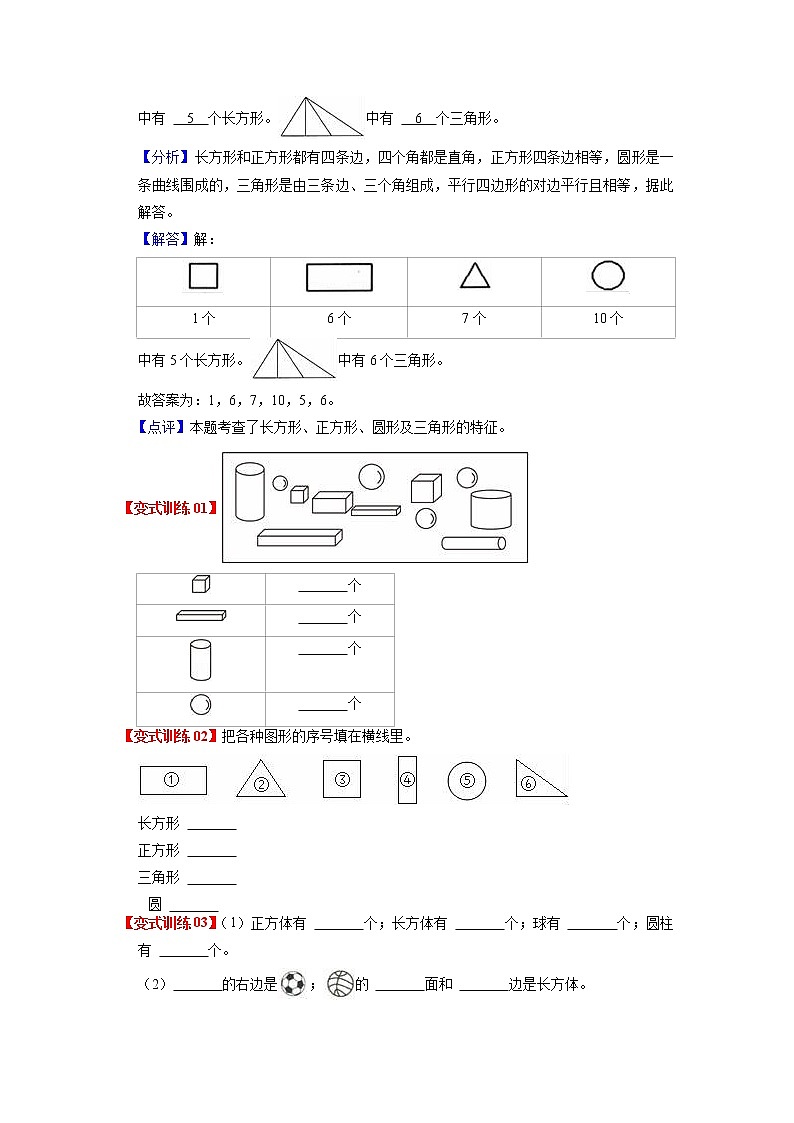
1 个
6 个
7 个
10 个
中有 5 个长方形。中有 6 个三角形。
【分析】长方形和正方形都有四条边,四个角都是直角,正方形四条边相等,圆形是一条曲线围成的,三角形是由三条边、三个角组成,平行四边形的对边平行且相等,据此解答。
【解答】解:
1个
6个
7个
10个
中有5个长方形。中有6个三角形。
故答案为:1,6,7,10,5,6。
【点评】本题考查了长方形、正方形、圆形及三角形的特征。
【变式训练01】
2 个
3 个
3 个
4 个
【分析】正方体:有8个顶点,6个面,每个面面积相等(或每个面都有正方形组成);长方体:有8个顶点,6个面,每个面都由长方形或相对的一组正方形组成;圆柱:上下两个面为大小相同的圆形,有一个曲面叫侧面;球:球是生活中最常见的图形之一,例如篮球、足球都是球,球是由一个面所围成的几何体。
【解答】解:
2个
3个
3个
4个
故答案为:2,3,3,4。
【点评】本题考查了长方体、正方体、圆柱及球的特征及认识。
【变式训练02】把各种图形的序号填在横线里。
长方形 ①④
正方形 ③
三角形 ②⑥
圆 ⑤
【分析】根据长方形、正方形、三角形和圆的特征进行分类识别。
【解答】解:把各种图形的序号填在横线里。
长方形 ①④
正方形 ③
三角形 ②⑥
圆 ⑤
故答案为:①④,③,②⑥,⑤。
【点评】本题考查了长方形、正方形、三角形和圆的特征,从而进行分类识别。
【变式训练03】(1)正方体有 2 个;长方体有 4 个;球有 2 个;圆柱有 5 个。
(2) 正方体 的右边是;的 下 面和 左 边是长方体。
(3)有一个图形,它的上面、右边都是圆柱,左边是长方体,这个图形可能是(),也可能是()(把正确的圈起来)。
【分析】根据立体图形的分类及识别方法、常见立体几何图形及性质,找出各种图形并填数。
【解答】解:(1)正方体有2个;长方体有4个;球有2个;圆柱有5个。
(2)正方体的右边是;的下面和左边是长方体。
(3)有一个图形,它的上面、右边都是圆柱,左边是长方体,这个图形可能是(),也可能是()。
故答案为:(1)2,4,2,5;(2)正方体,下,左;(3),。
【点评】此题考查了学生对立体图形的分类及识别的掌握情况。
考点02:三角形的分类、内角和及三边关系
【典例分析02】猜猜下面各是什么三角形。
【分析】任意三角形的内角和都是180度,利用180度减去已知的两个角的度数求出第三个角,根据第三角的特征判断三角形的种类;锐角三角形:最大角小于90°,直角三角形:最大角等于90°,钝角三角形:最大角大于90°;三条边相等的是等边三角形;直角三角形其余两个锐角的和等于直角。
【解答】解:180°﹣28°×2
=180°﹣56°
=124°,三角形最大的角是钝角,这是一个钝角三角形;
180°﹣36°﹣74°
=144°﹣74°
=70°
三角形的3个角都是锐角,因此三角形是锐角三角形。
如图:
【点评】本题考查了三角形按角、按边分类的方法。
【变式训练01】求下列三角形的度数。
【分析】三角形的内角和是180°,(1)(2)用180°减去2个已知角的度数就是第三个角的度数;(3)直角三角形中两个锐角的和是90度,利用90度减去已知的锐角就是另一个角的度数。
据此可解答。
【解答】解:(1)180°﹣55°+85°
=125°﹣85°
=40°
(2)180°﹣30°+35°)
=150°﹣35°
=115°
(3)90°﹣40°=50°
【点评】本题考查了学生对等腰三角形的特征及三角形内角和是180°的知识的掌握情况。
【变式训练02】星期天,明明从家出发到超市,走哪条路最近?最近的路与最远的路相差多远?
【分析】根据两点之间,线段最短,解答此题即可。
【解答】解:1100+1200﹣1300
=2300﹣1300
=1000(米)
答:明明从家出发到超市,走中间路最近,最近的路与最远的路相差1000米。
【点评】熟练掌握两点之间,线段最短,是解答此题的关键。
【变式训练03】请把下面这根纸条裁成3段围成一个三角形。先画一画,再标一标。每段的长度分别是 9 cm、 8 cm、 3 cm。
【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可。
【解答】解:由题意,符合题意的三角形各边可以为:9厘米、8厘米、3厘米。
故答案为:9,8,3。(答案不唯一)。
【点评】围成三角形中任意两条边的和大于第三边,即最长边要小于总长度的一半,是判断三条线段能否围成一个三角形的关键。
考点03:四边形的分类
【典例分析03】选择下面的小棒(每根不能折断),摆出长方形和正方形。
(1)选择 4 根 2 厘米的小棒就能摆出一个正方形。
(2)选择 2 根 3 厘米和 2 根 1 厘米的小棒,就能摆出一个长方形,请把这个长方形画在下面的方格纸上。(下面方格纸中每个小正方形的边长表示1厘米)
【分析】(1)有一组邻边相等且一个角是直角的平行四边形叫做正方形,正方形四条边相等;
(2)长方形的4个内角都是直角,长方形对边相等,据此选择画图。
【解答】解:(1)选择4根2厘米的小棒就能摆出一个正方形。
(2)选择2根3厘米和2根1厘米的小棒,就能摆出一个长方形。
如图:
故答案为:4,2;2,3;2,1。
【点评】本题考查了正方形和长方形的特征及画法。
【变式训练01】按顺序(A→B→C→D→A)连接各点,画出围成
的图形,围成的图形是 平行四边形 。
【分析】先按要求画图,然后进行判断即可。
【解答】解:按顺序(A→B→C→D→A)连接各点,画出围成的图形,围成的图形是平行四边形。
故答案为:平行四边形。
【点评】此题考查了平行四边形的特征。
【变式训练02】填一填。
【分析】根据长方形的特征,长方形有4条边,相对的边长度相等;据此解答即可。
【解答】解:
【点评】此题考查的目的是理解掌握长方形的特征及应用。
【变式训练03】根据图形之间的关系把“①四边形、②平行四边形、③长方形、④正方形、⑤梯形”这几个图形的序号填在下面对应的集合图中.
【分析】根据平行四边形、梯形、长方形和正方形的含义:两组对边都平行的四边形是平行四边形;一组对边平行而另一组对边不平行的四边形是梯形;有一个角是直角的平行四边形是长方形,一组邻边相等的长方形是正方形;可知:正方形是特殊的长方形,长方形是特殊的平行四边形;梯形和平行四边形都是四边形;据此解答即可。
【解答】解:如图所示:
【点评】本题考查的是正方形、平行四边形、梯形和长方形的定义,熟练掌握这些四边形的定义与性质是解答此题的关键。
一.选择题(共6小题)
1.如图三角形中,是直角三角形的是( )
A. B.
C.
【分析】分别计算出各个选项中另一个角的度数,再根据直角三角形的特征判断即可。
【解答】解:A.180°﹣40°﹣30°=110°,110°>90°,是钝角三角形,不符合题意;
B.180°﹣60°﹣30°=90°,90°=90°,是直角三角形,符合题意;
C.180°﹣40°﹣70°=70°,70°<90°,是锐角三角形,不符合题意。
故选:B。
【点评】本题考查了直角三角形的特征。
2.教室黑板的表面是( )。
A.圆形 B.长方形 C.三角形
【分析】根据长方形的特征选择即可。
【解答】解:教室黑板的表面是长方形。
故选:B。
【点评】本题主要考查了平面图形的分类及识别,解题的关键是掌握长方形的特征。
3.下图中不是同类的是( )
A. B. C. D.
【分析】文具盒、笔、墨水属于学习用品,帽子属于生活用品。据此做题。
【解答】解:文具盒、笔、墨水属于学习用品,帽子属于生活用品。
故选:A。
【点评】本题主要考查物体的分类,关键是利用生活常识做题。
4.将两个完全一样的直角三角形拼成一个大三角形,这个大三角形的内角和是( )
A.90° B.180° C.270° D.360°
【分析】只要是三角形,它的内角和就是180度,不管三角形是大还是小,它的内角和都是180度,据此解答.
【解答】解:根据三角形内角和定理,将两个完全一样的直角三角形拼成一个大三角形,这个大三角形的内角和是180°.
故选:B.
【点评】解答此题的主要依据是:三角形的内角和是180度.
5.下列三组线段,可以围成三角形的是( )
A. B.
C.
【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可。
【解答】解:A.5+5=10,所以不能够围成一个三角形;
B.4+5<10,所以不能围成三角形;
C.6+7=13,所以能围成三角形。
故选:C。
【点评】解决此题的关键是根据三角形的特性进行分析、解答。
6.课堂上,老师让每人准备两根长5厘米,两根长7厘米的小棒,然后拼成一个平行四边形。妙妙说:“我们组拼成了形状各异的平行四边形。”丁丁同意妙妙的意见。原因是( )
A.平行四边形容易变形
B.平行四边形的两组对边相等
C.平行四边形的两组对边平行
【分析】根据平行四边形不具有稳定性,解答此题即可。
【解答】解:拼成了形状各异的平行四边形,是因为平行四边形容易变形。
故选:A。
【点评】熟练掌握四边形的特性,是解答此题的关键。
二.填空题(共6小题)
7.我们的红领巾的形状是 三角 形,数学书的封面是 长方 形。
【分析】根据三角形及长方形的特征判断即可。
【解答】解:我们的红领巾的形状是三角形,数学书的封面是长方形。
故答案为:三角,长方。
【点评】本题主要考查了平面图形的分类与识别,解题的关键是熟记三角形及长方形的特征。
8.正方形和长方形都是由 4 条线段围成的图形,它们都有 4 个直角。
【分析】长方形是一种平面图形,长方形的四个角都是直角,同时长方形的对边互相平行且相等;
正方形是有一组邻边相等且一个角是直角的平行四边形。
【解答】解:正方形和长方形都是由4条线段围成的图形,它们都有4个直角。
故答案为:4,4。
【点评】此题考查了正方形和长方形的定义,要熟练掌握。
9.在长是10cm,宽是8cm的长方形里截一个最大的正方形,正方形的边长是 8 cm。
【分析】在长是10cm,宽是8cm的长方形里截一个最大的正方形,正方形的边长就等于长方形的宽,据此解答即可。
【解答】解:在长是10cm,宽是8cm的长方形里截一个最大的正方形,正方形的边长是8cm。
故答案为:8。
【点评】知道正方形的边长就等于长方形的宽,是解答此题的关键。
10.爷爷要用一根长1米的竹条扎一个等腰三角形的风筝骨架,风筝骨架三条边长可能是 3 dm、 3 dm和 4 dm。【长度保留整分米数】
【分析】在同一三角形中,有两条边相等的三角形是等腰三角形,已知要用一根长1米的竹条扎一个等腰三角形的风筝骨架,根据三角形的三边关系,任意两边的和必须大于第三边,但前提是必须有两条边相同,并且三角形三边的和是1米。
【解答】解:1m=10dm
3+3>4,且3+3+4=10;
所以风筝骨架三条边长可能是3dm、3dm和4dm。
故答案为:3,3,4(答案不唯一)。
【点评】本题考查了等腰三角形的特点和三角形的三边关系。
11.一个直角三角形,其中锐角是40°,另一个锐角是 50 °。
【分析】三角形的内角和等于180°,直角三角形有一个角等于90°,180°减去90°,再减去40°,即等于另一个锐角的度数。
【解答】解:180°﹣90°﹣40°
=90°﹣40°
=50°
答:另一个锐角是50°。
故答案为:50。
【点评】熟练掌握三角形内角和知识是解答本题的关键。
12.在按角为三角形分类时,如果只凭其中一个角就可以确定这个三角形的类型,那么它不可能是 锐 角三角形。
【分析】锐角三角形:三个角都小于90°;直角三角形:可记作Rt△.其中一个角必须等于90°;钝角三角形:有一个角大于90°,据此解答。
【解答】解:在按角为三角形分类时,如果只凭其中一个角就可以确定这个三角形的类型,那么它不可能是锐角三角形。
故答案为:锐。
【点评】本题考查了三角形按角分类的方法。
三.判断题(共5小题)
13.在一个三角形里最多有一个直角,至少有一个锐角。 ×
【分析】根据三角形的内角和等于180°,解答此题即可。
【解答】解:在一个三角形里最多有一个直角,至少有两个锐角。
所以题干说法是错误的。
故答案为:×。
【点评】熟练掌握三角形的内角和知识,是解答此题的关键。
14.一个梯形上底与下底间的距离处处相等. √ .
【分析】因为梯形的上下底是平行的,所以夹在两平行线之间的距离是处处相等,据此可知:梯形上底与下底间的距离处处相等的说法是正确的.
【解答】解:梯形上底与下底间的距离就是这个梯形的高,所以处处相等的说法是正确的.
故判断为:√.
【点评】此题考查梯形的特征,即上下底平行,还要明确夹在两平行线之间的距离是处处相等的.
15.是可以滚动的。 √
【分析】根据圆柱体的特征进行判断即可。
【解答】解:圆柱体是可以滚动的,原题说法正确。
故答案为:√。
【点评】本题考查圆柱体的特征。
16.一个三角形中有2个锐角,则这个三角形一定是锐角三角形。 ×
【分析】直角三角形有一个直角和2个锐角;钝角三角形有一个钝角和2个锐角,锐角三角形必须有3个锐角,据此解答。
【解答】解:一个三角形中有2个锐角,则这个三角形可能是锐角三角形,也可能是直角三角形或钝角三角形,原题说法错误。
故答案为:×。
【点评】本题考查了三角形的分类。
17.用分别长4cm、3cm、7cm的小棒可以围成一个三角形。 ×
【分析】求出较短两条边的和,与第三条边比较,比第三条边长就可以,否则构不成三角形
【解答】解:3+3=6(厘米)
6<7,构不成三角形,故原题错误。
故答案为:×。×
【点评】本题根据三角形任意两边之和大于第三边进行判断。
四.操作题(共1小题)
18.你能把各种图形整理一下吗?
图形
□
〇
△
个数
(1)一共有 22 个图形,最多的是 圆形 , 正方形 和 三角形 同样多。
(2)比□多 6 个,比〇少 2 个。
【分析】(1)根据长方形、正方形、三角形、圆的特征进行分类识别,数出相应的数量通过计算得出共有图形的个数,然后通过比较不同图形的数量解答;
(2)根据图形数量列式计算解答。
【解答】解:
图形
□
〇
△
个数
8
2
10
2
(1)一共有图形:8+2+10+2=22(个),最多的是圆形,正方形和三角形同样多。
(2)比□多:8﹣2=6(个),比〇少10﹣8=2(个)。
故答案为:22,圆形,正方形,三角形;6,2。
【点评】本题考查了长方形、正方形、三角形、圆的特征,从而进行分类识别。
五.应用题(共4小题)
19.猪八戒走一步的长度是8分米,有一间房子,房子的长是八戒走了10步的长度,宽是八戒走了5步的长度,你能知道这间房子的长和宽各是多少米吗?
【分析】用每步的长度乘步数,求出房子的长和宽,据此解答。
【解答】解:长:8×10=80(分米)
80分米=8米
宽:8×5=40(分米)
40分米=4米
答:这间房子的长大约是8米,宽大约是4米。
【点评】本题主要考查了整数乘法运用的理解和灵活运用情况。
20.用一根217厘米长的铁丝正好围成一个等腰梯形。梯形的上底是31厘米,下底是66厘米,它的一条腰长多少厘米?
【分析】等腰梯形的两腰相等,用一根217厘米长的铁丝正好围成一个等腰梯形,铁丝的总长减去上下底的长就是两腰的长,再除以2即可。
【解答】解:(217﹣31﹣66)÷2
=120÷2
=60(厘米)
答:它的一条腰长60厘米。
【点评】本题考查了等腰梯形的特征。
21.王老师准备了12厘米和6厘米的木棒各一根,现在他想拼成一个三角形,这个三角形第三边最长是多少厘米?最短是多少厘米?(取整厘米)
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:12+6=18(厘米)
12﹣6=6(厘米)
根据三角形的三边关系,因此三角形的第三边必须在6和118之间,因此最长是:18﹣1=17(厘米),最短是6+1=7(厘米)。
答:这个三角形第三边最长是17厘米,最短是7厘米。
【点评】本题考查了三角形的三边关系的应用。
22.王明做了一个等腰三角形风筝,它的顶角是76°,它的一个底角是多少度?
【分析】根据等腰三角形的两底角相等,和三角形的内角和等于180°,解答此题即可。
【解答】解:(180﹣76)÷2
=104÷2
=52(度)
答:它的一个底角是52度。
【点评】熟练掌握三角形的内角和知识和等腰三角形的性质,是解答此题的关键。
一.选择题(共5小题)
1.能向任意方向滚动的是( )
A. B.
C.
【分析】根据立体图形的分类及特征即可解答。
【解答】解:能向任意方向滚动的是球。
故选:C。
【点评】本题主要考查立体图形的特征等。
2.一个三角形最小的锐角是50度,这个三角形一定是( )三角形.
A.钝角 B.直角 C.锐角
【分析】由三角形的内角和求出另外两个角的和,再根据最小的内角是50°来判断其它两个角的情况.
【解答】解:180°﹣50°=130°;
另外两个角的和是130°,最小的内角是50°,
假设另外两个角中还有一个是50°,另一个就是:130°﹣50°=80°;
最大的内角最大只能是80°,所以这个三角形的三个角都是锐角,这个三角形一定是锐角三角形.
故选:C.
【点评】解决本题首先要能根据三角形的内角和是180°,求出另外角的度数可能的情况,并由此求解.
3.一个等腰三角形中,其中一底角是75度,顶角是( )
A.75度 B.45度 C.30度
【分析】因为等腰三角形的两个底角相等,其中一底角是75度,另一个底角也是75°,根据三角形的内角和是180°,所以用180°减去两个底角的度数就是顶角的度数。
【解答】解;180°﹣75°×2
=180°﹣150°
=30°
答:顶角是30°。
故选:C。
【点评】本题要根据等腰三角形的两个底角相等和三角形的内角和是180°这两个知识点解答。
4.璐璐用小棒围三角形,已经选了长5厘米和8厘米的各一根,第三根应该选( )厘米的小棒。
A.14 B.7 C.3 D.2
【分析】根据三角形的两边之和大于第三边,两边之差小于第三边,解答此题即可。
【解答】解:8﹣5<第三边<8+5
3<第三边<13
答:第三根小棒的长度最长不能超过12厘米,最短不少于4厘米,所以第三根应该选7厘米的小棒。
故选:B。
【点评】熟练掌握三角形的三边关系,是解答此题的关键。
5.图的长方形由铁丝围成,在a、b、c、d拐弯处做上记号“•”,再从其中一个拐弯点把铁丝剪开拉直,那么铁丝可能是( )
A. B.
C. D.
【分析】根据长方形的特征:由4条边围成,对边平行且相等,因为长方形两条长,两条宽,所以长方形拉直后,这根铁丝应该是分成长、宽、长、宽四段;由此结合选项进行选择即可。
【解答】解:如图的长方形由铁丝围成,在a、b、c、d拐弯处做上记号“•”,再从其中一个拐弯点把铁丝剪开拉直,那么铁丝可能是。
故选:C。
【点评】灵活掌握长方形的特征,是解答此题的关键。
二.填空题(共5小题)
6.
上面10个图形中,四边形有 6 个, 1 是正方形, 4、8 是长方形。
【分析】有4条边首尾相连的图形是四边形,最后找出正方形和长方形即可,据此解答。
【解答】解:上面10个图形中,四边形有6个,1是正方形,4、8是长方形。
故答案为:6,1,4、8。
【点评】本题考查了四边形的特征及分类,结合题意分析解答即可。
7.现有两根分别长3厘米和5厘米的小棒,如果再添一根小棒围成一个三角形。那么这根小棒最短应该是 3 厘米,最长是 7 厘米。(取整厘米数)
【分析】三角形的三条边中,任意两边之和大于第三边,任意两边之差小于第三边,由此解答即可。
【解答】解:三根小棒首尾相连围成一个三角形,已知其中两根小棒分别长3厘米和5厘米,因此它的第三边最长是3+5﹣1=7(厘米),最短是5﹣3+1=3(厘米)
答:小棒最短可能是3厘米,最长可能是7厘米。
故答案为:3;7。
【点评】本题考查了三角形的三边关系的应用。
8.一个等腰三角形的底角是45度,它的顶角是 90 度,这还是一个 直 角三角形:根据三角形的内角和可以推算出梯形内角和是 360 度。
【分析】根据等腰三角形的特征,等腰三角形的两个底角相等,三角形的内角和是180度,用三角形的内角和减去两个底角的度数就是顶角的度数。梯形可以分成两个三角形,所以梯形的内角和是360度。据此解答。
【解答】解:180°﹣45°﹣45°=90°
180°×2=360°
答:它的顶角是90°,还是一个直角三角形,梯形的内角和是360°。
故答案为:90,直,360。
【点评】此题考查的目的是理解等腰直角三角形的特征及应用,三角形的内角和及应用。
9.已知一个三角形的一个锐角是50°,另一个锐角是70°,第三个角是 60° 。这是一个 锐角 三角形。
【分析】三角形的内角和是180度,用180度减去已知的两个角的和就是第三个角的度数,进而根据最大角的度数判断三角形的类别。
【解答】解:180°﹣(50°+70°)
=180°﹣120°
=60°
最大角是70°,是锐角,所以这是一个锐角三角形。
答:第三个角是60°,这是一个锐角三角形。
故答案为:60°,锐角。
【点评】此题主要考查三角形的内角和是180度的灵活运用以及三角形的分类。
10.数一数。
2
6
5
2
2
【分析】长方形和正方形都有四条边,四个角都是直角,正方形四条边相等,圆形是一条曲线围成的,三角形是由三条边、三个角组成,平行四边形的对边平行且相等,据此解答。
【解答】解:如表:
2
6
5
2
2
故答案为:2,6,5,2,2。
【点评】本题考查了长方形、正方形、三角形、圆形及平行四边形的特征及认识。
三.判断题(共5小题)
11.羽毛球的形状是球。 ×
【分析】球是生活中最常见的图形之一,例如篮球、足球都是球,羽毛球的形状不是球,由此解答即可。
【解答】解:羽毛球的形状不是球,原题说法错误。
故答案为:×。
【点评】本题考查了球的特征。
12.在一个三角形的三个角中,如果只有两个角是锐角,那么这个三角形一定不是直角三角形。 ×
【分析】根据三角形的内角和是180°可知,如果一个三角形只有两个内角是锐角,则另外一个角可以是直角或钝角,则这个三角形可能是直角三角形,也可能是钝角三角形;解答即可。
【解答】解:由三角形的内角和是180°可知,如果一个三角形只有两个内角是锐角,则另外一个角可以是直角,也可以是钝角,
则这个三角形一定是直角或钝角三角形。所以原题说法错误。
故答案为:×。
【点评】此题主要考查三角形的内角和及三角形的分类。
13.一个三角形最少有两个锐角,最多有三个锐角. √ .
【分析】根据三角形的内角和等于180°,三个角中最多有一个直角或钝角,所以最少有两个锐角;而如果一个三角形中没有直角或钝角,则三个角就都是锐角,即最多有3个锐角,据此即可判断.
【解答】解:因为三角形的内角和等于180°,
所以三角形最多有一个直角或钝角,剩下的两个为锐角;
所以一个三角形中,最少有2个锐角;
如果一个三角形中没有直角或钝角,则三个角就都是锐角,
因此最多有3个锐角;
所以“一个三角形最少有两个锐角,最多有三个锐角”的是说法是正确的.
故答案为:√.
【点评】此题考查了三角形内角和定理的灵活应用.
14.从2厘米、3厘米、4厘米、6厘米的4根小棒中选三根围成一个三角形,有2种不同的选法。 √
【分析】根据三角形三条边之间的关系,在三角形中,任意两边之和大于第三边,任意两边之差小于第三边。据此解答即可。
【解答】解:因为2+3=5(厘米)
5厘米大于4厘米
所以用2厘米、3厘米、4厘米三根小棒可以围成一个三角形;
因为3+4=7(厘米)
7厘米大于6厘米
所以用3厘米、4厘米、6厘米三根小棒可以围成一个三角形;
因此,从2厘米、3厘米、4厘米、6厘米的4根小棒中选三根围成一个三角形,有2种不同的选法。
故答案为:√。
【点评】此题考查的目的是理解掌握三角形三条边之间的关系及应用。
15.正方形是特殊的长方形,长方形是特殊的平行四边形. √ .
【分析】根据平行四边形的意义,对边平行的四边形是平行四边形,长方形对边也平行,因此它属于平行四边形,即角为直角的特殊平行四边形;根据长方形的意义,两组对边平行,角为直角,根据正方形两组对边平行且相等,角为直角,即正方形是四条边都相等的特殊长方形.即正方形是特殊的长方形,长方形是特殊的平行四边形.
【解答】解:如图
正方形是四条边相等的特殊长方形
长方形是角为直角的特殊平行四边形
因此,正方形是特殊的长方形,长方形是特殊的平行四边形,这种说法正确.
故答案为:√.
【点评】根据平行四边形、长方形、正方形的意义或特征即可判定.
四.操作题(共3小题)
16.(1)请在下方右边空白处画一个与如图完全一样的直角梯形。
(2)在原图中画出:上底延长到E,连接EC后变成一个长方形。再想象填一填:如果把画好后的长方形AB边向上延长1厘米到F,并连接EF,又会变成 梯 形。
【分析】(1)根据要求,结合梯形的画法,画一个与如图完全一样的直角梯形即可。
(2)根据要求,上底延长到E,连接EC后变成一个长方形。
再想象填一填:如果把画好后的长方形AB边向上延长1厘米到F,并连接EF,又会变成梯形。
【解答】解:作图如下:
如果把画好后的长方形AB边向上延长1厘米到F,并连接EF,又会变成梯形。
故答案为:梯。
【点评】本题考查了梯形的特征及画法知识,结合题意分析解答即可。
17.在能拼成三角形的小棒下面画“☆”.(单位:厘米)
【分析】根据三角形的三边关系:三角形任意两边之和大于第三边,对各选项进行逐一分析即可.
【解答】解:A、5+4=9>6,能组成三角形;
B、4+4=8>6,能组成三角形;
C、2+3=5<7,不能组成三角形;
故答案为:
【点评】本题考查的是三角形的三边关系,即三角形任意两边之和大于第三边,任意两边之差小于第三边;实际判断时选取两条较短的边求和再与最大边进行比较即可.
18.在点子图上画一个锐角三角形.
【分析】三个角都是锐角的三角形是锐角三角形,由此画出即可.
【解答】解:
【点评】明确锐角三角形的含义,是解答此题的关键.
五.应用题(共2小题)
19.一块平行四边形的菜地,一条边长为8米,比另一条边短2米。围这块菜地需要多长的栅栏?
【分析】平行四边形的两组对边分别相等,据此求出相邻的两条边的和,再乘2即可得出平行四边形的周长,即围这块菜地需要的栅栏长。
【解答】解:(8+8+2)×2
=18×2
=36(米)
答:围这块菜地需要36米长栅栏。
【点评】此题主要考查平行四边形的周长的计算应用。
20.一个等腰三角的一个顶角是64°,它的一个底角是多少度?如果它的底角是64°,那么它的顶角是多少度?
【分析】三角形内角和等于180°,等腰三角形的两个底角相等;180°减顶角的度数,再除以2等于一个底角的度数;180°减两个底角的度数,等于顶角的度数;据此即可解答。
【解答】解:(180°﹣64°)÷2
=116°÷2
=58°
180°﹣64°×2
=180°﹣128°
=52°
答:一个等腰三角的一个顶角是64°,它的一个底角是58°;一个等腰三角底角是64°,它的顶角是52°。
【点评】本题主要考查学生对三角形的内角和及等腰三角形的特征的掌握和灵活运用。
一.选择题(共5小题)
1.(2021秋•黄陂区期末)下面( )搭得最稳。
A. B. C.
【分析】结合图中几何形体的特性,分析哪组搭得最稳。
【解答】解:A组将圆柱放在正方体放上,正方体与桌面、正方体与圆柱体的接触面都是一个平面,所以搭得较为稳当;
B组将长方体放在圆柱体上,圆柱体在桌面上容易沿侧面方向滚动,球也容易从圆柱上滚落下来;
C组将球放在正方体上,球在正方体上容易滚动滑落下来。
故选:A。
【点评】球容易向桌面四周滚动,圆柱容易沿侧面方向在桌面上滚动。
2.(2022秋•密云区期末)如图所示图中能正确表示锐角三角形、直角三角形、钝角三角形之间关系的是( )
A. B.
C.
【分析】三角形按角分,锐角三角形:三个角都小于90°;直角三角形:可记作Rt△.其中一个角必须等于90°;钝角三角形:有一个角大于90°,它们之间是并存的关系。
【解答】解:三角形按角分为锐角三角形、直角三角形和钝角三角形,它们的关系是。
故选:C。
【点评】本题考查了三角形按角分类的方法。
3.(2020春•嘉荫县期末)下列三组度数中,能组成三角形的是( )
A.50°,50°,50° B.60°,60°,60°
C.70°,70°,70°
【分析】根据三角形的内角和是180°,分析解答即可。
【解答】解:A.50°+50°+50°=150°,小于180°,不能组成三角形;
B.60°+60°+60°=180°,符合三角形内角和180°,可以组成三角形;
C.70°+70°+70°=210°,大于180°,不能组成三角形。
故选:B。
【点评】本题考查了三角形内角和知识,结合题意分析解答即可。
4.(2022春•城阳区期末)下面几组小棒,( )组小棒能围成三角形。(单位:cm)
A.7,7,7 B.10,2,12 C.3,5,10
【分析】依据三角形的两边之和大于第三边的特点,即可进行判断。
【解答】解:A、因为7+7>7,所以能围成三角形;
B、因为10+2=12,所以不能围成三角形;
C、因为3+5<10,所以不能围成三角形。
故选:A。
【点评】此题主要考查三角形的两边之和大于第三边的特点。
5.(2022秋•石景山区期末)如图所示图形中是四边形的是( )
A. B. C. D.
【分析】四边形就是四条线段围成的图形,有四条边,四个角,据此选择。
【解答】解:是四边形。
故选:D。
【点评】本题考查了四边形的特征。
二.填空题(共5小题)
6.(2021春•滁州期末)一个梯形上底长4厘米,下底长6厘米,高3厘米(如图)。如果将上底向一端延长2厘米,则变成一个 平行四边 形;如果将上底缩短4厘米,则变成一个 三角 形。
【分析】根据梯形的定义可知:梯形的两个底互相平行且不相等,如果将上底延长2厘米,则上底变成4+2=6厘米,与下底相等了,由此根据一组对边平行且相等的四边形是平行四边形,即可解答;
当上底缩短4厘米时,4﹣4=0,即上底缩为一个点,此时梯形变为三角形。
【解答】解:4+2=6(厘米)
则上底与下底相等,因为平行四边形的对边平行且相等,所以这个图形是平行四边形;
当上底缩短4厘米时,4﹣4=0,
即上底缩为一个点,此时梯形变为三角形。
故答案为:平行四边,三角。
【点评】此题考查了梯形与平行四边形的定义与性质的灵活应用:一组对边平行且相等的四边形是平行四边形,还考查了三角形的特点,结合题意解答即可。
7.(2021秋•新泰市期末)用小棒围成三角形,其中两根小棒分别长7厘米和5厘米,第三根小棒最长 11 厘米,最短 3 厘米,可以围成三角形。(填整厘米数)
【分析】根据三角形的三边关系:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可。
【解答】解:7+5=12(厘米)
最长:12﹣1=11(厘米)
7﹣5=2(厘米)
最短:2+1=3(厘米)
因此第三根小棒最长11厘米,最短3厘米。
故答案为:11,3。
【点评】此题关键是根据三角形的三边关系进行分析、解答。
8.(2022春•梁平区期末)一个三角形,其中两个内角的度数分别是58°、62°,第三个内角是 60 度;1个直角三角形,其中一个锐角是36°,另一个锐角是 54 度。
【分析】根据三角形的内角和等于180°,解答此题即可。
【解答】解:180﹣(58+62)
=180﹣120
=60(度)
180﹣90﹣36
=90﹣36
=54(度)
答:一个三角形,其中两个内角的度数分别是58°、62°,第三个内角是60度;1个直角三角形,其中一个锐角是36°,另一个锐角是54度。
故答案为:60;54。
【点评】熟练掌握三角形的内角和知识,是解答此题的关键。
9.(2022春•鄂伦春自治旗期末)红领巾是我们少先队员佩戴的标志,如果按角分它是一个 钝角 三角形,按边分它又是一个 等腰 三角形。
【分析】根据三角形的分类标准,以及红领巾的特点进行填空即可;三角形按角分为:钝角三角形、直角三角形和锐角三角形,有一个角是钝角的三角形是钝角三角形,有一个角是直角的三角形是直角三角形,三个角都是锐角的三角形是锐角三角形;按边分为:等腰三角形、等边三角形,等腰三角形的两腰相等,两个底角也相等;等边三角形的三条边都相等,三个角都相等。
【解答】解:红领巾的两腰相等,并且有一个角是钝角,因此红领巾如果按角分它是一个钝角三角形,按边分它又是一个等腰三角形。
故答案为:钝角,等腰。
【点评】熟练掌握三角形的分类标准是解答此题的关键。
10.(2021秋•中江县期末)
从左往右数,长方体排第 5 ,球排第 2 ,正方体排第 1 ;正方体有 1 个,圆柱有 3 个;请把右边的3个图形圈起来。
【分析】根据立体图形的识别和分类即可解答。
【解答】解:
从左往右数,长方体排第5,球排第2,正方体排第1;正方体有1个,圆柱有3个;请把右边的3个图形圈起来。
故答案为:5;2;1;1;3。
【点评】本题主要考查立体图形的分类及识别,熟练掌握正方体、长方体、球体的特征是解答本题的关键。
三.判断题(共5小题)
11.(2021秋•黄陂区期末)长方形和正方形可以看成是特殊的平行四边形。 √
【分析】长方形的特征:4条边,相对的两条边相等,4个角,每个角都是直角;正方形的特征:4条边,4条边都相等,4个角,每个角都是直角;而平行四边形的特征是两组对边分别平行且相等的四边形;据此可知长方形、正方形是特殊的平行四边形;由此解答即可。
【解答】解:长方形和正方形可以看成是特殊的平行四边形,说法正确。
故答案为:√。
【点评】根据三种图形的特征,从而得出长方形、正方形是特殊的平行四边形。
12.(2022春•上蔡县月考)长方形、圆、正方体、圆柱都是立体图形。 ×
【分析】有些几何图形(如线段、角、三角形、长方形、圆等)的各个部分都在同一平面内,它们是平面图形;从实物中抽象出来的各种图形,统称为几何图形,几何图形是数学研究的主要对象之一.有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各个部分不都在同一平面内,它们是立体图形,据此解答。
【解答】解:长方形和圆是平面图形,正方体、圆柱都是立体图形。原题说法错误。
故答案为:×。
【点评】本题考查了平面图形和立体图形的区别。
13.(2022•蓝田县模拟)三根分别长8厘米,12厘米,20厘米的小棒可以围成一个三角形。 × 。
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:8+12=20,不符合三角形的三边关系,所以三根分别长8厘米,12厘米,20厘米的小棒不可以围成一个三角形。原题说法错误。
故答案为:×。
【点评】本题考查了三角形的三边关系的应用。
14.(2021秋•丰都县期末)如图信封中装的一定是三角形。 ×
【分析】三角形是由三条线段首尾相接连成的图形,四边形是四条线段围成的图形,有四条边,四个角,通过观察,露出一个角可能是三角形,也可能是四边形或其他的多边形。
【解答】解:通过观察,露出一个角可能是三角形,也可能是四边形或其他的多边形。
故答案为:×。
【点评】本题考查了三角形和多边形的特征知识,结合题意分析解答即可。
15.(2022秋•荣成市期中)把一个三角形的59°的角剪下来,剩下的图形的内角和一定是121°。 ×
【分析】一个三角形剪去一个59°的角,剩下的图形可能是三角形,也可能是四边形,根据三角形的内角和等于180°,四边形的内角和等于360°,解答此题即可。
【解答】解:一个三角形剪去一个59°的角,剩下图形可能是三角形,三角形内角和是180度,剩下图形也可能是四边形,四边形内角和是360度。
所以原题的说法是错误的。
故答案为:×。
【点评】本题考查图形的变化,可拿一张纸按题意剪一个三角形,用折线的方法得出答案。
四.操作题(共1小题)
16.(2022秋•临湘市期中)数一数,填一填。
(1)
4 个, 3 个, 5 个, 2 个。
(2)有 7 个,有 6 个
【分析】根据立体图形的分类和识别知识,分别数出各种立体图形的个数,解答即可。
【解答】解:(1)4 个,3个,5个,2个。
(2)有7个,有6个。
故答案为:4,3,5,2;7,6。
【点评】本题考查了立体图形的认识,分别数出各种立体图形的个数,解答即可。
五.应用题(共4小题)
17.(2019秋•龙岩期末)用木条做成一个长方形框,如果把它拉成一个平行四边形,发生了怎样的变化?请判断并说明理由。
【分析】平面图形的周长就是围成它的所有线段的长度和;将长方形拉成平行四边形后,每个边的长度没变,所以它的周长就不变,但是它的高变小了,因此面积就变小了。据此解答即可。
【解答】解:用木条做成一个长方形框,如果把它拉成一个平行四边形,周长不变,面积变小了。理由:长方形的面积等于长乘宽,长方形拉成四边形,长和底相等,但是平行四边形的高比长方形的宽短。
【点评】此题考查的目的是理解掌握长方形、平行四边形的周长、面积的意义及应用。
18.(2022春•黄梅县期末)有块直角三角形的菜地,已知一个锐角是另一个锐角的4倍,求这两个锐角的度数。
【分析】因为直角三角形中的两个锐角的度数之和是90度,如果一个锐角是另一个锐角的4倍,则把这个锐角看做1份,则另一个锐角就是4份,则它们的和就是1+4=5份,据此求出一份是多少即可解答问题。
【解答】解:90°÷(1+4)
=90°÷5
=18°
18°×4=72°
答:这两个锐角分别是18度和72度。
【点评】此题考查了和倍公式的灵活应用,关键是明确直角三角形的两个锐角的和是90度。
19.(2022春•万州区期末)一块等腰三角形的菜地,已知两条边分别长是79米和39米,如果在它的周围用篱笆围一圈,至少要用篱笆多少米?
【分析】根据任意两边之和大于第三边,可知等腰三角形的腰的长度是79米,底边长39米,据此解答即可。
【解答】解:因为39+39=78(米)
78<79
所以等腰三角形的腰的长度是79米,底边长39米。
周长是:79+79+39=197(米)
答:至少要用篱笆197米。
【点评】关键是先判断出三角形的两条腰的长度,问题即可得解。
20.(2022•海沧区)一个三角形中最小的角是44°,这个三角形可能是哪类三角形?请说明理由。
【分析】三角形的内角和是180°,因为三角形中最小的角是44°,假设第二小的角也是44°,所以最大的角最大为:180°﹣44°﹣44°=92°;假设第二小的角也是46°,所以最大的角最大为:180°﹣44°﹣46°=90°;假设第二小的角是89°,所以第三个角为:180°﹣44°﹣89°=47°,进而判断即可。
【解答】解:假设第二小的角也是44°,所以最大的角最大为:180°﹣44°﹣44°=92°;假设第二小的角也是46°,所以最大的角最大为:180°﹣44°﹣46°=90°;假设第二小的角是89°,所以第三个角为:180°﹣44°﹣89°=47°,所以这个三角形可能是钝角三角形,可能是直角三角形,也可能是锐角三角形。
【点评】解答此题的关键:先进行假设,进而根据三角形的内角和是180°,求出最大的角的度数,进而根据三角形的分类进行解答。
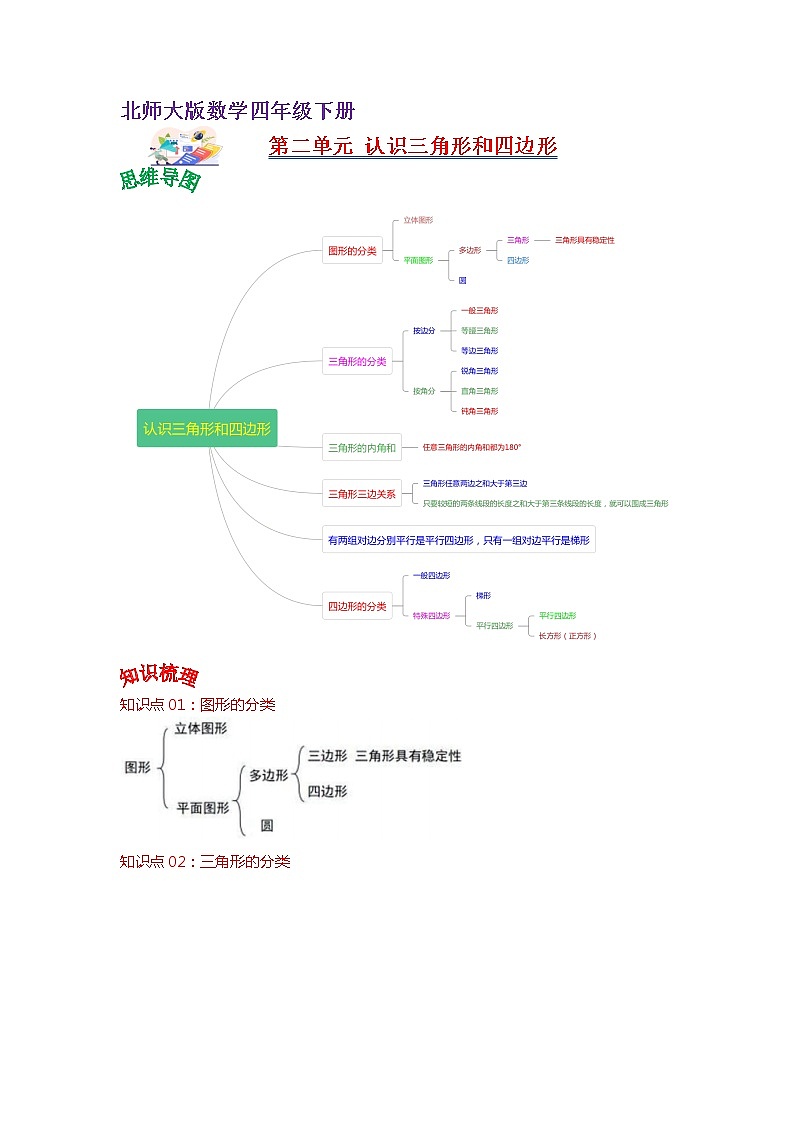
北师大版数学四年级下册
第二单元 认识三角形和四边形
知识点01:图形的分类
知识点02:三角形的分类
等边三角形是特殊的等腰三角形。
知识点03:三角形内角和
任意三角形的内角和都是 180°。
知识点04:三角形三边关系
1. 三角形任意两边之和大于第三边;
2. 判断三条线段能否围成三角形,只要较短的两条线段的长度之和大于第三条线段的长度,就可以围成三角形。
知识点05:平行四边形和梯形
有两组对边分别平行的四边形是平行四边形,只有一组对边平行的四边形是梯形。
知识点06:四边形的分类
考点01:图形的分类
【典例分析01】
1 个
6 个
7 个
10 个
中有 5 个长方形。中有 6 个三角形。
【分析】长方形和正方形都有四条边,四个角都是直角,正方形四条边相等,圆形是一条曲线围成的,三角形是由三条边、三个角组成,平行四边形的对边平行且相等,据此解答。
【解答】解:
1个
6个
7个
10个
中有5个长方形。中有6个三角形。
故答案为:1,6,7,10,5,6。
【点评】本题考查了长方形、正方形、圆形及三角形的特征。
【变式训练01】
2 个
3 个
3 个
4 个
【分析】正方体:有8个顶点,6个面,每个面面积相等(或每个面都有正方形组成);长方体:有8个顶点,6个面,每个面都由长方形或相对的一组正方形组成;圆柱:上下两个面为大小相同的圆形,有一个曲面叫侧面;球:球是生活中最常见的图形之一,例如篮球、足球都是球,球是由一个面所围成的几何体。
【解答】解:
2个
3个
3个
4个
故答案为:2,3,3,4。
【点评】本题考查了长方体、正方体、圆柱及球的特征及认识。
【变式训练02】把各种图形的序号填在横线里。
长方形 ①④
正方形 ③
三角形 ②⑥
圆 ⑤
【分析】根据长方形、正方形、三角形和圆的特征进行分类识别。
【解答】解:把各种图形的序号填在横线里。
长方形 ①④
正方形 ③
三角形 ②⑥
圆 ⑤
故答案为:①④,③,②⑥,⑤。
【点评】本题考查了长方形、正方形、三角形和圆的特征,从而进行分类识别。
【变式训练03】(1)正方体有 2 个;长方体有 4 个;球有 2 个;圆柱有 5 个。
(2) 正方体 的右边是;的 下 面和 左 边是长方体。
(3)有一个图形,它的上面、右边都是圆柱,左边是长方体,这个图形可能是(),也可能是()(把正确的圈起来)。
【分析】根据立体图形的分类及识别方法、常见立体几何图形及性质,找出各种图形并填数。
【解答】解:(1)正方体有2个;长方体有4个;球有2个;圆柱有5个。
(2)正方体的右边是;的下面和左边是长方体。
(3)有一个图形,它的上面、右边都是圆柱,左边是长方体,这个图形可能是(),也可能是()。
故答案为:(1)2,4,2,5;(2)正方体,下,左;(3),。
【点评】此题考查了学生对立体图形的分类及识别的掌握情况。
考点02:三角形的分类、内角和及三边关系
【典例分析02】猜猜下面各是什么三角形。
【分析】任意三角形的内角和都是180度,利用180度减去已知的两个角的度数求出第三个角,根据第三角的特征判断三角形的种类;锐角三角形:最大角小于90°,直角三角形:最大角等于90°,钝角三角形:最大角大于90°;三条边相等的是等边三角形;直角三角形其余两个锐角的和等于直角。
【解答】解:180°﹣28°×2
=180°﹣56°
=124°,三角形最大的角是钝角,这是一个钝角三角形;
180°﹣36°﹣74°
=144°﹣74°
=70°
三角形的3个角都是锐角,因此三角形是锐角三角形。
如图:
【点评】本题考查了三角形按角、按边分类的方法。
【变式训练01】求下列三角形的度数。
【分析】三角形的内角和是180°,(1)(2)用180°减去2个已知角的度数就是第三个角的度数;(3)直角三角形中两个锐角的和是90度,利用90度减去已知的锐角就是另一个角的度数。
据此可解答。
【解答】解:(1)180°﹣55°+85°
=125°﹣85°
=40°
(2)180°﹣30°+35°)
=150°﹣35°
=115°
(3)90°﹣40°=50°
【点评】本题考查了学生对等腰三角形的特征及三角形内角和是180°的知识的掌握情况。
【变式训练02】星期天,明明从家出发到超市,走哪条路最近?最近的路与最远的路相差多远?
【分析】根据两点之间,线段最短,解答此题即可。
【解答】解:1100+1200﹣1300
=2300﹣1300
=1000(米)
答:明明从家出发到超市,走中间路最近,最近的路与最远的路相差1000米。
【点评】熟练掌握两点之间,线段最短,是解答此题的关键。
【变式训练03】请把下面这根纸条裁成3段围成一个三角形。先画一画,再标一标。每段的长度分别是 9 cm、 8 cm、 3 cm。
【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可。
【解答】解:由题意,符合题意的三角形各边可以为:9厘米、8厘米、3厘米。
故答案为:9,8,3。(答案不唯一)。
【点评】围成三角形中任意两条边的和大于第三边,即最长边要小于总长度的一半,是判断三条线段能否围成一个三角形的关键。
考点03:四边形的分类
【典例分析03】选择下面的小棒(每根不能折断),摆出长方形和正方形。
(1)选择 4 根 2 厘米的小棒就能摆出一个正方形。
(2)选择 2 根 3 厘米和 2 根 1 厘米的小棒,就能摆出一个长方形,请把这个长方形画在下面的方格纸上。(下面方格纸中每个小正方形的边长表示1厘米)
【分析】(1)有一组邻边相等且一个角是直角的平行四边形叫做正方形,正方形四条边相等;
(2)长方形的4个内角都是直角,长方形对边相等,据此选择画图。
【解答】解:(1)选择4根2厘米的小棒就能摆出一个正方形。
(2)选择2根3厘米和2根1厘米的小棒,就能摆出一个长方形。
如图:
故答案为:4,2;2,3;2,1。
【点评】本题考查了正方形和长方形的特征及画法。
【变式训练01】按顺序(A→B→C→D→A)连接各点,画出围成
的图形,围成的图形是 平行四边形 。
【分析】先按要求画图,然后进行判断即可。
【解答】解:按顺序(A→B→C→D→A)连接各点,画出围成的图形,围成的图形是平行四边形。
故答案为:平行四边形。
【点评】此题考查了平行四边形的特征。
【变式训练02】填一填。
【分析】根据长方形的特征,长方形有4条边,相对的边长度相等;据此解答即可。
【解答】解:
【点评】此题考查的目的是理解掌握长方形的特征及应用。
【变式训练03】根据图形之间的关系把“①四边形、②平行四边形、③长方形、④正方形、⑤梯形”这几个图形的序号填在下面对应的集合图中.
【分析】根据平行四边形、梯形、长方形和正方形的含义:两组对边都平行的四边形是平行四边形;一组对边平行而另一组对边不平行的四边形是梯形;有一个角是直角的平行四边形是长方形,一组邻边相等的长方形是正方形;可知:正方形是特殊的长方形,长方形是特殊的平行四边形;梯形和平行四边形都是四边形;据此解答即可。
【解答】解:如图所示:
【点评】本题考查的是正方形、平行四边形、梯形和长方形的定义,熟练掌握这些四边形的定义与性质是解答此题的关键。
一.选择题(共6小题)
1.如图三角形中,是直角三角形的是( )
A. B.
C.
【分析】分别计算出各个选项中另一个角的度数,再根据直角三角形的特征判断即可。
【解答】解:A.180°﹣40°﹣30°=110°,110°>90°,是钝角三角形,不符合题意;
B.180°﹣60°﹣30°=90°,90°=90°,是直角三角形,符合题意;
C.180°﹣40°﹣70°=70°,70°<90°,是锐角三角形,不符合题意。
故选:B。
【点评】本题考查了直角三角形的特征。
2.教室黑板的表面是( )。
A.圆形 B.长方形 C.三角形
【分析】根据长方形的特征选择即可。
【解答】解:教室黑板的表面是长方形。
故选:B。
【点评】本题主要考查了平面图形的分类及识别,解题的关键是掌握长方形的特征。
3.下图中不是同类的是( )
A. B. C. D.
【分析】文具盒、笔、墨水属于学习用品,帽子属于生活用品。据此做题。
【解答】解:文具盒、笔、墨水属于学习用品,帽子属于生活用品。
故选:A。
【点评】本题主要考查物体的分类,关键是利用生活常识做题。
4.将两个完全一样的直角三角形拼成一个大三角形,这个大三角形的内角和是( )
A.90° B.180° C.270° D.360°
【分析】只要是三角形,它的内角和就是180度,不管三角形是大还是小,它的内角和都是180度,据此解答.
【解答】解:根据三角形内角和定理,将两个完全一样的直角三角形拼成一个大三角形,这个大三角形的内角和是180°.
故选:B.
【点评】解答此题的主要依据是:三角形的内角和是180度.
5.下列三组线段,可以围成三角形的是( )
A. B.
C.
【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可。
【解答】解:A.5+5=10,所以不能够围成一个三角形;
B.4+5<10,所以不能围成三角形;
C.6+7=13,所以能围成三角形。
故选:C。
【点评】解决此题的关键是根据三角形的特性进行分析、解答。
6.课堂上,老师让每人准备两根长5厘米,两根长7厘米的小棒,然后拼成一个平行四边形。妙妙说:“我们组拼成了形状各异的平行四边形。”丁丁同意妙妙的意见。原因是( )
A.平行四边形容易变形
B.平行四边形的两组对边相等
C.平行四边形的两组对边平行
【分析】根据平行四边形不具有稳定性,解答此题即可。
【解答】解:拼成了形状各异的平行四边形,是因为平行四边形容易变形。
故选:A。
【点评】熟练掌握四边形的特性,是解答此题的关键。
二.填空题(共6小题)
7.我们的红领巾的形状是 三角 形,数学书的封面是 长方 形。
【分析】根据三角形及长方形的特征判断即可。
【解答】解:我们的红领巾的形状是三角形,数学书的封面是长方形。
故答案为:三角,长方。
【点评】本题主要考查了平面图形的分类与识别,解题的关键是熟记三角形及长方形的特征。
8.正方形和长方形都是由 4 条线段围成的图形,它们都有 4 个直角。
【分析】长方形是一种平面图形,长方形的四个角都是直角,同时长方形的对边互相平行且相等;
正方形是有一组邻边相等且一个角是直角的平行四边形。
【解答】解:正方形和长方形都是由4条线段围成的图形,它们都有4个直角。
故答案为:4,4。
【点评】此题考查了正方形和长方形的定义,要熟练掌握。
9.在长是10cm,宽是8cm的长方形里截一个最大的正方形,正方形的边长是 8 cm。
【分析】在长是10cm,宽是8cm的长方形里截一个最大的正方形,正方形的边长就等于长方形的宽,据此解答即可。
【解答】解:在长是10cm,宽是8cm的长方形里截一个最大的正方形,正方形的边长是8cm。
故答案为:8。
【点评】知道正方形的边长就等于长方形的宽,是解答此题的关键。
10.爷爷要用一根长1米的竹条扎一个等腰三角形的风筝骨架,风筝骨架三条边长可能是 3 dm、 3 dm和 4 dm。【长度保留整分米数】
【分析】在同一三角形中,有两条边相等的三角形是等腰三角形,已知要用一根长1米的竹条扎一个等腰三角形的风筝骨架,根据三角形的三边关系,任意两边的和必须大于第三边,但前提是必须有两条边相同,并且三角形三边的和是1米。
【解答】解:1m=10dm
3+3>4,且3+3+4=10;
所以风筝骨架三条边长可能是3dm、3dm和4dm。
故答案为:3,3,4(答案不唯一)。
【点评】本题考查了等腰三角形的特点和三角形的三边关系。
11.一个直角三角形,其中锐角是40°,另一个锐角是 50 °。
【分析】三角形的内角和等于180°,直角三角形有一个角等于90°,180°减去90°,再减去40°,即等于另一个锐角的度数。
【解答】解:180°﹣90°﹣40°
=90°﹣40°
=50°
答:另一个锐角是50°。
故答案为:50。
【点评】熟练掌握三角形内角和知识是解答本题的关键。
12.在按角为三角形分类时,如果只凭其中一个角就可以确定这个三角形的类型,那么它不可能是 锐 角三角形。
【分析】锐角三角形:三个角都小于90°;直角三角形:可记作Rt△.其中一个角必须等于90°;钝角三角形:有一个角大于90°,据此解答。
【解答】解:在按角为三角形分类时,如果只凭其中一个角就可以确定这个三角形的类型,那么它不可能是锐角三角形。
故答案为:锐。
【点评】本题考查了三角形按角分类的方法。
三.判断题(共5小题)
13.在一个三角形里最多有一个直角,至少有一个锐角。 ×
【分析】根据三角形的内角和等于180°,解答此题即可。
【解答】解:在一个三角形里最多有一个直角,至少有两个锐角。
所以题干说法是错误的。
故答案为:×。
【点评】熟练掌握三角形的内角和知识,是解答此题的关键。
14.一个梯形上底与下底间的距离处处相等. √ .
【分析】因为梯形的上下底是平行的,所以夹在两平行线之间的距离是处处相等,据此可知:梯形上底与下底间的距离处处相等的说法是正确的.
【解答】解:梯形上底与下底间的距离就是这个梯形的高,所以处处相等的说法是正确的.
故判断为:√.
【点评】此题考查梯形的特征,即上下底平行,还要明确夹在两平行线之间的距离是处处相等的.
15.是可以滚动的。 √
【分析】根据圆柱体的特征进行判断即可。
【解答】解:圆柱体是可以滚动的,原题说法正确。
故答案为:√。
【点评】本题考查圆柱体的特征。
16.一个三角形中有2个锐角,则这个三角形一定是锐角三角形。 ×
【分析】直角三角形有一个直角和2个锐角;钝角三角形有一个钝角和2个锐角,锐角三角形必须有3个锐角,据此解答。
【解答】解:一个三角形中有2个锐角,则这个三角形可能是锐角三角形,也可能是直角三角形或钝角三角形,原题说法错误。
故答案为:×。
【点评】本题考查了三角形的分类。
17.用分别长4cm、3cm、7cm的小棒可以围成一个三角形。 ×
【分析】求出较短两条边的和,与第三条边比较,比第三条边长就可以,否则构不成三角形
【解答】解:3+3=6(厘米)
6<7,构不成三角形,故原题错误。
故答案为:×。×
【点评】本题根据三角形任意两边之和大于第三边进行判断。
四.操作题(共1小题)
18.你能把各种图形整理一下吗?
图形
□
〇
△
个数
(1)一共有 22 个图形,最多的是 圆形 , 正方形 和 三角形 同样多。
(2)比□多 6 个,比〇少 2 个。
【分析】(1)根据长方形、正方形、三角形、圆的特征进行分类识别,数出相应的数量通过计算得出共有图形的个数,然后通过比较不同图形的数量解答;
(2)根据图形数量列式计算解答。
【解答】解:
图形
□
〇
△
个数
8
2
10
2
(1)一共有图形:8+2+10+2=22(个),最多的是圆形,正方形和三角形同样多。
(2)比□多:8﹣2=6(个),比〇少10﹣8=2(个)。
故答案为:22,圆形,正方形,三角形;6,2。
【点评】本题考查了长方形、正方形、三角形、圆的特征,从而进行分类识别。
五.应用题(共4小题)
19.猪八戒走一步的长度是8分米,有一间房子,房子的长是八戒走了10步的长度,宽是八戒走了5步的长度,你能知道这间房子的长和宽各是多少米吗?
【分析】用每步的长度乘步数,求出房子的长和宽,据此解答。
【解答】解:长:8×10=80(分米)
80分米=8米
宽:8×5=40(分米)
40分米=4米
答:这间房子的长大约是8米,宽大约是4米。
【点评】本题主要考查了整数乘法运用的理解和灵活运用情况。
20.用一根217厘米长的铁丝正好围成一个等腰梯形。梯形的上底是31厘米,下底是66厘米,它的一条腰长多少厘米?
【分析】等腰梯形的两腰相等,用一根217厘米长的铁丝正好围成一个等腰梯形,铁丝的总长减去上下底的长就是两腰的长,再除以2即可。
【解答】解:(217﹣31﹣66)÷2
=120÷2
=60(厘米)
答:它的一条腰长60厘米。
【点评】本题考查了等腰梯形的特征。
21.王老师准备了12厘米和6厘米的木棒各一根,现在他想拼成一个三角形,这个三角形第三边最长是多少厘米?最短是多少厘米?(取整厘米)
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:12+6=18(厘米)
12﹣6=6(厘米)
根据三角形的三边关系,因此三角形的第三边必须在6和118之间,因此最长是:18﹣1=17(厘米),最短是6+1=7(厘米)。
答:这个三角形第三边最长是17厘米,最短是7厘米。
【点评】本题考查了三角形的三边关系的应用。
22.王明做了一个等腰三角形风筝,它的顶角是76°,它的一个底角是多少度?
【分析】根据等腰三角形的两底角相等,和三角形的内角和等于180°,解答此题即可。
【解答】解:(180﹣76)÷2
=104÷2
=52(度)
答:它的一个底角是52度。
【点评】熟练掌握三角形的内角和知识和等腰三角形的性质,是解答此题的关键。
一.选择题(共5小题)
1.能向任意方向滚动的是( )
A. B.
C.
【分析】根据立体图形的分类及特征即可解答。
【解答】解:能向任意方向滚动的是球。
故选:C。
【点评】本题主要考查立体图形的特征等。
2.一个三角形最小的锐角是50度,这个三角形一定是( )三角形.
A.钝角 B.直角 C.锐角
【分析】由三角形的内角和求出另外两个角的和,再根据最小的内角是50°来判断其它两个角的情况.
【解答】解:180°﹣50°=130°;
另外两个角的和是130°,最小的内角是50°,
假设另外两个角中还有一个是50°,另一个就是:130°﹣50°=80°;
最大的内角最大只能是80°,所以这个三角形的三个角都是锐角,这个三角形一定是锐角三角形.
故选:C.
【点评】解决本题首先要能根据三角形的内角和是180°,求出另外角的度数可能的情况,并由此求解.
3.一个等腰三角形中,其中一底角是75度,顶角是( )
A.75度 B.45度 C.30度
【分析】因为等腰三角形的两个底角相等,其中一底角是75度,另一个底角也是75°,根据三角形的内角和是180°,所以用180°减去两个底角的度数就是顶角的度数。
【解答】解;180°﹣75°×2
=180°﹣150°
=30°
答:顶角是30°。
故选:C。
【点评】本题要根据等腰三角形的两个底角相等和三角形的内角和是180°这两个知识点解答。
4.璐璐用小棒围三角形,已经选了长5厘米和8厘米的各一根,第三根应该选( )厘米的小棒。
A.14 B.7 C.3 D.2
【分析】根据三角形的两边之和大于第三边,两边之差小于第三边,解答此题即可。
【解答】解:8﹣5<第三边<8+5
3<第三边<13
答:第三根小棒的长度最长不能超过12厘米,最短不少于4厘米,所以第三根应该选7厘米的小棒。
故选:B。
【点评】熟练掌握三角形的三边关系,是解答此题的关键。
5.图的长方形由铁丝围成,在a、b、c、d拐弯处做上记号“•”,再从其中一个拐弯点把铁丝剪开拉直,那么铁丝可能是( )
A. B.
C. D.
【分析】根据长方形的特征:由4条边围成,对边平行且相等,因为长方形两条长,两条宽,所以长方形拉直后,这根铁丝应该是分成长、宽、长、宽四段;由此结合选项进行选择即可。
【解答】解:如图的长方形由铁丝围成,在a、b、c、d拐弯处做上记号“•”,再从其中一个拐弯点把铁丝剪开拉直,那么铁丝可能是。
故选:C。
【点评】灵活掌握长方形的特征,是解答此题的关键。
二.填空题(共5小题)
6.
上面10个图形中,四边形有 6 个, 1 是正方形, 4、8 是长方形。
【分析】有4条边首尾相连的图形是四边形,最后找出正方形和长方形即可,据此解答。
【解答】解:上面10个图形中,四边形有6个,1是正方形,4、8是长方形。
故答案为:6,1,4、8。
【点评】本题考查了四边形的特征及分类,结合题意分析解答即可。
7.现有两根分别长3厘米和5厘米的小棒,如果再添一根小棒围成一个三角形。那么这根小棒最短应该是 3 厘米,最长是 7 厘米。(取整厘米数)
【分析】三角形的三条边中,任意两边之和大于第三边,任意两边之差小于第三边,由此解答即可。
【解答】解:三根小棒首尾相连围成一个三角形,已知其中两根小棒分别长3厘米和5厘米,因此它的第三边最长是3+5﹣1=7(厘米),最短是5﹣3+1=3(厘米)
答:小棒最短可能是3厘米,最长可能是7厘米。
故答案为:3;7。
【点评】本题考查了三角形的三边关系的应用。
8.一个等腰三角形的底角是45度,它的顶角是 90 度,这还是一个 直 角三角形:根据三角形的内角和可以推算出梯形内角和是 360 度。
【分析】根据等腰三角形的特征,等腰三角形的两个底角相等,三角形的内角和是180度,用三角形的内角和减去两个底角的度数就是顶角的度数。梯形可以分成两个三角形,所以梯形的内角和是360度。据此解答。
【解答】解:180°﹣45°﹣45°=90°
180°×2=360°
答:它的顶角是90°,还是一个直角三角形,梯形的内角和是360°。
故答案为:90,直,360。
【点评】此题考查的目的是理解等腰直角三角形的特征及应用,三角形的内角和及应用。
9.已知一个三角形的一个锐角是50°,另一个锐角是70°,第三个角是 60° 。这是一个 锐角 三角形。
【分析】三角形的内角和是180度,用180度减去已知的两个角的和就是第三个角的度数,进而根据最大角的度数判断三角形的类别。
【解答】解:180°﹣(50°+70°)
=180°﹣120°
=60°
最大角是70°,是锐角,所以这是一个锐角三角形。
答:第三个角是60°,这是一个锐角三角形。
故答案为:60°,锐角。
【点评】此题主要考查三角形的内角和是180度的灵活运用以及三角形的分类。
10.数一数。
2
6
5
2
2
【分析】长方形和正方形都有四条边,四个角都是直角,正方形四条边相等,圆形是一条曲线围成的,三角形是由三条边、三个角组成,平行四边形的对边平行且相等,据此解答。
【解答】解:如表:
2
6
5
2
2
故答案为:2,6,5,2,2。
【点评】本题考查了长方形、正方形、三角形、圆形及平行四边形的特征及认识。
三.判断题(共5小题)
11.羽毛球的形状是球。 ×
【分析】球是生活中最常见的图形之一,例如篮球、足球都是球,羽毛球的形状不是球,由此解答即可。
【解答】解:羽毛球的形状不是球,原题说法错误。
故答案为:×。
【点评】本题考查了球的特征。
12.在一个三角形的三个角中,如果只有两个角是锐角,那么这个三角形一定不是直角三角形。 ×
【分析】根据三角形的内角和是180°可知,如果一个三角形只有两个内角是锐角,则另外一个角可以是直角或钝角,则这个三角形可能是直角三角形,也可能是钝角三角形;解答即可。
【解答】解:由三角形的内角和是180°可知,如果一个三角形只有两个内角是锐角,则另外一个角可以是直角,也可以是钝角,
则这个三角形一定是直角或钝角三角形。所以原题说法错误。
故答案为:×。
【点评】此题主要考查三角形的内角和及三角形的分类。
13.一个三角形最少有两个锐角,最多有三个锐角. √ .
【分析】根据三角形的内角和等于180°,三个角中最多有一个直角或钝角,所以最少有两个锐角;而如果一个三角形中没有直角或钝角,则三个角就都是锐角,即最多有3个锐角,据此即可判断.
【解答】解:因为三角形的内角和等于180°,
所以三角形最多有一个直角或钝角,剩下的两个为锐角;
所以一个三角形中,最少有2个锐角;
如果一个三角形中没有直角或钝角,则三个角就都是锐角,
因此最多有3个锐角;
所以“一个三角形最少有两个锐角,最多有三个锐角”的是说法是正确的.
故答案为:√.
【点评】此题考查了三角形内角和定理的灵活应用.
14.从2厘米、3厘米、4厘米、6厘米的4根小棒中选三根围成一个三角形,有2种不同的选法。 √
【分析】根据三角形三条边之间的关系,在三角形中,任意两边之和大于第三边,任意两边之差小于第三边。据此解答即可。
【解答】解:因为2+3=5(厘米)
5厘米大于4厘米
所以用2厘米、3厘米、4厘米三根小棒可以围成一个三角形;
因为3+4=7(厘米)
7厘米大于6厘米
所以用3厘米、4厘米、6厘米三根小棒可以围成一个三角形;
因此,从2厘米、3厘米、4厘米、6厘米的4根小棒中选三根围成一个三角形,有2种不同的选法。
故答案为:√。
【点评】此题考查的目的是理解掌握三角形三条边之间的关系及应用。
15.正方形是特殊的长方形,长方形是特殊的平行四边形. √ .
【分析】根据平行四边形的意义,对边平行的四边形是平行四边形,长方形对边也平行,因此它属于平行四边形,即角为直角的特殊平行四边形;根据长方形的意义,两组对边平行,角为直角,根据正方形两组对边平行且相等,角为直角,即正方形是四条边都相等的特殊长方形.即正方形是特殊的长方形,长方形是特殊的平行四边形.
【解答】解:如图
正方形是四条边相等的特殊长方形
长方形是角为直角的特殊平行四边形
因此,正方形是特殊的长方形,长方形是特殊的平行四边形,这种说法正确.
故答案为:√.
【点评】根据平行四边形、长方形、正方形的意义或特征即可判定.
四.操作题(共3小题)
16.(1)请在下方右边空白处画一个与如图完全一样的直角梯形。
(2)在原图中画出:上底延长到E,连接EC后变成一个长方形。再想象填一填:如果把画好后的长方形AB边向上延长1厘米到F,并连接EF,又会变成 梯 形。
【分析】(1)根据要求,结合梯形的画法,画一个与如图完全一样的直角梯形即可。
(2)根据要求,上底延长到E,连接EC后变成一个长方形。
再想象填一填:如果把画好后的长方形AB边向上延长1厘米到F,并连接EF,又会变成梯形。
【解答】解:作图如下:
如果把画好后的长方形AB边向上延长1厘米到F,并连接EF,又会变成梯形。
故答案为:梯。
【点评】本题考查了梯形的特征及画法知识,结合题意分析解答即可。
17.在能拼成三角形的小棒下面画“☆”.(单位:厘米)
【分析】根据三角形的三边关系:三角形任意两边之和大于第三边,对各选项进行逐一分析即可.
【解答】解:A、5+4=9>6,能组成三角形;
B、4+4=8>6,能组成三角形;
C、2+3=5<7,不能组成三角形;
故答案为:
【点评】本题考查的是三角形的三边关系,即三角形任意两边之和大于第三边,任意两边之差小于第三边;实际判断时选取两条较短的边求和再与最大边进行比较即可.
18.在点子图上画一个锐角三角形.
【分析】三个角都是锐角的三角形是锐角三角形,由此画出即可.
【解答】解:
【点评】明确锐角三角形的含义,是解答此题的关键.
五.应用题(共2小题)
19.一块平行四边形的菜地,一条边长为8米,比另一条边短2米。围这块菜地需要多长的栅栏?
【分析】平行四边形的两组对边分别相等,据此求出相邻的两条边的和,再乘2即可得出平行四边形的周长,即围这块菜地需要的栅栏长。
【解答】解:(8+8+2)×2
=18×2
=36(米)
答:围这块菜地需要36米长栅栏。
【点评】此题主要考查平行四边形的周长的计算应用。
20.一个等腰三角的一个顶角是64°,它的一个底角是多少度?如果它的底角是64°,那么它的顶角是多少度?
【分析】三角形内角和等于180°,等腰三角形的两个底角相等;180°减顶角的度数,再除以2等于一个底角的度数;180°减两个底角的度数,等于顶角的度数;据此即可解答。
【解答】解:(180°﹣64°)÷2
=116°÷2
=58°
180°﹣64°×2
=180°﹣128°
=52°
答:一个等腰三角的一个顶角是64°,它的一个底角是58°;一个等腰三角底角是64°,它的顶角是52°。
【点评】本题主要考查学生对三角形的内角和及等腰三角形的特征的掌握和灵活运用。
一.选择题(共5小题)
1.(2021秋•黄陂区期末)下面( )搭得最稳。
A. B. C.
【分析】结合图中几何形体的特性,分析哪组搭得最稳。
【解答】解:A组将圆柱放在正方体放上,正方体与桌面、正方体与圆柱体的接触面都是一个平面,所以搭得较为稳当;
B组将长方体放在圆柱体上,圆柱体在桌面上容易沿侧面方向滚动,球也容易从圆柱上滚落下来;
C组将球放在正方体上,球在正方体上容易滚动滑落下来。
故选:A。
【点评】球容易向桌面四周滚动,圆柱容易沿侧面方向在桌面上滚动。
2.(2022秋•密云区期末)如图所示图中能正确表示锐角三角形、直角三角形、钝角三角形之间关系的是( )
A. B.
C.
【分析】三角形按角分,锐角三角形:三个角都小于90°;直角三角形:可记作Rt△.其中一个角必须等于90°;钝角三角形:有一个角大于90°,它们之间是并存的关系。
【解答】解:三角形按角分为锐角三角形、直角三角形和钝角三角形,它们的关系是。
故选:C。
【点评】本题考查了三角形按角分类的方法。
3.(2020春•嘉荫县期末)下列三组度数中,能组成三角形的是( )
A.50°,50°,50° B.60°,60°,60°
C.70°,70°,70°
【分析】根据三角形的内角和是180°,分析解答即可。
【解答】解:A.50°+50°+50°=150°,小于180°,不能组成三角形;
B.60°+60°+60°=180°,符合三角形内角和180°,可以组成三角形;
C.70°+70°+70°=210°,大于180°,不能组成三角形。
故选:B。
【点评】本题考查了三角形内角和知识,结合题意分析解答即可。
4.(2022春•城阳区期末)下面几组小棒,( )组小棒能围成三角形。(单位:cm)
A.7,7,7 B.10,2,12 C.3,5,10
【分析】依据三角形的两边之和大于第三边的特点,即可进行判断。
【解答】解:A、因为7+7>7,所以能围成三角形;
B、因为10+2=12,所以不能围成三角形;
C、因为3+5<10,所以不能围成三角形。
故选:A。
【点评】此题主要考查三角形的两边之和大于第三边的特点。
5.(2022秋•石景山区期末)如图所示图形中是四边形的是( )
A. B. C. D.
【分析】四边形就是四条线段围成的图形,有四条边,四个角,据此选择。
【解答】解:是四边形。
故选:D。
【点评】本题考查了四边形的特征。
二.填空题(共5小题)
6.(2021春•滁州期末)一个梯形上底长4厘米,下底长6厘米,高3厘米(如图)。如果将上底向一端延长2厘米,则变成一个 平行四边 形;如果将上底缩短4厘米,则变成一个 三角 形。
【分析】根据梯形的定义可知:梯形的两个底互相平行且不相等,如果将上底延长2厘米,则上底变成4+2=6厘米,与下底相等了,由此根据一组对边平行且相等的四边形是平行四边形,即可解答;
当上底缩短4厘米时,4﹣4=0,即上底缩为一个点,此时梯形变为三角形。
【解答】解:4+2=6(厘米)
则上底与下底相等,因为平行四边形的对边平行且相等,所以这个图形是平行四边形;
当上底缩短4厘米时,4﹣4=0,
即上底缩为一个点,此时梯形变为三角形。
故答案为:平行四边,三角。
【点评】此题考查了梯形与平行四边形的定义与性质的灵活应用:一组对边平行且相等的四边形是平行四边形,还考查了三角形的特点,结合题意解答即可。
7.(2021秋•新泰市期末)用小棒围成三角形,其中两根小棒分别长7厘米和5厘米,第三根小棒最长 11 厘米,最短 3 厘米,可以围成三角形。(填整厘米数)
【分析】根据三角形的三边关系:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可。
【解答】解:7+5=12(厘米)
最长:12﹣1=11(厘米)
7﹣5=2(厘米)
最短:2+1=3(厘米)
因此第三根小棒最长11厘米,最短3厘米。
故答案为:11,3。
【点评】此题关键是根据三角形的三边关系进行分析、解答。
8.(2022春•梁平区期末)一个三角形,其中两个内角的度数分别是58°、62°,第三个内角是 60 度;1个直角三角形,其中一个锐角是36°,另一个锐角是 54 度。
【分析】根据三角形的内角和等于180°,解答此题即可。
【解答】解:180﹣(58+62)
=180﹣120
=60(度)
180﹣90﹣36
=90﹣36
=54(度)
答:一个三角形,其中两个内角的度数分别是58°、62°,第三个内角是60度;1个直角三角形,其中一个锐角是36°,另一个锐角是54度。
故答案为:60;54。
【点评】熟练掌握三角形的内角和知识,是解答此题的关键。
9.(2022春•鄂伦春自治旗期末)红领巾是我们少先队员佩戴的标志,如果按角分它是一个 钝角 三角形,按边分它又是一个 等腰 三角形。
【分析】根据三角形的分类标准,以及红领巾的特点进行填空即可;三角形按角分为:钝角三角形、直角三角形和锐角三角形,有一个角是钝角的三角形是钝角三角形,有一个角是直角的三角形是直角三角形,三个角都是锐角的三角形是锐角三角形;按边分为:等腰三角形、等边三角形,等腰三角形的两腰相等,两个底角也相等;等边三角形的三条边都相等,三个角都相等。
【解答】解:红领巾的两腰相等,并且有一个角是钝角,因此红领巾如果按角分它是一个钝角三角形,按边分它又是一个等腰三角形。
故答案为:钝角,等腰。
【点评】熟练掌握三角形的分类标准是解答此题的关键。
10.(2021秋•中江县期末)
从左往右数,长方体排第 5 ,球排第 2 ,正方体排第 1 ;正方体有 1 个,圆柱有 3 个;请把右边的3个图形圈起来。
【分析】根据立体图形的识别和分类即可解答。
【解答】解:
从左往右数,长方体排第5,球排第2,正方体排第1;正方体有1个,圆柱有3个;请把右边的3个图形圈起来。
故答案为:5;2;1;1;3。
【点评】本题主要考查立体图形的分类及识别,熟练掌握正方体、长方体、球体的特征是解答本题的关键。
三.判断题(共5小题)
11.(2021秋•黄陂区期末)长方形和正方形可以看成是特殊的平行四边形。 √
【分析】长方形的特征:4条边,相对的两条边相等,4个角,每个角都是直角;正方形的特征:4条边,4条边都相等,4个角,每个角都是直角;而平行四边形的特征是两组对边分别平行且相等的四边形;据此可知长方形、正方形是特殊的平行四边形;由此解答即可。
【解答】解:长方形和正方形可以看成是特殊的平行四边形,说法正确。
故答案为:√。
【点评】根据三种图形的特征,从而得出长方形、正方形是特殊的平行四边形。
12.(2022春•上蔡县月考)长方形、圆、正方体、圆柱都是立体图形。 ×
【分析】有些几何图形(如线段、角、三角形、长方形、圆等)的各个部分都在同一平面内,它们是平面图形;从实物中抽象出来的各种图形,统称为几何图形,几何图形是数学研究的主要对象之一.有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各个部分不都在同一平面内,它们是立体图形,据此解答。
【解答】解:长方形和圆是平面图形,正方体、圆柱都是立体图形。原题说法错误。
故答案为:×。
【点评】本题考查了平面图形和立体图形的区别。
13.(2022•蓝田县模拟)三根分别长8厘米,12厘米,20厘米的小棒可以围成一个三角形。 × 。
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:8+12=20,不符合三角形的三边关系,所以三根分别长8厘米,12厘米,20厘米的小棒不可以围成一个三角形。原题说法错误。
故答案为:×。
【点评】本题考查了三角形的三边关系的应用。
14.(2021秋•丰都县期末)如图信封中装的一定是三角形。 ×
【分析】三角形是由三条线段首尾相接连成的图形,四边形是四条线段围成的图形,有四条边,四个角,通过观察,露出一个角可能是三角形,也可能是四边形或其他的多边形。
【解答】解:通过观察,露出一个角可能是三角形,也可能是四边形或其他的多边形。
故答案为:×。
【点评】本题考查了三角形和多边形的特征知识,结合题意分析解答即可。
15.(2022秋•荣成市期中)把一个三角形的59°的角剪下来,剩下的图形的内角和一定是121°。 ×
【分析】一个三角形剪去一个59°的角,剩下的图形可能是三角形,也可能是四边形,根据三角形的内角和等于180°,四边形的内角和等于360°,解答此题即可。
【解答】解:一个三角形剪去一个59°的角,剩下图形可能是三角形,三角形内角和是180度,剩下图形也可能是四边形,四边形内角和是360度。
所以原题的说法是错误的。
故答案为:×。
【点评】本题考查图形的变化,可拿一张纸按题意剪一个三角形,用折线的方法得出答案。
四.操作题(共1小题)
16.(2022秋•临湘市期中)数一数,填一填。
(1)
4 个, 3 个, 5 个, 2 个。
(2)有 7 个,有 6 个
【分析】根据立体图形的分类和识别知识,分别数出各种立体图形的个数,解答即可。
【解答】解:(1)4 个,3个,5个,2个。
(2)有7个,有6个。
故答案为:4,3,5,2;7,6。
【点评】本题考查了立体图形的认识,分别数出各种立体图形的个数,解答即可。
五.应用题(共4小题)
17.(2019秋•龙岩期末)用木条做成一个长方形框,如果把它拉成一个平行四边形,发生了怎样的变化?请判断并说明理由。
【分析】平面图形的周长就是围成它的所有线段的长度和;将长方形拉成平行四边形后,每个边的长度没变,所以它的周长就不变,但是它的高变小了,因此面积就变小了。据此解答即可。
【解答】解:用木条做成一个长方形框,如果把它拉成一个平行四边形,周长不变,面积变小了。理由:长方形的面积等于长乘宽,长方形拉成四边形,长和底相等,但是平行四边形的高比长方形的宽短。
【点评】此题考查的目的是理解掌握长方形、平行四边形的周长、面积的意义及应用。
18.(2022春•黄梅县期末)有块直角三角形的菜地,已知一个锐角是另一个锐角的4倍,求这两个锐角的度数。
【分析】因为直角三角形中的两个锐角的度数之和是90度,如果一个锐角是另一个锐角的4倍,则把这个锐角看做1份,则另一个锐角就是4份,则它们的和就是1+4=5份,据此求出一份是多少即可解答问题。
【解答】解:90°÷(1+4)
=90°÷5
=18°
18°×4=72°
答:这两个锐角分别是18度和72度。
【点评】此题考查了和倍公式的灵活应用,关键是明确直角三角形的两个锐角的和是90度。
19.(2022春•万州区期末)一块等腰三角形的菜地,已知两条边分别长是79米和39米,如果在它的周围用篱笆围一圈,至少要用篱笆多少米?
【分析】根据任意两边之和大于第三边,可知等腰三角形的腰的长度是79米,底边长39米,据此解答即可。
【解答】解:因为39+39=78(米)
78<79
所以等腰三角形的腰的长度是79米,底边长39米。
周长是:79+79+39=197(米)
答:至少要用篱笆197米。
【点评】关键是先判断出三角形的两条腰的长度,问题即可得解。
20.(2022•海沧区)一个三角形中最小的角是44°,这个三角形可能是哪类三角形?请说明理由。
【分析】三角形的内角和是180°,因为三角形中最小的角是44°,假设第二小的角也是44°,所以最大的角最大为:180°﹣44°﹣44°=92°;假设第二小的角也是46°,所以最大的角最大为:180°﹣44°﹣46°=90°;假设第二小的角是89°,所以第三个角为:180°﹣44°﹣89°=47°,进而判断即可。
【解答】解:假设第二小的角也是44°,所以最大的角最大为:180°﹣44°﹣44°=92°;假设第二小的角也是46°,所以最大的角最大为:180°﹣44°﹣46°=90°;假设第二小的角是89°,所以第三个角为:180°﹣44°﹣89°=47°,所以这个三角形可能是钝角三角形,可能是直角三角形,也可能是锐角三角形。
【点评】解答此题的关键:先进行假设,进而根据三角形的内角和是180°,求出最大的角的度数,进而根据三角形的分类进行解答。

相关资料
更多









