小学数学苏教版三年级下册六 长方形和正方形的面积课时训练

这是一份小学数学苏教版三年级下册六 长方形和正方形的面积课时训练，文件包含第六单元长方形和正方形的面积教师版2022-2023学年三年级下册数学苏教版知识点总结+练习学案docx、第六单元长方形和正方形的面积学生版2022-2023学年三年级下册数学苏教版知识点总结+练习学案docx等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。

苏教版数学三年级下册

第六单元 长方形和正方形的面积




知识点01：认识面积
1. 面积的意义: 物体的表面或平面图形的大小叫作它们的面积。
2. 比较两个物体的表面或平面图形面积大小的方法
(1)观察法；(2)重叠法；(3)同一物体度量法；(4)数方格法
知识点02：认识面积单位
1. 常用的面积单位:平方厘米、平方分米、平方米，用字母(符号)表示分别是cm2、dm2、m2。
2. 认识面积单位:
①平方厘米:边长是1厘米的正方形，面积是1平方厘米；
②平方分米:边长是1分米的正方形，面积是1平方分米；
③平方米:边长是1米的正方形，面积是1平方米。
3. 面积单位间的进率:1平方米=100平方分米，1平方分米=100平方厘米，1平方米=10000平方厘米。
知识点03：计算长方形和正方形的面积
1. 长方形的面积=长×宽，字母公式是S=a×b。
2. 正方形的面积=边长×边长，字母公式是S=a×a。
知识点04：比较两个图形面积大小的方法
当无法用观察法和重叠法比较出两个图形面积的大小时，可以采用数方格法进行比较。无论采用哪种方法，在同一题中标准应统一。

考点01：面积和面积单位

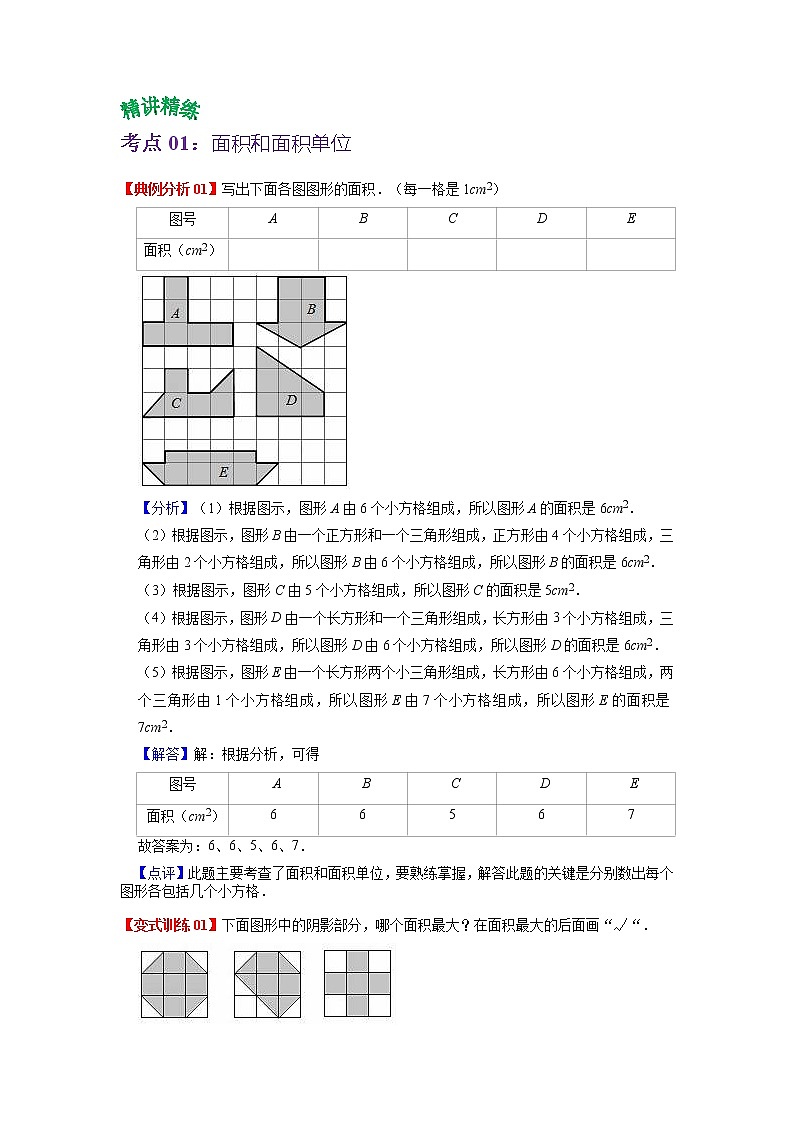
【典例分析01】写出下面各图图形的面积．（每一格是1cm2）
图号
A
B
C
D
E
面积（cm2）






【分析】（1）根据图示，图形A由6个小方格组成，所以图形A的面积是6cm2．
（2）根据图示，图形B由一个正方形和一个三角形组成，正方形由4个小方格组成，三角形由2个小方格组成，所以图形B由6个小方格组成，所以图形B的面积是6cm2．
（3）根据图示，图形C由5个小方格组成，所以图形C的面积是5cm2．
（4）根据图示，图形D由一个长方形和一个三角形组成，长方形由3个小方格组成，三角形由3个小方格组成，所以图形D由6个小方格组成，所以图形D的面积是6cm2．
（5）根据图示，图形E由一个长方形两个小三角形组成，长方形由6个小方格组成，两个三角形由1个小方格组成，所以图形E由7个小方格组成，所以图形E的面积是7cm2．
【解答】解：根据分析，可得
图号
A
B
C
D
E
面积（cm2）
6
6
5
6
7
故答案为：6、6、5、6、7．
【点评】此题主要考查了面积和面积单位，要熟练掌握，解答此题的关键是分别数出每个图形各包括几个小方格．

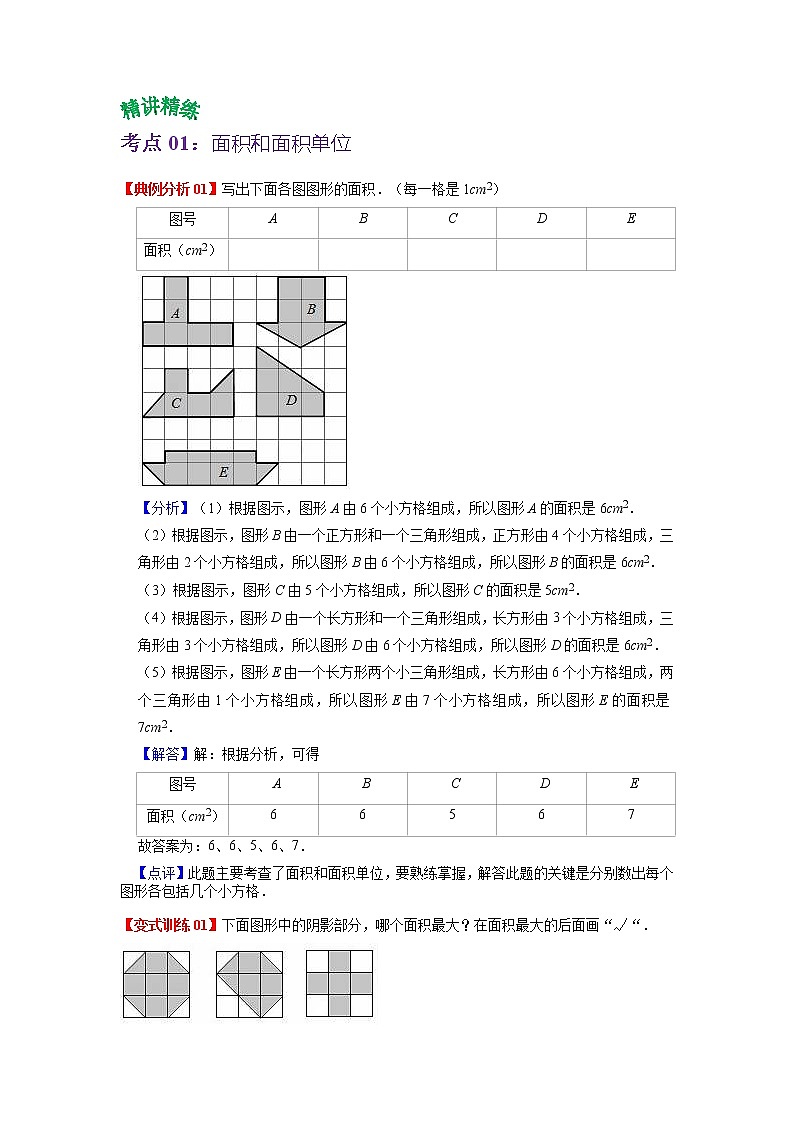
【变式训练01】下面图形中的阴影部分，哪个面积最大？在面积最大的后面画“√“．

【分析】分别数出每个图形中小方格的个数，再比较大小即可．
【解答】解：图①中有7个小方格，
图②中有5.5个小方格，
图③中有5个小方格，
所以图①的面积最大，图③的面积最小．
如图：
【点评】分别数出每个图形中小方格的个数，是解答本题的关键．
【变式训练02】下面的每个小方格都表示1平方厘米．请把每个图形中涂色部分的面积填在括号里．

【分析】①从最下层数起有小方格：1、2、3、4个，加起来即可得解；
②把四个角的为涂色部分四个半方格加起来得2平方厘米，用总数4×4＝16平方厘米减去2平方厘米，即可得解；
③总面积是4×4＝16平方厘米，涂色部分占总面积的，16×＝4平方厘米，即可得解．
【解答】解：①1+2+3+4＝10（平方厘米），
②4×4﹣2＝14（平方厘米），
③4×4×＝4（平方厘米）；

故答案为：10，14，4．
【点评】此题考查了求涂色部分面积的计算方法，在计算时，要灵活地进行图形的转化．
【变式训练03】在〇里填上“＞”“＜”或“＝”．
500平方厘米〇60平方分米
99平方分米〇1平方米
700平方分米〇7平方米
1平方米〇900平方厘米
【分析】（1）500平方厘米＝5平方分米，5平方分米＜60平方分米．
（2）1平方米＝100平方分米，99平方分米＜100平方分米．
（3）低级单位平方分米化高级单位平方米除以进率100，即700平方分米＝7平方米．
（4）1平方米＝10000平方厘米，10000平方厘米＞900平方厘米．
【解答】解：（1）500平方厘米＜60平方分米
（2）99平方分米＜1平方米
（3）700平方分米＝7平方米
（4）1平方米＞900平方厘米．
故答案为：＜，＜，＝，＞．
【点评】不同单位的名数的大小比较通常是先化成相同的单位名数，再根据数值的大小进行比较．
考点02：长方形、正方形的面积

【典例分析02】妈妈用24米长的篱笆围了一块长方形的菜地（如图：一面靠墙），菜地的宽是5米，这块菜地的面积是多少平方米？

【分析】长方形的长等于篱笆的总长减去菜地的宽5米的2倍，就是长方形菜地的长，根据长方形的面积＝长×宽，代入数据解答即可。
【解答】解：24﹣5×2
＝24﹣10
＝14（米）
14×5＝70（平方米）
答：这块菜地的面积是70平方米。
【点评】此题主要考查长方形面积公式的灵活运用，关键是求出长。

【变式训练01】有一个长50m宽30m的长方形菜地。要在一边不动的情况下，把它扩建成一块正方形菜地，面积至少增加多少m2？

【分析】根据正方形的面积＝边长×边长，长方形的面积＝长×宽，把数据代入公式求出扩建后的面积与原来面积的差即可。
【解答】解：50×50﹣50×30
＝2500﹣1500
＝1000（平方米）
答：面积至少增加1000平方米。
【点评】此题主要考查正方形、长方形面积公式的灵活运用，关键是熟记公式。
【变式训练02】一块长方形草坪（如图），长不变，把宽增加16米。扩大后的草坪面积是多少平方米？
【分析】根据长方形的面积＝长×宽，再根据积的变化规律，一个因数不变，另一个因数扩大到原来的几倍，积就扩大到原来的几倍，先求出扩大后的宽是原来的几倍，进而求出扩大后的面积。
【解答】解：200×（16÷8+1）
＝200×（2+1）
＝200×3
＝600（平方米）
答：扩大后的草坪的面积是600平方米。
【点评】此题主要考查长方形面积公式的灵活运用，积的变化规律及应用。
【变式训练03】李爷爷家有一块长方形菜地如图，长65米，宽30米。现爷爷想再种一些月季花，打算把宽增加5米，长不变。请你在图中画出种月季花的部分，并计算增加部分的面积。

【分析】根据题意可知，长不变，宽增加5米，再宽边处再往下画5米，然后连成一个大长方形，求增加部分的面积就是求长是65米，宽是5米的长方形的面积，根据长方形的面积＝长×宽即可解答。
【解答】解：画图如下：

65×5＝325（平方米）
答：增加部分的面积是325平方米。
【点评】本题考查了长方形面积公式的灵活运用。


一．选择题（共5小题）
1．边长是1分米的正方形，面积是1平方分米，可以写成（　　）
A．1bm2 B．1cm2 C．1dm2 D．无选项
【分析】根据我们学过的单位都可以用规定的字母来代替，因边长是1分米的正方形，面积是1平方分米，即规定平方分米用dm2来代替，由此解答．
【解答】解：1×1＝1（平方分米）＝1dm2，
故选：C。
【点评】解答此题关键是记住各单位都有自己的字母表示形式．
2．下面（　　）的面积大约3平方米。
A．课桌面 B．黑板面 C．餐巾纸 D．手机面
【分析】物体所占平面的大小叫做物体的面积，根据生活中物体面的大小选择，据此解答。
【解答】解：黑板面的面积大约是3平方米。
故选：B。
【点评】本题考查了面积的认识及根据生活经验判断。
3．把面积为1平方米的正方形平均分成10份，每份的面积是（　　）
A．10平方厘米 B．10平方分米 C．1平方分米
【分析】根据1平方米＝100平方分米，据此解答即可。
【解答】解：1平方米＝100平方分米
100÷10＝10（平方分米）
答：每份的面积是10平方分米。
故选：B。
【点评】熟练掌握面积单位的换算，是解答此题的关键。
4．一个长方形花坛的面积是96平方米，扩建时长不变，宽由4米增加到12米，扩建后花坛的面积是（　　）平方米。
A．384 B．1152 C．288
【分析】先根据“长方形的长＝面积÷宽”，求出这个花坛的长，再根据“长方形面积＝长×宽”计算出扩建后花坛的面积。
【解答】解：96÷4＝24（米）
24×12＝288（平方米）
答：扩建后花坛的面积是288平方米。
故选：C。
【点评】此题主要考查灵活运用长方形面积公式的能力。
5．如图长方形中每个正方形的边长都是1厘米，那么这个长方形的面积是（　　）平方厘米。

A．20 B．15 C．12 D．10
【分析】先数出长方形的长和宽里包含几个1厘米的正方形，它的长和宽就是几厘米，再根据长方形的面积公式：S＝ab，把数据代入公式求出它的面积是多少平方厘米即可。
【解答】解：5×3＝15（平方厘米）
答：这个长方形的面积是15平方厘米。
故选：B。
【点评】此题主要考查长方形面积公式的灵活运用，关键是确定长方形的长和宽。
二．填空题（共5小题）
6．把一块边长为4分米的正方形玻璃，割成大小相等的两块长方形，每块长方形的面积是　8　平方分米，周长是　12　分米．
【分析】（1）根据题意知道，割成的长方形的长是4分米，宽是4÷2分米，由此根据长方形的面积公式S＝ab，即可求出每块长方形的面积；
（2）根据长方形的周长公式C＝（a+b）×2，即可求出周长．
【解答】解：（1）长方形的面积：4×（4÷2），
＝4×2，
＝8（平方分米）；
长方形的周长：（4+4÷2）×2，
＝（4+2）×2，
＝6×2，
＝12（分米）；
答：每块长方形的面积是8平方分米；周长是12分米；
故答案为：8；12．
【点评】此题主要考查了长方形的面积公式S＝ab与长方形的周长公式C＝（a+b）×2的实际应用．
7．3平方米＝　30000　平方厘米．
【分析】把3平方米换算成平方厘米数，用3乘进率10000．
【解答】解：3平方米＝30000平方厘米；
故答案为：30000．
【点评】此题考查名数的换算，把高级单位的名数换算成低级单位的名数，就乘单位间的进率，把低级单位的名数换算成高级单位的名数，就除以单位间的进率．
8．要扩大一块长方形绿地的面积，长由原来的20米增加到100米，宽不变。绿地扩大后的面积是600平方米，扩大前的面积是 　120　平方米。
【分析】根据题意可知，用扩大后的面积除以扩大后的长求出原来长方形的宽是多少米，原来的长已知为20米，根据长方形的面积公式：S＝ab进行计算即可得到答案。
【解答】解：600÷100＝6（米）
20×6＝120（平方米）
答：扩大前的面积是120平方米。
故答案为：120。
【点评】解答此题的关键是求出原来长方形的宽是多少米。
9．如图的图形中，你觉得用第 　③　种图形作面积单位最合适。理由是 　边长为1厘米的正方形面积是1平方厘米，正方形可以密铺　。

【分析】根据物体的表面或封闭图形的大小，叫做它们的面积；常用的面积单位有：平方米、平方分米、平方厘米，可得用小正方形的面积作单位测量图形的面积最合适，据此判断即可。
【解答】解：如图的图形中，你觉得用第③种图形作面积单位最合适。理由是：边长为1厘米的正方形面积是1平方厘米，正方形可以密铺。
故答案为：②，边长为1厘米的正方形面积是1平方厘米，正方形可以密铺。
【点评】此题主要考查了面积和面积单位，要熟练掌握，解答此题的关键是要明确：用小正方形的面积作单位测量封闭图形的面积最合适。
10．边长 　1　米的正方形的面积是1平方米。
【分析】根据正方形的面积＝边长×边长，解答此题即可。
【解答】解：因为1×1＝1（平方米）
所以这个正方形的边长是1米。
故答案为：1。
【点评】熟练掌握正方形的面积公式，是解答此题的关键。
三．判断题（共5小题）
11．物体的表面或图形的大小就是它们的面积．　√　．
【分析】根据面积的意义即可作出判断．
【解答】解：物体表面或平面图形的大小，叫做它们的面积．
故答案为：√．
【点评】此题考查面积的意义：物体表面或平面图形的大小．
12．一间卧室地面的面积大约有30平方分米。 　×　
【分析】较大物体表面的面积用平方米做单位，较小物体表面的面积用平方分米或平方厘米做单位，房间的面积应用平方米做单位。
【解答】解：一间卧室地面的面积大约有30平方米。原题说法错误。
故答案为：×。
【点评】本题考查了面积单位的选择，注意根据生活情境选择。
13．边长是100分米的正方形的面积是1平方米．　×　
【分析】把分米换算成米，然后用边长乘边长求出面积后再判断即可．
【解答】解：100分米＝10米，10×10＝100（平方米），
原题说法错误．
故答案为：×．
【点评】此题主要考查正方形的面积的计算方法，关键是注意单位的换算．
14．周长相等的两个正方形，它们的面积一定相等。 　√　
【分析】两个正方形的周长相等，根据正方形的周长公式：周长＝边长×4，那么两个正方形的边长就一定相等，则两个正方形的面积就相等；由此得出判断。
【解答】解：正方形的周长：周长＝边长×4
边长＝周长÷4
所以两个正方形的周长相等，边长就一定相等，
再根据正方形的面积＝边长×边长，
所以两个正方形的面积相等，
所以“周长相等的两个正方形，它们的面积一定相等”的说法是正确的。
故答案为：√。
【点评】本题运用正方形的周长及面积公式解答即可。
15．一个正方形的边长增加5厘米，它的面积就增加25平方厘米。 　×　
【分析】如图：增加的面积分为三部分，即长为m厘米，宽是5厘米两个长方形的面积和一个边长是5厘米的正方形的面积；由此解答即可。

【解答】解：如图：

增加的面积是：
5m+5m+5×5
＝10m+25（平方厘米）
所以原题说法错误。
故答案为：×。
【点评】此题可以通过画图进行分析解答比较容易理解。
四．计算题（共1小题）
16．计算下列各图的周长和面积。

【分析】（1）这是一个边长是9厘米的正方形，根据正方形的周长＝边长×4，以及正方形的面积＝边长×边长进行求解；
（2）这是一个长是16厘米，宽是6厘米的长方形，根据长方形的周长＝（长+宽）×2，以及长方形的面积＝长×宽进行求解。
【解答】解：（1）9×4＝36（厘米）
9×9＝81（平方厘米）
答：正方形的周长是36厘米，面积是81平方厘米。
（2）（16+6）×2
＝22×2
＝44（厘米）
16×6＝96（平方厘米）
答：长方形的周长是44厘米，面积是96平方厘米。
【点评】解决本题关键是熟练掌握长方形、正方形的周长公式和面积公式。
五．应用题（共4小题）
17．一块长方形菜地，长15米，宽8米。菜地扩建后宽增加了2米，长不变，现在这块长方形菜地的面积是多少平方米？（用两种方法解答）
【分析】（1）根据题意，原来的宽是8米，宽增加了2米，现在的宽10米，根据长方形的面积＝长×宽进行计算即可。
（2）根据长方形的面积公式，求出原来长方形的面积和后来增加的长方形面积，用原来长方形的面积加上增加的长方形的面积就是增加后的面积。
【解答】解：（1）15×（8+2）
＝15×10
＝150（平方米）
（2）15×8+15×2
＝120+30
＝150（平方米）
答：现在这块长方形菜地的面积是150平方米。
【点评】本题主要是利用长方形的面积解决问题。
18．聪聪的书桌长90cm，宽50cm。如果书桌的长不变，宽增加20cm，那么增加后的书桌面积是多少平方厘米？合多少平方分米？合多少平方米？
【分析】先求出增加后的宽，再根据长方形的面积公式：S＝ab，把数据代入公式求出它的面积是多少平方厘米，然后换算成用平方分米、平方米作单位即可。
【解答】解：90×（50+20）
＝90×70
＝6300（平方厘米）
6300平方厘米＝63平方分米
63平方分米＝0.63平方米
答：增加后的书桌面积是6300平方厘米，合63平方分米，0.63平方米。
【点评】此题主要考查长方形面积公式的灵活运用，关键是熟记公式，注意：相邻面积单位之间的进率及换算。
19．小区前面有一块边长是30米的正方形空地，现要在空地的中间做一个长20米，宽16米的长方形花圃，其余的植上草皮。（如图）
（1）花圃的周长是多少米？
（2）草皮的面积是多少平方米？

【分析】（1）根据长方形的周长＝（长+宽）×2，求出周长即可；
（2）算出正方形和长方形的面积，再相减即可。
【解答】解：（1）（20+16）×2
＝36×2
＝72（米）
答：花圃的周长是72米。
（2）30×30﹣20×16
＝900﹣320
＝580（平方米）
答：草皮的面积是580平方米。
【点评】熟练掌握长方形和正方形的周长和面积公式，是解答此题的关键。
20．一台收割机每分行驶28m，收割宽度是5m。这台收割机行驶9分收割的面积是多少平方米？
【分析】首先根据长方形的面积＝长×宽，把数据代入公式求出每分钟收割的面积，然后再乘收割的时间即可。
【解答】解：28×5×9
＝140×9
＝1260（平方米）
答：这台收割机行驶9分收割的面积是1260平方米。
【点评】此题主要考查长方形面积公式的灵活运用，关键是熟记公式。

一．选择题（共5小题）
1．用5个1平方厘米的正方形，拼成下面的图形，它们的面积相比，（　　）

A．第一个图形大 B．第二个图形大
C．一样大
【分析】用5个1平方厘米的正方形拼成的图形，无论怎么拼，拼成图形的面积都是1×5＝5（平方厘米），由此求解．
【解答】解：拼成图形的面积是1×5＝5（平方厘米）
所以拼成的图形的面积都相等；
故选：C。
【点评】抓住图形拼组的特点：拼组后面积不变进行求解．
2．（　　）的面积最接近1平方分米．
A．指甲 B．粉笔盒底面 C．课本封面 D．方凳面
【分析】根据生活经验可知，指甲的面积接近1平方厘米，粉笔盒底面接近1平方分米，课本封面接近10平方分米，方凳面接近30平方分米，由此选择即可．
【解答】解：根据生活经验由分析可知，粉笔盒底面接近1平方分米；
故选：B。
【点评】此题考查名数的换算，把高级单位的名数换算成低级单位的名数，就乘单位间的进率；把低级单位的名数换算成高级单位的名数，就除以单位间的进率．
3．8平方分米+4平方厘米＝（　　）
A．84平方分米 B．804平方厘米
【分析】不同单位的名数相加，要先化成相同单位的名数再计算．
【解答】解：8平方分米+4平方厘米
＝800平方厘米+4平方厘米
＝804平方厘米．
故选：B．
【点评】不同单位的名数相加，要先化成相同单位的名数再计算，化成什么单位要根据题意或实际情况．
4．请估一估，你所在教室地面的面积大约是60（　　）
A．平方米 B．平方厘米 C．平方分米 D．立方厘米
【分析】根据生活经验、对面积单位和数据大小的认识，计量教室地面面积大约是60平方米，据此解答即可．
【解答】解：教室地面的面积大约是60平方米．
故选：A．
【点评】此题考查根据情景选择合适的计量单位，要注意联系生活实际、计量单位和数据的大小，灵活的选择．
5．小区里有一块供居民运动的空地（如图），面积是200平方米。为了增大居民们的运动空间，要扩建运动空地，运动空地的长要增加到35米，宽不变。扩建后运动空地的面积增加了（　　）

A．280平方分米 B．280平方米
C．80平方分米 D．80平方米
【分析】根据长方形的面积＝长×宽，先求出原来的宽，再求出增加的长，然后把数据代入公式解答。
【解答】解：（35﹣25）×（200÷25）
＝10×8
＝80（平方米）
答：扩建后运动空地的面积增加了80平方米。
故选：D。
【点评】此题主要考查长方形面积公式的灵活运用，关键是熟记公式。
二．填空题（共5小题）
6．小明绕一块正方形草地走了4圈，共走了1600米，这块正方形草地的面积是 　10000　平方米。
【分析】首先求出正方形的周长，用正方形的周长除以4求出正方形的边长，然后根据正方形的面积＝边长×边长，把数据代入公式解答。
【解答】解：1600÷4÷4
＝400÷4
＝100（米）
100×100＝10000（平方米）
答：这块正方形草地的面积是10000平方米。
故答案为：10000。
【点评】此题主要考查正方形的周长公式、面积公式的灵活运用，关键是熟记公式。
7．一块长方形铁皮，长16厘米，宽9厘米，从它上面剪下一个最大的正方形，这个正方形的面积是 　81　平方厘米，剩下部分的面积是 　63　平方厘米。
【分析】根据题意可知，从这块长方形铁皮上剪下一个最大的正方形，这个正方形的边长等于长方形的宽，根据正方形的面积＝边长×边长，长方形的面积＝长×宽，把数据代入公式解答。
【解答】解：9×9＝81（平方厘米）
9×（16﹣9）
＝9×7
＝63（平方厘米）
答：这个正方形的面积是81平方厘米，剩下部分的面积是63平方厘米。
故答案为：81，63。
【点评】此题主要考查正方形、长方形面积公式的灵活运用，关键是熟记公式。
8．5平方米＝　50000　平方厘米
7000平方厘米＝　70　平方分米．
【分析】（1）高级单位平方米化低级单位平方厘米乘进率10000．
（2）低级单位平方厘米化高级单位平方分米除以进率100．
【解答】解：（1）5平方米＝50000平方厘米；
（2）7000平方厘米＝70平方分米．
故答案为：50000，70．
【点评】平方米、平方分米、平方厘米相邻单位间的进率是100，由高级单位化低级单位乘进率，反之除以进率．
9．（1）下面方格中哪个图形的面积最大？请打“√”

（2）若每格是1cm2，图①的面积是　6　cm2，图②的面积是　8　cm2．
【分析】（1）因每个格是1平方厘米所以每个格子的长是1厘米，长方形的面积是5×2＝10厘米，平行四边形的面积看作是两个三角形的面积4×2÷2×2＝8平方厘米，三角形的面积是4×3÷2＝6平方厘米，梯形的面积是（5+3）×2÷2＝8平方厘米．所以长方形的面积最大．
（2）每个方格是1平方厘米，图①的面积是长为4厘米，宽为3厘米的长方形面积的一半，图②的面积是8平方厘米．
【解答】解：（1）

（2）图①的面积是6cm2，图②的面积是8cm2．
故答案为：6，8．
【点评】本题主要考查了学生对方格图中图形面积计算方法的掌握情况．
10．长5厘米，宽4厘米的长方形，面积是 　20　平方厘米。
【分析】根据长方形的面积＝长×宽，把数据代入计算即可解答。
【解答】解：5×4＝20（平方厘米）
答：面积是20平方厘米。
故答案为：20。
【点评】熟练掌握长方形的面积公式是解答本题的关键。
三．判断题（共5小题）
11．小丽的数学课本面积约是3平方分米　√　
【分析】根据生活经验、对面积单位和数据大小的认识，可知计量数学课本封面的面积，应用面积单位，结合数据可知：应用“平方分米”作单位；据此判断．
【解答】解：由分析知：数学课本封面的面积约3平方分米，原题说法正确．
故答案为：√．
【点评】此题考查根据情景选择合适的计量单位，要注意联系生活实际、计量单位和数据的大小，灵活的选择．
12．两个面积单位间的进率是10．　×　
【分析】常用面积单位平方米、平方分米、平方厘米相邻单位间的进率是100．
【解答】解：两个面积单位间的进率是100，原题的说法是错误的．
故答案为：×．
【点评】平方米、平方分米、平方厘米相邻单位间的进率是100．由高级单位化低级单位乘进率，反之除以进率．
13．如图是我国珍贵的历史文化遗产《易经》中的一个主要图形﹣﹣﹣太极图，它是数形结合的光辉典范．图中阴阳（即圈内黑白）两部分的面积相等．　√　

【分析】因为太极图是旋转对称图形，即一条白鱼和黑鱼的面积相等，然后同时加上一个小圆的面积（眼睛），可得：图中阴阳（即圈内黑白）两部分的面积相等；由此即可判断．
【解答】解：由分析可知：图中阴阳（即圈内黑白）两部分的面积相等；
故答案为：√．
【点评】本题考查了旋转对称图形：如果某一个图形围绕某一点旋转一定的角度（小于360°）后能与原图形重合，那么这个图形就叫做旋转对称图形．常见的旋转对称图形有：线段，正多边形，平行四边形，圆等．
14．物体的表面或图形的大小就是它们的面积．　×　
【分析】根据面积的意义，物体表面或平面图形的大小叫做它们的面积．据此判断即可．
【解答】解：由分析得：
物体表面或平面图形的大小叫做它们的面积．
因此，物体的表面或图形的大小就是它们的面积．这种说法是错误的．
故答案为：×．
【点评】此题考查的目的是理解掌握面积的意义及应用．
15．用一根长20厘米的铁丝围成形状不同的长方形，他们的面积相等。 　×　
【分析】根据长方形的周长＝（长+宽）×2，那么长+宽＝周长÷2，据此求出长与宽的和，再根据长方形的面积＝长×宽，分别求出它们的面积，然后进行比较即可。
【解答】解：20÷2＝10（厘米）
10＝9+1＝8+2＝7+3＝6+4
9×1＝9（平方厘米）
8×2＝16（平方厘米）
7×3＝21（平方厘米）
6×4＝24（平方厘米）
所以它们的面积不相等。
因此题干中的结论是错误的。
故答案为：×。
【点评】此题主要考查长方形的周长公式、面积公式的灵活运用，关键是熟记公式。
四．计算题（共1小题）
16．计算图形的周长和面积

【分析】（1）图一是正方形，边长是64米，根据正方形的周长公式：C＝4a，正方形的面积公式：S＝a2，进行计算即可．
（2）图二的周长是所有线段的和，把所有的线段的长度相加即可，相当于长是36米，宽是24米的长方形的周长加上两条长6米的线段，面积是长36米，宽24米的长方形的面积减去长12米，宽6米的长方形的面积，根据长方形的面积公式S＝ab解答即可．
【解答】解：（1）周长：
64×4＝256（米）
面积：
64×64＝4096（平方米）
答：周长是256米，面积是4096平方米．
（2）周长：
（36+24）×2+6×2
＝60×2+12
＝120+12
＝132（米）
面积：
36×24﹣12×6
＝864﹣72
＝792（平方米）
答：周长是132米，面积是792平方米．
【点评】本题主要考查了学生对长方形和正方形周长及面积计算方法的掌握．
五．应用题（共4小题）
17．一块长方形试验田，宽20米，面积960平方米。后来要扩大试验田，把它的宽增加到40米，长不变。扩大后的试验田面积是多少平方米？
【分析】根据长方形的面积公式：S＝ab，用原来的面积除以宽求出长，再用长乘扩建后的宽即可求出扩建后的面积。
【解答】解：960÷20×40
＝48×40
＝1920（平方米）
答：扩大后的试验田面积是1920平方米。
【点评】此题主要考查长方形面积公式的灵活运用，关键是熟记公式。
18．红红家装修房子，她家的客厅长9米，宽6米。如果用边长为3分米的地砖铺地，一共需要多少块？
【分析】根据除法的面积＝长×宽，求出客厅地面的面积，根据正方形的面积＝边长×边长，求出每块地砖的面积，然后根据“包含”除法的意义，用除法解答。
【解答】解：9×6＝54（平方米）
54平方米＝5400平方分米
5400÷（3×3）
＝5400÷9
＝600（块）
答：一共需要600块。
【点评】此题主要考查长方形、正方形面积公式的灵活运用，关键是熟记公式。
19．为创建“全国文明城市”，龙泉公园扩建一块长方形草坪（如图），把宽增加到32米，长不变，扩建后的草坪面积比原来增加了多少平方米？

【分析】根据长方形的面积＝长×宽，那么长＝面积÷宽，据此求出原来的长，再求出增加部分的宽，然后把数据代入公式解答。
【解答】解：480÷8＝60（米）
60×（32﹣8）
＝60×24
＝1440（平方米）
答：扩建后的草坪面积比原来增加了1440平方米。
【点评】此题主要考查长方形面积公式的灵活运用，关键是熟记公式。
20．一块320平方米的长方形草坪，宽8米，现在要扩大面积，长不变，宽要增加到24米。扩大后的草坪面积是多少？
【分析】根据长方形的面积＝长×宽，再根据积的变化规律，一个因数不变，另一个因数扩大到原来的几倍，积就扩大到原来的几倍，先求出扩大后的宽是原来宽几倍，进而求出扩大后面积。
【解答】解：320×（24÷8）
＝320×3
＝960（平方米）
答：扩大后的草坪面积是960平方米。
【点评】此题主要考查长方形面积公式的灵活运用，积的变化规律及应用.

一．选择题（共5小题）
1．（2022春•醴陵市期末）把面积为1平方米的正方形平均分成10份，每份的面积是（　　）
A．10平方厘米 B．10平方分米 C．1平方分米
【分析】根据1平方米＝100平方分米，据此解答即可。
【解答】解：1平方米＝100平方分米
100÷10＝10（平方分米）
答：每份的面积是10平方分米。
故选：B。
【点评】熟练掌握面积单位的换算，是解答此题的关键。
2．（2021秋•龙口市期末）（　　）的面积最接近1平方厘米。
A．计算机键盘上一个按键面
B．课桌面
C．粉笔盒的一个面
D．教室地面
【分析】根据生活实际情况，计算机键盘上一个按键面的面积最接近1平方厘米，据此解答即可。
【解答】解：计算机键盘上一个按键面的面积最接近1平方厘米。
故选：A。
【点评】此类问题要联系实际，不能和实际相违背。
3．（2022春•马山县期末）刘阿姨家铺地板用了120块地砖，李阿姨家铺地板用了136块地砖。下面说法正确的是（　　）
A．刘阿姨家面积比较大 B．李阿姨家面积比较大
C．无法判断谁家面积更大
【分析】瓷砖大小不一定一样，因此房子的面积也就不一定一样，据此根据生活经验判断。
【解答】解：光依据瓷砖的多少判断房子面积大小是不能比较的。
故选：C。
【点评】本题考查了面积在生活中的应用。
4．（2022春•阳泉期中）聪聪用数学书去测量一个物体表面的大小，铺满这个物体表面刚好用了30本数学书，这个物体表面的面积大约是（　　）
A．90平方分米 B．9平方米
C．150平方分米 D．1500平方厘米
【分析】数学书封面，长约25厘米，宽约20厘米，面积约是：25×20＝500（平方厘米），据此解答即可。
【解答】解：数学书封面，长约25厘米，宽约20厘米，面积约是：25×20＝500（平方厘米）。
500平方厘米＝5平方分米
5×30＝150（平方分米）
答：这个物体表面的面积大约是150平方分米。
故选：C。
【点评】知道数学书封面的面积，是解答此题的关键。
5．（2022秋•莱阳市期末）长方形和正方形的周长相等，那么（　　）的面积大。
A．长方形 B．正方形 C．一样大 D．不确定
【分析】本题要判断对错，首先进行假设，假设周长是16厘米，进而根据长方形和正方形的面积进行分析、判断，得出结论。
【解答】解：假设周长都是16厘米，则正方形的边长：16÷4＝4（厘米），面积：4×4＝16（平方厘米）；
假设长方形的长为6厘米，宽为2厘米，则面积：2×6＝12（平方厘米）；
长方形的面积＜正方形的面积。
故选：B。
【点评】此题没有数据，分析时应假设出周长，然后根据面积公式进行分析，进而得出问题答案；注意：周长相等的长方形和正方形，所围成的面积，正方形大。
二．填空题（共5小题）
6．（2019春•庆云县期末）（1）一张电话卡的面积大约是40 　平方厘米　．
（2）教室长8 　米　，宽6 　米　，面积是 　48平方米　．
【分析】根据生活经验、对长度单位，面积单位和数据大小的认识，可知计量一张电话卡的面积用“平方厘米”作单位；计量教室长用“米”作单位，计量教室宽用“米”作单位；计量面积用“平方米”作单位，据此解答即可．
【解答】解：（1）一张电话卡的面积大约是40平方厘米；
（2）教室长8米，宽6米，面积是48平方米．
故答案为：平方厘米；米、米，48平方米．
【点评】此题考查根据情景选择合适的计量单位，要注意联系生活实际、计量单位和数据的大小，灵活的选择．
7．（2021春•中牟县期末）如图中，每个小方格表示1平方厘米。数一数，比一比，图 　③　的面积最大，图 　②　的面积最小。

【分析】利用数格子的方法比较面积大小，两个半格算一格，据此解答。
【解答】解：图一的面积为8平方厘米；图二的面积为6平方厘米；图三的面积为9平方厘米。因此图③的面积最大，图②的面积最小。
故答案为：③，②。
【点评】本题考查了利用数格子比较图形的面积大小。
8．（2022秋•莱阳市期末）两个边长为4dm的正方形拼成一个长方形，它的周长是 　24分米　，面积是 　32平方分米　。
【分析】两个边长4分米的正方形拼成一个长方形，长方形的长是正方形边长的2倍，宽和正方形边长相等，由此再根据长方形周长＝（长+宽）×2，长方形的面积＝长×宽，代入数据解答即可。
【解答】解：长方形的长是：4×2＝8（分米），宽是4分米；
（8+4）×2
＝12×2
＝24（分米）
8×4＝32（平方分米）
答：长方形的周长是24分米，面积是32平方分米。
故答案为：24分米，32平方分米。
【点评】根据拼组的方法，找出拼成长方形的长、宽与正方形边长的关系，进而根据长方形周长和面积的计算方法解答即可。
9．（2022春•新会区期末）一个正方形的周长是36分米，它的面积是 　81　平方分米。
【分析】根据正方形周长公式，正方形周长＝边长×4，用除法计算出边长，再根据边长乘边长就是面积，据此解答。
【解答】解：36÷4＝9（分米）
9×9＝81（平方分米）
答：它的面积是81平方分米。
故答案为：81。
【点评】熟练掌握正方形周长以及面积的计算公式并灵活运用是解答本题的关键。
10．（2021春•迪庆州期末）800平方分米＝　8　平方米；
700平方厘米＝　7　平方分米；
150000平方厘米＝　15　平方米。
【分析】低级单位平方分米化高级单位平方米除以进率100。
低级单位平方厘米化高级单位平方分米除以进率100。
低级单位平方厘米化高级单位平方米除以进率10000。
【解答】解：800平方分米＝8平方米；
700平方厘米＝7平方分米；
150000平方厘米＝15平方米。
故答案为：8，7，15。
【点评】平方米、平方分米、平方厘米相邻单位间的进率是100，由高级单位化低级单位乘进率，反之除以进率。
三．判断题（共5小题）
11．（2022春•蓬江区月考）用10个面积为1平方厘米的小正方形拼成图形，它们的面积都是10平方厘米。 　√　
【分析】根据正方形的面积＝边长×边长，把数据代入公式求出一个小正方形的面积，然后再乘小正方形的个数就是拼成图形的面积。据此判断。
【解答】解：1×1×10＝10（平方厘米）
答：它的面积是10平方厘米。
因此题干中的结论是正确的。
故答案为：√。
【点评】此题主要考查正方形面积公式的灵活运用，关键是熟记公式。
12．（2021春•唐河县期末）面积为1平方米的正方形的边长为10分米。 　√　
【分析】因为1米×1米＝1平方米，所以边长是1米的正方形面积是1平方米，据此即可解答。
【解答】解：因为1米×1米＝1平方米，所以边长是1米的正方形面积是1平方米，1米＝10分米，所以本题说法正确。
故答案为：√。
【点评】此题主要考查正方形的面积公式的计算应用，熟记公式即可解答。
13．（2022春•惠州期末）1000平方厘米＞20平方分米 　×　
【分析】1000平方厘米＝10平方分米，再用10平方分米与20平方分米比较。
【解答】解：1000平方厘米＜20平方分米
原题说法错误。
故答案为：×。
【点评】不同单位的名数的大小比较通常是先化成相同的单位名数，再根据数值的大小进行比较。
14．（2022秋•平利县期末）边长是4厘米的正方形周长和面积相等。 　×　
【分析】根据周长和面积的定义分析判断即可。
【解答】解：边长是4厘米的正方形，正方形周长＝边长×4，正方形面积＝边长×边长，意义不同，周长和面积无法比较，原题说法错误。
故答案为：×。
【点评】明确找出和面积是不同的量是解题的关键。
15．（2022秋•峄城区期中）正方形的边长是20米，将边长增加到40米后，面积扩大到原来的2倍。 　×　
【分析】根据正方形的面积＝边长×边长，把数据代入公式分别求出原来的面积、增加后的面积，然后根据求一个数是另一个数的几倍，用除法求出扩大后的面积是原来面积的多少倍。据此判断。
【解答】解：40×40÷（20×20）
＝1600÷400
＝4
所以面积扩大到原来的4倍。
因此题干中的结论是错误的。
故答案为：×。
【点评】此题主要考查正方形面积公式的灵活运用，关键是熟记公式。
四．计算题（共1小题）
16．（2021秋•肥城市期末）求出下面图形的周长和面积。

【分析】把这个图形补成一个长是10厘米，宽是7厘米的长方形，这个图形的周长就等于补成的长方形的周长，面积就等于补成的长方形的面积，减去边长是5厘米的正方形的面积即可。
【解答】解：

（10+5+2）×2
＝17×2
＝34（厘米）
10×（5+2）﹣5×5
＝70﹣25
＝45（平方厘米）
答：周长是34厘米，面积是45平方厘米。
【点评】熟练掌握长方形和正方形的周长和面积公式，是解答此题的关键。
五．应用题（共4小题）
17．（2022秋•略阳县期末）学校的苗圃长17米，宽5米，平均每平方米种2株杜鹃花，一共可以种多少株杜鹃花？
【分析】先利用长方形的面积公式：S＝ab求出苗圃的面积，再用苗圃的面积乘每平方米树苗的棵数，列式解答即可。
【解答】解：17×5×2
＝85×2
＝170（株）
答：一共可以种170株杜鹃花。
【点评】此题主要考查长方形的面积的计算方法在实际生活中的应用。
18．（2021秋•莱州市期末）一个长方形的果园宽22米，长是宽的2倍。
（1）如果在果园四周围上那个栅栏，一共需要多少米栅栏？
（2）果园的占地面积是多少平方米？
（3）如果每棵果树占地4平方米，这个果园能种多少棵果树？
【分析】（1）先求出这个果园长边的长度，再根据“长方形周长＝（长+宽）×2”，即可求出栅栏的长度。
（2）根据“长方形面积＝长×宽”，即可求出这个果园的面积。
（3）用果园的面积除以4，即可求出这个果园能种多少棵果树。
【解答】解：（1）（22×2+22）×2
＝（44+22）×2
＝66×2
＝132（米）
答：一共需要132米栅栏。
（2）22×2×22
＝44×22
＝968（平方米）
答：果园的占地面积是968平方米。
（3）968÷4＝242（棵）
答：这个果园能种242棵果树。
【点评】熟记长方形的周长、面积计算公式，是解答此题的关键。
19．（2022秋•留坝县期末）一台收割机的作业宽度是2m，这台收割机每小时行5km，需要多少小时可以收割完下面这块地的小麦？（单位：米）

【分析】5千米＝5000米，如图：用大正方形的面积减去边长为（200﹣100）米的正方形的面积，求出这块地的面积，根据长方形的面积＝长×宽求出收割机每小时收割的面积，最后再用这块地的面积除以收割机每小时收割的面积即可得到答案。
【解答】解：200×200﹣（200﹣100）×（200﹣100）
＝40000﹣100×100
＝40000﹣10000
＝30000（平方米）
5千米＝5000米
30000÷（5000×2）
＝30000÷10000
＝3（小时）
答：需要3小时可以收割完。
【点评】解答此题的关键是确定田的面积和收割机每小时收割的面积，用田的面积除以收割机每小时收割的面积即可。
20．（2022秋•莱阳市期末）王伯伯打算搭建一个长24米，宽12米的塑料大棚种蔬菜，由于疫情影响，减少了搭建规模，长缩小了6米，宽不变。
（1）王伯伯现在搭建的塑料大棚的占地面积是多少平方米？
（2）为了让大棚更牢固，王伯伯又围绕大棚的底部四周进行了加固，如果每米加固条15元，请你帮忙算一算王伯伯一共需要花费多少元买加固条。
【分析】（1）先求出缩小后的长是多少米，再根据长方形的面积＝长×宽，把数据代入公式解答。
（2）根据长方形的周长＝（长+宽）×2，把数据代入公式求出这个大棚的周长，然后再乘每米的费用即可。
【解答】解：（1）24﹣6＝18（米）
18×12＝216（平方米）
答：王伯伯现在搭建的塑料大棚的占地面积是216平方米。
（2）（18+12）×2×15
＝30×2×15
＝60×15
＝900（元）
答：王伯伯一共需要花费900元买加固条。
【点评】此题主要考查长方形的面积公式、周长公式的灵活运用，关键是熟记公式。