【中考化学】2023届北京市海淀区专项突破模拟仿真试题练习（含解析）

展开

这是一份【中考化学】2023届北京市海淀区专项突破模拟仿真试题练习（含解析）
【中考化学】2023届北京市海淀区专项突破模拟仿真试题练习
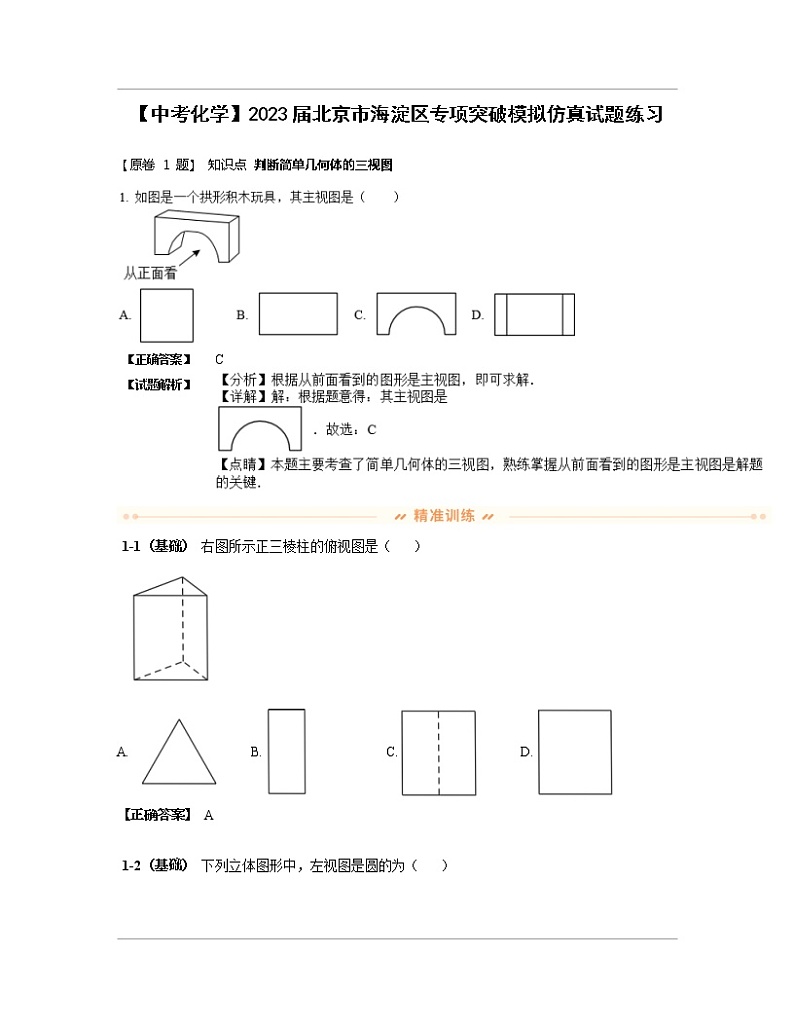
【原卷 1 题】知识点判断简单几何体的三视图

【正确答案】
C
【试题解析】

1-1（基础）右图所示正三棱柱的俯视图是（）

A. B. C. D.
【正确答案】 A

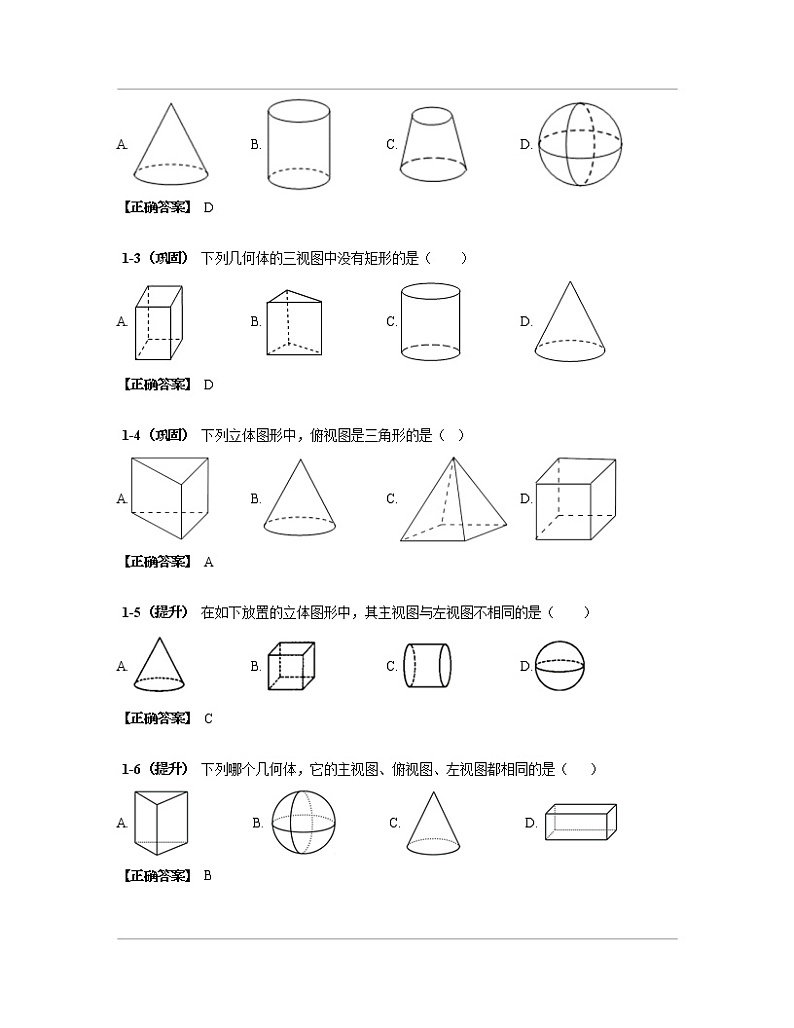
1-2（基础）下列立体图形中，左视图是圆的为（）
A. B. C. D.
【正确答案】 D

1-3（巩固）下列几何体的三视图中没有矩形的是（　　）
A. B. C. D.
【正确答案】 D

1-4（巩固）下列立体图形中，俯视图是三角形的是（）
A. B. C. D.
【正确答案】 A

1-5（提升）在如下放置的立体图形中，其主视图与左视图不相同的是（　　）
A. B. C. D.
【正确答案】 C

1-6（提升）下列哪个几何体，它的主视图、俯视图、左视图都相同的是（）
A. B. C. D.
【正确答案】 B

【原卷 2 题】知识点用科学记数法表示绝对值大于1的数

【正确答案】
B
【试题解析】

2-1（基础）我国成功发射北斗系统第55颗导航卫星，暨北斗三号最后一颗全球组网卫星，该卫星距离地面约36000千米．将36000用科学记数法表示应为（　　）
A.3.6×103 B.3.6×104 C.36×103 D.0.36×105
【正确答案】 B

2-2（基础） 5G是第五代移动通信技术，5G网络理论下载速度可以达到每秒1300000KB以上．用科学记数法表示1300000是（　　）
A. B. C. D.
【正确答案】 C

2-3（巩固） 2021年12月9日15时40分，“天宫课堂”第一课开始，神舟十三号乘组航天员翟志刚、王亚平、叶光富在中国空间站进行太空授课，全国超过6000万中小学生观看授课直播，其中6000万用科学记数法表示为（　　）
A.6000×104 B.6×107 C.0.6×108 D.6×108
【正确答案】 B

2-4（巩固） 2019年4月17日，国家统计局公布2019年一季度中国经济数据．初步核算，一季度国内生产总值213433亿元，按可比价格计算，同比增长6.4%．数据213433亿用科学记数法表示应为（　　）
A.2.13433×1013 B.0.213433×1014
C.213.433×1012 D.2.13433×1014
【正确答案】 A

2-5（提升） 2018年第一季度北京市地区生产总值中第三产业增加值约5590亿元，第二季度较上一季度增长7%，则第二季度第三产业增加值用科学记数法表示约为（）
A.元 B.元 C.元 D.元
【正确答案】 D

2-6（提升）截止到年月日时，全球感染新型冠状肺炎的人数已经达到人，携手抗击疫情，刻不容缓．请将精确到万位，用科学记数法表示为（）
A. B. C. D.
【正确答案】 B

【原卷 3 题】知识点几何图形中角度计算问题,角平分线的有关计算

【正确答案】
B
【试题解析】

3-1（基础）如图，已知，，则的度数为( )

A. B. C. D.
【正确答案】 B

3-2（基础）如图，直线，交于点O．射线平分，若，则等于（）

A. B. C. D.
【正确答案】 D

3-3（巩固）一副三角板如图所示摆放，若，则的度数是（）

A. B. C. D.
【正确答案】 C

3-4（巩固）如图，已知是平角，平分，在平面上画射线，使和互余，若，则的度数为（）

A. B. C.或 D.或
【正确答案】 D

3-5（提升）如图，射线OB、OC在∠AOD的内部，下列说法：
①若∠AOC＝∠BOD＝90°，则与∠BOC互余的角有2个；
②若∠AOD+∠BOC＝180°，则∠AOC+∠BOD＝180°；
③若OM、ON分别平分∠AOD，∠BOD，则∠MON＝∠AOB；
④若∠AOD＝150°、∠BOC＝30°，作∠AOP＝∠AOB、∠DOQ＝∠COD，则∠POQ＝90°
其中正确的有（　　）

A.1个 B.2个 C.3个 D.4个
【正确答案】 C

3-6（提升）入射光线和平面镜的夹角为，转动平面镜，使入射角减小，反射光线与入射光线的夹角和原来相比较将（）
A.减小 B.减小 C.减小 D.不变
【正确答案】 C

【原卷 4 题】知识点正多边形的外角问题

【正确答案】
D
【试题解析】

4-1（基础）正十边形的每一个外角的度数为（）
A. B. C. D.
【正确答案】 A

4-2（基础）正n边形的每个内角都是120°，则n的值为（）
A.8 B.7 C.6 D.5
【正确答案】 C

4-3（巩固）如图，小明从点A出发沿直线前进10米到达点B，向左转后又沿直线前进10米到达点C，再向左转后沿直线前进10米到达点D……照这样走下去，小明第一次回到出发点A时所走的路程为（）

A.100米 B.80米 C.60米 D.40米
【正确答案】 B

4-4（巩固）一个正多边形的一个内角是它相邻外角的5倍，则这个正多边形的边数是（　　）
A.12 B.10 C.8 D.6
【正确答案】 A

4-5（提升）如图，在由等边三角形、正方形和正五边形组合而成的图形中，∠3＝60°，则∠1+∠2的度数为（　　）

A.39° B.40° C.41° D.42°
【正确答案】 D

4-6（提升）如图，六边形中，的外角都相等，即，分别作和的平分线交于点P，则的度数是（）

A. B. C. D.
【正确答案】 B

【原卷 5 题】知识点根据概率公式计算概率

【正确答案】
A
【试题解析】

5-1（基础）掷一枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，掷得面朝上的点数为偶数的概率为（）
A. B. C. D.
【正确答案】 D

5-2（基础）一个不透明的盒子中装有3个红球，2个黄球和1个绿球，这些球除了颜色外无其他差别，从中随机摸出一个小球，恰好是红球的概率是（）
A. B. C. D.
【正确答案】 A

5-3（巩固）一个不透明的袋中装有8个黄球，个红球，个白球，每个球除颜色外都相同．任意摸出一个球，是黄球的概率与不是黄球的概率相同，下列与的关系一定正确的是（）
A. B. C. D.
【正确答案】 C

5-4（巩固）某公司的班车在7∶30，8∶00，8∶30从某地发车，小李在7∶50至8∶30之间到达车站乘坐班车，如果他到达发车站的时刻是随机的，则他等车时间不超过10分钟的概率是（）
A. B. C. D.
【正确答案】 B

5-5（提升）在四张质地、大小相同的卡片上，分别画有如图所示的四个图形，在看不到图形的情况下从中任意抽出一张卡片，则抽出的卡片上的图形是中心对称图形的概率为（　　）

A.1 B. C. D.
【正确答案】 B

5-6（提升）如图，在的正方形网格图中，有3个小正方形涂成了黑色，现在从白色小正方形中任意选取一个并涂成黑色，使黑色部分的图形构成一个轴对称图形的概率是( )

A. B. C. D.
【正确答案】 C

【原卷 6 题】知识点利用数轴比较有理数的大小,根据点在数轴的位置判断式子的正负,绝对值的意义

【正确答案】
B
【试题解析】

6-1（基础）如图，若点A，B，C所对应的数为a，b，c，则下列大小关系正确的是（）

A. B.
C. D.
【正确答案】 B

6-2（基础） a，b是有理数，它们在数轴上的对应点的位置如图所示，把a，b，0，按照从大到小的顺序排列，正确的是（）

A. B. C. D.
【正确答案】 D

6-3（巩固）实数a，b在数轴上的对应点的位置如图所示，则正确的结论是( )

A. B. C. D.
【正确答案】 D

6-4（巩固）若实数，，，在数轴上的对应点的位置如图所示，其中，则正确的结论是（）

A. B. C. D.
【正确答案】 D

6-5（提升）如图，数轴上的两点A、B对应的实数分别是a、b，则下列式子中成立的是（　　）

A.1﹣2a＞1﹣2b B.﹣a＜﹣b C.a+b＜0 D.|a|﹣|b|＞0
【正确答案】 A

6-6（提升）实数在数轴上对应点的位置如图所示，则正确的结论是（）

A. B. C. D.
【正确答案】 C

【原卷 7 题】知识点轴对称图形的识别,根据旋转的性质求解,中心对称图形的识别

【正确答案】
D
【试题解析】

7-1（基础）下列关于防范“新冠肺炎”的标志中既是轴对称图形，又是中心对称图形的是（）
A. B. C. D.
【正确答案】 C

7-2（基础）徽章交换是现代奥林匹克运动会特有的文化活动，深受运动员、志愿者、媒体记者及工作人员的喜爱．一枚小小的徽章不仅是参与奥运盛会的证明，更是交流奥林匹克精神与世界文化的小窗口．在2022年北京冬奥会上，徽章交换依然深受欢迎．下列徽章图案中，既是轴对称图形，又是中心对称图形的是（）
A. B.
C. D.
【正确答案】 C

7-3（巩固）北京大兴国际机场于2019年6月30日完美竣工，如图是世界著名建筑设计大师扎哈设计的机场成体俯视图的示意图．下列说法正确的是（　　）

A.这个图形是轴对称图形，但不是中心对称图形
B.这个图形是中心对称图形，但不是轴对称图形
C.这个图形既是轴对称图形，又是中心对称图形
D.这个图形既不是轴对称图形，也不是中心对称图形
【正确答案】 A

7-4（巩固） 2021年3月考古人员在山西泉阳发现目前中国规模最大、保存最完好的战国水井，井壁由等长的柏木按原始榫卯结构相互搭接呈闭合的正九边形逐层垒砌，关于正九边形下列说法错误的是（　　）

A.它是轴对称图形 B.它是中心对称图形
C.它的外角和是360° D.它的每个内角都是140°
【正确答案】 B

7-5（提升）如图，在中，顶点，，，将与正方形ABCD组成的图形绕点O顺时针旋转，每次旋转，则第70次旋转结束时，点D的坐标为（　　）

A. B. C.） D.
【正确答案】 D

7-6（提升）如图，在平面直角坐标系中，，，，请确定一点D，使得以点A，B，C，D为顶点的四边形是轴对称图形但不是中心对称图形，则点D的坐标可能是（）

A. B. C. D.
【正确答案】 C

【原卷 8 题】知识点三角形内角和定理的应用,同弧或等弧所对的圆周角相等

【正确答案】
A
【试题解析】

8-1（基础）如图，AB是⊙O的直径，C，D是⊙O上的两点．若∠CAB=，则∠ADC的度数为（）

A. B. C. D.
【正确答案】 D

8-2（基础）如图，圆的两条弦AB，CD相交于点E，且，则的度数为（）

A.50° B.80° C.70° D.90°
【正确答案】 B

8-3（巩固）如图，线段是的直径，为上两点，如果，那么的度数是(　　)

A.15° B.30° C.45° D.60°
【正确答案】 B

8-4（巩固）如图，是的直径，是上两点，若，则的度数是（）

A. B. C. D.
【正确答案】 D

8-5（提升）如图，△ABC内接于⊙O，EF为⊙O直径，点F是BC弧的中点，若∠B＝40°，∠C＝60°，则∠AFE的度数（　　）

A.10° B.20° C.30° D.40°
【正确答案】 A

8-6（提升）如图，是半⊙的直径，点是弧的中点，D为弧BC的中点，连接，于点．则（）

A.3 B. C. D.
【正确答案】 C

【原卷 9 题】知识点分式有意义的条件

【正确答案】
x≠3
【试题解析】

9-1（基础）如果在实数范围内有意义，那么实数的取值范围是________．
【正确答案】 x≠-3

9-2（基础）若代数式有意义，则实数x的取值范围是___________．
【正确答案】

9-3（巩固）若代数式有意义，则x的取值范围是__________．
【正确答案】且

9-4（巩固）若代数式有意义，则x的取值范围是________．
【正确答案】

9-5（提升）在函数中，自变量的取值范围是___________．
【正确答案】且

9-6（提升）如果式子有意义，那么的取值范围是______．
【正确答案】且

【原卷 10 题】知识点无理数的估算

【正确答案】
2或3，答案不唯一
【试题解析】

10-1（基础）写出一个比4大且比5小的无理数：__．
【正确答案】（答案不唯一）

10-2（基础）若已知是一个无理数，且1＜＜3，请写出一个满足条件的a值 _____．
【正确答案】 2

10-3（巩固）若n为整数，且，则n的值为________________．
【正确答案】 4

10-4（巩固）写出一个比大且比小的整数是____________．
【正确答案】 2或3

10-5（提升）若的小数部分为，整数部分为，则的值为_____________．
【正确答案】

10-6（提升） 2021年5月7日，《科学》杂志发布了我国成功研制出可编程超导量子计算机“祖冲之”号的相关研究成果．祖冲之是我国南北朝时期杰出的数学家，他是第一个将圆周率精确到小数点后第七位的人，他给出的两个分数形式：（约率）和（密率）．同时期数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法，其理论依据是：设实数的不足近似值和过剩近似值分别为和（即有，其中，，，为正整数），则是的更为精确的近似值．例如：已知，则利用一次“调日法”后可得到的一个更为精确的近似分数为：；由于，再由，可以再次使用“调日法”得到的更为精确的近似分数……现已知，则使用两次“调日法”可得到的近似分数为______．
【正确答案】

【原卷 11 题】知识点综合提公因式和公式法分解因式

【正确答案】

【试题解析】

11-1（基础）分解因式：______________．
【正确答案】

11-2（基础）分解因式：4a2﹣16＝_____．
【正确答案】 4（a+2）（a-2）

11-3（巩固）分解因式___________．
【正确答案】

11-4（巩固）分解因式：__________．
【正确答案】

11-5（提升）已知，，那么______，______．
【正确答案】 -1 0

11-6（提升）在实数范围内分解因式：_____________.
【正确答案】

【原卷 12 题】知识点直角三角形的两个锐角互余,切线的性质定理,应用切线长定理求解

【正确答案】

【试题解析】

12-1（基础）如图，，，是的切线，，，为切点，如果，，则的长为__________．

【正确答案】 2

12-2（基础）如图，PA、PB是⊙O的切线，若∠APO＝25°，则∠BPA＝_____．

【正确答案】 50°

12-3（巩固）如图，PA，PB是的切线，切点分别为A，B，连接OB，AB．如果，那么∠P的度数为______．

【正确答案】 40°

12-4（巩固）把光盘、含 60°角的三角板和直尺如图摆放，AB＝2，则光盘的直径是_____．

【正确答案】

12-5（提升） PA，PB，CD是⊙O的切线，A，B，E是切点，CD分别交PA，PB于C，D两点，若∠APB=50°，则∠COD的度数为____．
【正确答案】 65°或115°

12-6（提升）如图，PA、PB是⊙O的切线，切点分别为A、B，BC是⊙O的直径，PO交⊙O于E点，连接AB交PO于F，连接CE交AB于D点．下列结论：①PA＝PB；②OP⊥AB；③CE平分∠ACB；④OF＝AC；⑤E是△PAB的内心；⑥△CDA≌△EDF．其中一定成立的是（只填序号） ________．

【正确答案】 ①②③④⑤

【原卷 13 题】知识点根据一元二次方程根的情况求参数

【正确答案】
m＞4
【试题解析】

13-1（基础）若关于的方程有两个不相等的实数根，则的取值范围是_____．
【正确答案】

13-2（基础）关于x的一元二次方程x2-2x+m=0有两个不相等的实数根．请你写出一个满足条件的m值：m=______．
【正确答案】 0

13-3（巩固）已知关于x的方程有两个相等的实数根，则m的值是_________．
【正确答案】 2或

13-4（巩固）若关于x的一元二次方程有实数根，则k的取值范围是_______．
【正确答案】且

13-5（提升）如果方程的三根可以作为一个三角形的三边之长，那么实数的取值范围是___．
【正确答案】

13-6（提升）对于实数，，定义运算“”：，关于的方程恰好有三个实数根，则的取值范围是__．
【正确答案】

【原卷 14 题】知识点一次函数与反比例函数的交点问题

【正确答案】

【试题解析】

14-1（基础）如图，双曲线与直线交于A，B两点，若点A的坐标为，则点B的坐标为__________．

【正确答案】 (-3,-4)

14-2（基础）在平面直角坐标系xOy中，直线y＝x与双曲线y＝交于点A（2，m），则k的值是 _____．
【正确答案】 4

14-3（巩固）已知直线y=kx与双曲线y=的一个交点的横坐标是2，则另一个交点坐标是_____．
【正确答案】（-2，-4）

14-4（巩固）在平面直角坐标系中，直线与双曲线交于点，若，则的值为_______．
【正确答案】 4

14-5（提升）如图，直线与双曲线交于两点，若的面积为4，则k的值为 ___________．

【正确答案】

14-6（提升）如图，过点A（4，5）分别作x轴、y轴的平行线，交直线y=-x+6于B，C两点，若函数的图象与△ABC的边有2个公共点，则k的取值范围是______．

【正确答案】 5＜k＜8或9＜k＜20

【原卷 15 题】知识点全等三角形综合问题

【正确答案】

15-1（基础）在平面直角坐标系中，将点绕原点顺时针旋转90°，所得到的对应点的坐标为__________．
【正确答案】

15-2（基础）请仔细观察用直尺和圆规作一个角等于已知角的示意图，请你根据所学的图形的全等这一章的知识，说明画出的依据是_____．（填SAS、ASA、SSS或HL）

【正确答案】

15-3（巩固）如图是5x5的正方形网络，以点D、E为两个顶点作位置不同的格点三角形，使所作的格点三角形与△ABC全等，这样的格点三角形最多可以画出_______个

【正确答案】 4

15-4（巩固）如图所示的网格是正方形网格，点A，B，C，D均落在格点上，则∠BAC+∠ACD＝_____°．

【正确答案】 90

15-5（提升）如图，在中，点D、E分别、上的点，与交于点O．给出下列三个条件：①；②；③．利用其中两个条件可以证明是等腰三角形，这两个条件可以是____________．

【正确答案】 ①③或②③

15-6（提升）如图，点E为矩形ABCD的边BC长上的一点，作DF⊥AE于点F，且满足DF＝AB．下面结论：①△DEF≌△DEC；②S△ABE＝S△ADF；③AF＝AB；④BE＝AF．其中正确的结论是_____．

【正确答案】 ①②④．

【原卷 16 题】知识点数字类规律探索,求方差,根据方差判断稳定性,运用方差做决策

【正确答案】
9，5，2，8
【试题解析】
【分析】开始数据是1，甲先填入的数据使方差最大，说明甲填入的是最大的数字9，乙填入的数据使方差最小，说明乙填入的数据是中间数字5，以此类推即可算出答案．
【详解】由题意可知，开始数字是1，
∵甲填入数字后数据方差最大，
∴甲先填入9，
又∵乙填入数字后数据方差最小，
∴乙再填入5，
又∵甲填入的数字使此时的方差最大，
∴甲填入的数字应为2，
∴最后乙填入的数字是8，
∴依次填入的数字是9，5，2，8．故9，5，2，8．
本题考查方差的概念和应用．熟练掌握方差越大，数据波动越大，方差越小，数据波动越小是解题的关键．

16-1（基础）甲、乙两台包装机同时包装糖果，分别从中随机抽取5袋，测得它们的实际质量（单位：g）如下表所示：
甲
100
102
99
101
98
乙
100
97
104
97
102
那么_________包装机包装的5袋糖果的质量比较稳定（填“甲”或“乙”）．
【正确答案】甲

16-2（基础）从四个数中任取两个不同的数（记作）构成一个数组（其中且将与视为同一个数组），若满足：对于任意的和都有则的最大值______________．
【正确答案】 5

16-3（巩固）某班甲、乙、丙三名同学20天的体温数据记录如下表：
甲的体温
乙的体温
丙的体温
温度（℃）
36.1
36.4
36.5
36.8
温度（℃）
36.1
36.4
36.5
36.8
温度（℃）
36.1
36.4
36.5
36.8
频数
5
5
5
5
频数
6
4
4
6
频数
4
6
6
4
则在这20天中，甲、乙、丙三名同学的体温情况最稳定的是________．
【正确答案】丙

16-4（巩固）从﹣1，0，2，3四个数中任取两个不同的数（记作ak，bk）构成一个数对Mk＝{ak，bk）（其中k＝1，2，…，s，且将{ak，bk}与{bk，ak}视为同一个数对），若满足：对于任意的Mi＝{ai，bi}和Mj＝{aj，bj）（i≠j，1≤i≤s，1≤j≤s）都有ai+bi≠aj+bj，则s的最大值是_____．
【正确答案】 5

16-5（提升）如图，等腰Rt△ABC中，∠ACB＝90°，AC＝BC＝1，且AC边在直线a上，将△ABC绕点A顺时针旋转到位置①可得到点P1，此时AP1＝；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2＝1+；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3＝2+；…．按此规律继续旋转，直至得到点P2020为止，则AP2020＝_____．

【正确答案】 1346+674．

16-6（提升）如图，直线与轴相交于点，过点作轴的平行线交直线于点，过点作轴的平行线交直线于点，再过点作轴的平行线交直线于点，过点及作轴的平行线交直线于点，…，依此类推，得到直线上的点，，，…，与直线上的点，，，…，则的长为______．

【正确答案】

【原卷 17 题】知识点特殊角三角函数值的混合运算

【正确答案】

【试题解析】

17-1（基础）计算：
【正确答案】 -2

17-2（基础）计算：．
【正确答案】

17-3（巩固）计算：．
【正确答案】 4

17-4（巩固）计算：．
【正确答案】

17-5（提升）计算：．
【正确答案】

17-6（提升）计算：cos230°+|1﹣|﹣2sin45°+（π﹣3.14）0
【正确答案】

【原卷 18 题】知识点求不等式组的解集

【正确答案】
−1