高中数学高考 2021届高考二轮精品专题四 平面向量（理） 学生版(1)

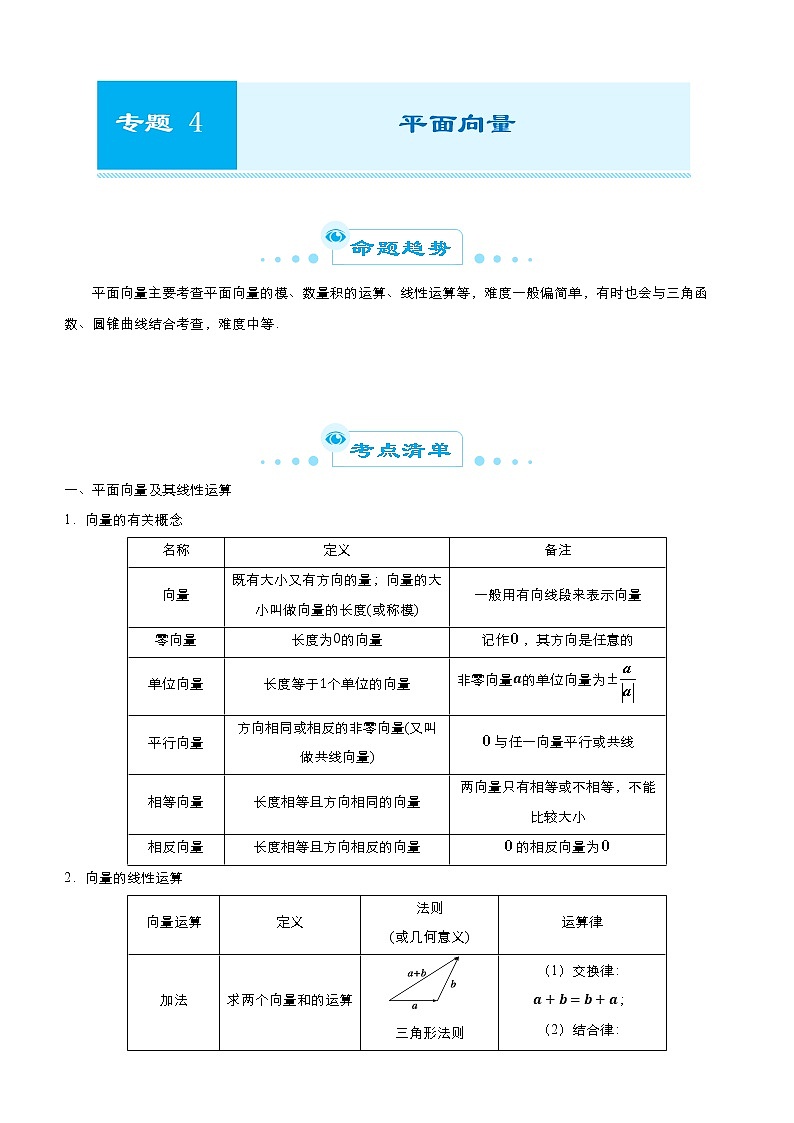
平面向量主要考查平面向量的模、数量积的运算、线性运算等，难度一般偏简单，有时也会与三角函数、圆锥曲线结合考查，难度中等．

一、平面向量及其线性运算

1．向量的有关概念

2．向量的线性运算

3．共线向量定理

向量与共线，当且仅当有唯一一个实数，使得．

二、平面向量基本定理和平面向量的坐标表示

1．平面向量基本定理

如果，是同一平面内的两个不共线的非零向量，那么对于这一平面内的任一向量，有且只有一对实数，，使．

其中，不共线的非零向量，叫做表示这一平面内所有向量的一组基底．

2．平面向量的坐标运算

向量加法、减法、数乘向量及向量的模

设，，则，，

，．

3．平面向量共线的坐标表示

设，，其中．

．

三、平面向量的数量积

1．定义：已知两个非零向量和，它们的夹角为，则数量叫做向量和的数量积，

记作．

规定：零向量与任一向量的数量积为．

2．投影：叫做向量在方向上的投影．

3．数量积的坐标运算：设向量，，则

（1）

（2）

（3）

四、平面向量的相关结论

1．“三点”共线的充要条件：为平面上一点，则三点共线的充要条件是 (其中）．

2．三角形中线向量公式：若为的边的中点，则．

一、选择题．

1．已知平面向量满足，则向量的夹角为（    ）

A． B．             C．-----D．

2．在等腰梯形ABCD中，AB=2CD，若，，则（    ）

A． B．        C．--------D．

3．若平面向量与b的夹角为，，，则（    ）

A． B．             C．18----D．12

4．已知向量，，，若，则（    ）

A． B．             C．-----D．

5．若向量，，则的面积为（    ）

A． B．            C．------D．

6．已知为等边三角形，，设点，满足，，与交于点，则（    ）

A． B．              C．1----D．2

7．若向量，满足，，则在方向上的投影为（    ）

A．1 B．             C．-----D．

8．已知向量，为平面内的单位向量，且，向量与共线，则的最小值为（    ）

A．1 B．              C．-----D．

9．如图，延长正方形ABCD的边CD至点E，使得DE=CD，动点P从点A出发，沿正方形的边按逆时针方向运动一周后回到点A，若，则下列判断正确的是（    ）

A．满足的点P必为BC的中点     B．满足的点P有且只有一个

C．满足的点P有且只有一个       D．的点P有且只有一个

10．在中，点是的中点，，线段与交于点，动点在内部活动（不含边界），且，其中、，则的取值范围是（    ）

A． B．         C．-------D．

二、填空题．

11．已如，且，则的最大值为__________．

12．如图梯形，且，，在线段上，，则的最小值为_______．

13．已知向量的模长为1，平面向量满足：，则的取值范围是_________．

14．已知，，是平面向量，且，是互相垂直的单位向量，若对任意均有的最小值为，则的最小值为___________．

三、解答题．

15．已知向量，，函数．

（1）若，求函数的最值；

（2）若，且，，求的值．

一、解答题．

1．已知，，向量与向量的夹角为，设向量，向量．

（1）求的值；

（2）设，求的表达式；若与的夹角为锐角，求实数的取值范围．

一、选择题．

1．如图所示的中，点是线段上靠近的三等分点，点是线段的中点，则（    ）

A． B．   C．----------D．

2．如图，四边形是边长为的正方形，，点为内（含边界）的动点，设，则的最大值是（    ）

A． B．           C．------D．

3．如图，B是的中点，，P是平行四边形内（含边界）的一点，且，则下列结论正确的个数为（    ）

①当时，；

②当P是线段的中点时，，；

③若为定值1，则在平面直角坐标系中，点P的轨迹是一条线段；

④的最大值为．

A．1 B．2              C．3---D．4

二、填空题．

4．已知，，，则向量与的夹角的正切值为_________．

5．已知单位向量，满足：，则向量与向量的夹角___________．

6．已知向量，若，且，则的最大值为______．

7．如图，在直角梯形中，已知，，，对角线交于点，点在上，且满足，则的值为___________．

8．已知平面内非零向量a，，，满足，，，若，则的取值范围是______．

9．已知，，分别为的三个内角，，的对边，，且，为的重心，则________．

一、选择题．

1．【答案】D

【解析】，即，

．

，，故选D．

【点评】本题考查了向量的数量积，向量的夹角，以及向量垂直的条件，属于基础题．

2．【答案】A

【解析】解法一：如图，取的中点，连结，因为四边形为等腰梯形，，

所以，所以四边形为平行四边形，

所以，故选A．

解法二：如图，取的中点，连结，

因为四边形为等腰梯形，，所以，

所以四边形为平行四边形，所以，故选A．

【点评】在几何图形中进行向量运算：

（1）构造向量加、减法的三角形法则和平行四边形法则；

（2）树立“基底”意识，利用基向量进行线性运算．

3．【答案】B

【解析】，，故选B．

【点评】本题主要考了向量的运算以及向量的模长，属于基础题．

4．【答案】B

【解析】由题设可得，

因为，故，解得，

所以，故，故选B．

【点评】本题考了向量的坐标运算以及向量的垂直的条件，模长的计算，属于基础题．

5．【答案】A

【解析】因为，，

所以，，，

则，，所以，故选A．

【点评】本题考点为向量夹角的计算，以及三角形面积的计算，属于基础题．

6．【答案】D

【解析】因为，所以，

所以，所以为的一个靠近的三等分点，

又因为，所以为的中点，

过作交于点，如下图所示：

因为且，所以，所以，

所以，

所以，故选D．

【点评】解答本题的关键是确定点的位置，通过将待求的向量都转化为，

即可直接根据数量积的计算公式完成求解．

7．【答案】B

【解析】设，的夹角为，

则，

则，即在方向上的投影为，故选B．

【点评】本题考查了向量数量积的运算，向量投影的计算公式，考查了计算能力，属于基础题．

8．【答案】D

【解析】因为向量与共线，所以存在唯一的实数，使得，

所以，

所以，

又向量，为平面内的单位向量，所以，，

又，所以，

所以，所以的最小值为，故选D．

【点评】本题主要考查共线定理的应用及平面向量数量积，关键是根据共线，利用共线定理将用向量，表示，再通过平方转化为二次函数最值问题．

9．【答案】C

【解析】如图建系，取，

∵，

∴，

动点从点出发，沿正方形的边按逆时针方向运动一周回到点，

当时，有且，∴，∴，

当时，有且，则，∴，∴，

当时，有且，则，∴，∴，

当时，有且，则，∴，∴，

综上，．

选项A，取，满足，此时，因此点不一定是的中点，

故A错误；

选项B，当点取点或的中点时，均满足，此时点不唯一，故B错误；

选项C，当点取点时，且，解得，为，故C正确；

选项D，当点取的中点或的中点时，均满足，此时点不唯一，故D错误，

故选C．

【点评】求解本题的关键在于根据题中所给条件，利用建系的方法，讨论的位置，根据，确定的范围，即可求解．（向量用坐标表示后，向量的计算和证明都归结为数的运算，这使问题大大简化）

10．【答案】D

【解析】如下图所示，连接并延长交于点，

设，，则，，

，

，

又，，，

，

，，则，

即，即，

因此，的取值范围是，故选D．

【点评】本题考查利用平面向量的基本定理求与参数有关的代数式的取值范围，解题的关键在于引入参数表示、，并结合不等式的基本性质求出的取值范围．

二、填空题．

11．【答案】

【解析】因为，，且，

所以，

因为，所以与的夹角为，即，

因为，所以，即点D是以AC为直径的圆上的点，

以B为原点，BC为x轴正方向建系，如图所示：

所以，，，

设以AC为直径的圆的圆心为P，所以，且，

所以D的轨迹的方程为，

的最大值为，

故答案为．

【点评】解题的关键是根据题意，分析可得D点的轨迹为圆，进而求得圆的方程，根据圆的几何性质求解，考查分析理解，数形结合的能力，属中档题．

12．【答案】

【解析】因为，所以向量与的夹角和向量与的夹角相等，

设向量与的夹角为，

因为，所以，

即，

整理得，解得，，

如图，过点作垂线，垂足为，建立如图所示的直角坐标系，

易知，，，，

则，，，

，，，

，

因为，所以当时，取最小值，最小值为，

故答案为．

【点评】本题考查向量的数量积的求法，可通过建立直角坐标系的方式进行求解，考查向量的运算法则，

考查向量的数量积的坐标表示，考查计算能力，考查转化与化归思想，是难题．

13．【答案】

【解析】由题意知：不妨设，，

则根据条件可得，，

根据柯西不等式得，

因为，

，，

当且仅当时取等号；

令，则，

又，则，

所以，当时，，即；

，而，所以当时，，即，

故的取值范围是．

【点评】设，，则根据条件可得：，

，利用柯西不等式和换元法把问题转化为求二次函数的最值问题是解决本题的关键．

14．【答案】

【解析】，

即，所以，

即，

设为轴的方向向量，为轴方向向量，所以，对应的坐标为，

所以，得，

，

因为为抛物线向上平移个单位，

所以焦点坐标为，准线为，所以点到的距离与到的距离相等，

，

当且仅当时，取最小值．

故答案为．

【点评】关于向量模长的问题，一般没有坐标时，利用平方公式展开计算；有坐标时，代入坐标公式求解，

涉及模长的最值问题，一般需要转化为点与点之间的距离，或者点到线的距离等问题，利用几何方法求解．

三、解答题．

15．【答案】（1）最大值为，最小值为；（2）．

【解析】（1）因为，，

所以，

因为，所以，

所以当，即时，最小，最小值为0，此时最大，最大值为；

所以当，即时，最大，最大值为1，此时最小，最小值为．

即的最大值为，最小值为．

（2）由（1）得，

又，所以，所以，

因为，所以，所以．

因为，，所以，

所以

．

【点评】本题主要考查数量积的坐标表示，三角函数在闭区间上的最值求法，以及两角和的余弦公式的应用，意在考查学生的数学运算能力和转化能力，属于基础题．解题关键是：整体思想的应用，一是将看成整体，利用三角函数图象求出最值；二是将看成整体，利用两角和的余弦公式展开求出．

一、解答题．

1．【答案】（1）1；（2），或且．

【解析】（1）．

（2）

，

因为与的夹角为锐角，所以，

即，解得或．

又由和共线，解得，

所以实数的取值范围是或且．

【点评】本题考查向量的数量积．向量夹角为锐角是的充分不必要条件，夹角为0（即同向时）也有，同样向量夹角为钝角是的充分不必要条件．

一、选择题．

1．【答案】B

【解析】依题意，，故选B．

【点评】本题主要考了向量的线性运算，属于基础题．

2．【答案】D

【解析】以为原点，为轴建立如图所示的平面直角坐标系：

因为四边形是边长为的正方形，，

所以，，，，，

所以，

设，则，所以，

所以，即求的最大值，

因为点为内（含边界）的动点，

所以由图可知，平移直线到经过点时，取得最大值，

所以的最大值是，故选D．

【点评】建立平面直角坐标系，转化为线性规划求解是解题关键．

3．【答案】C

【解析】当时，，则在线段上，故，故①错；

当是线段的中点时，

，故②对；

为定值1时，，，三点共线，又是平行四边形内（含边界）的一点，故的轨迹是线段，

故③对；

如图，过作，交于，作，交的延长线于，

则：，

又；，；

由图形看出，当与重合时：；

此时取最大值0，取最小值1；所以取最大值，故④正确，

所以选项②③④正确，故选C．

【点评】若，则三点共线．

二、填空题．

4．【答案】

【解析】设向量与的夹角为，因为，所以，

又因为，，所以，即，

又，所以，即有，

所以向量与的夹角的正切值为，故答案为．

【点评】本题考查了利用向量的数量积求夹角的应用问题，属于基础题．

5．【答案】

【解析】因为单位向量，，，

所以，即，

，所以．

故答案为．

【点评】本题考查了向量垂直的条件，以及向量夹角的计算，属于基础题．

6．【答案】

【解析】∵，且，∴与的夹角为，

设，则，

∵，∴，

又，∴，化简得，

∴，当且仅当时，等号成立，

∴，故答案为．

【点评】本题考查了平面向量的混合运算，还涉及利用基本不等式解决最值问题，考查学生的逻辑推理能力，属于中档题．

7．【答案】

【解析】如图以为坐标原点，所在直线为轴，所在直线为轴建立平面直角坐标系，

则，，，，则，

因为，所以，

所以是的一个三等分点，且，所以．

设，则，

因为，所以，解得，

则，

所以，故答案为．

【点评】本题考查向量的数量积的应用，考查向量的坐标表示，考查计算能力．

8．【答案】

【解析】，，，，

又，a，的夹角为，

建立如图所示直角坐标系，

设，，，则，，

设，

，，

则点C在以为圆心，1为半径的圆上，

的取值范围转化为圆上的点到定点的距离的范围，

圆心到点的距离为，

的取值范围为，故答案为．

【点评】本题考查了向量垂直与数量积的关系，向量的坐标运算，考查了数形结合的思想方法以及圆上的点到定点距离的最大最小值，属于中档题．

9．【答案】

【解析】由余弦定理得，∴，

∵，，

将代入得，

所以，

设以为邻边的平行四边形的另一个顶点为，则，

，

故答案为．

【点评】本题考查余弦定理在解三角形中的应用，要熟练使用上弦定理角化边，并结合向量的数量积运算可更快的求解．

江西多宝格教育咨询有限公司（旗下网站：好教育http：//www．jtyhjy．com）郑重发表如下声明：

    一、本网站的原创内容，由本公司依照运营规划，安排专项经费，组织名校名师创作，经由好教育团队严格审核通校，按设计版式统一精细排版，并进行版权登记，本公司拥有著作权；

    二、本网站刊登的课件、教案、学案、试卷等内容，经著作权人授权，本公司享有独家信息网络传播权；

    三、任何个人、企事业单位（含教育网站）或者其他组织，未经本公司许可，不得以复制、发行、表演、广播、信息网络传播、改编、汇编、翻译等任何方式使用本网站任何作品及作品的组成部分；

    四、一旦发现侵犯本网站作品著作权的行为，欢迎予以举报（举报电话：0791-83857059），举报内容对查实侵权行为确有帮助的，一经确认，将给予奖励；

    五、我们将联合全国各地文化执法机关和相关司法机构，并结合广大用户和网友的举报，严肃清理侵权盗版行为，依法追究侵权者的民事、行政和刑事责任！

特此声明

江西多宝格教育咨询有限公司