专题 临界（极值）问题(课件)-高中物理课件（人教版必修第一册）

这是一份人教版 (2019)必修 第一册全册综合优秀课件ppt，共32页。PPT课件主要包含了临界问题，实例分析，典例分析，常见临界条件归纳，非标准解法，标准解法等内容，欢迎下载使用。

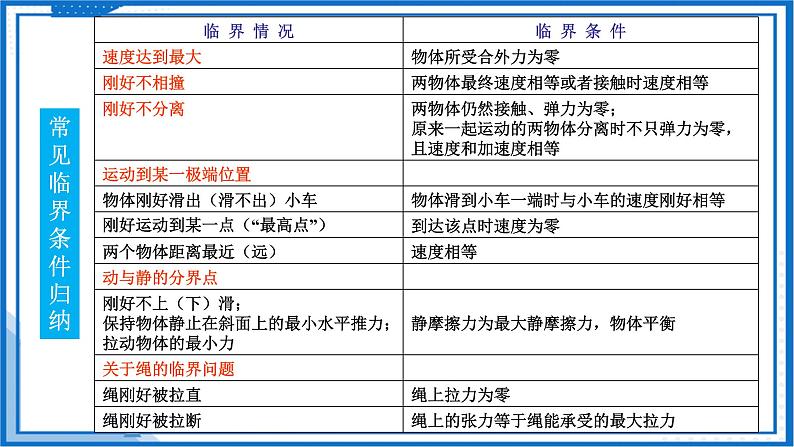
摩擦力是被动力，由物体间的相对运动趋势决定。①静摩擦力为零是运动趋势方向发生变化的临界状态。②静摩擦力最大是物体恰好保持相对静止的临界状态。（存在静摩擦的连接系统，当系统外力大于最大静摩擦力时，物体间不一定有相对滑动，相对滑动与相对静止的临界条件是静摩擦力达最大值）
2、临界问题的常见类型及临界条件
(1)弹力发生突变的临界条件（比如：绳子或者接触面）
弹力发生在两物体的接触面之间，是一种被动力，其大小由物体所处的运动状态决定。相互接触的两个物体将要脱离的临界条件是弹力为零。
(2)摩擦力发生突变的临界条件
1、动力学中临界问题的特征
在动力学问题中出现某种物理现象(或物理状态)刚好要发生或刚好不发生的转折状态即为临界问题。问题中出现“最大”“最小”“刚好”“恰能”等关键词语，一般都会涉及临界问题，隐含相应的临界条件。（涉及临界状态的问题叫做临界问题）
3、求解临界极值问题的三种常用方法
（1）认真审题，仔细分析研究对象所经历的变化的物理过程，找出临界状态。（2）寻找变化过程中相应物理量的变化规律，找出临界条件。（3）以临界条件为突破口，列临界方程，求解问题。
解决临界问题的基本思路
【例题】在水平向右运动的小车上，有一倾角θ=370的光滑斜面，质量为m的小球被平行于斜面的细绳系住而静止于斜面上，如图所示。当小车分别以a1=g和a2=2g 的加速度水平向右运动时，绳对小球的拉力及斜面对小球的弹力各为多大？
易见 ：支持力FN 随加速度a 的增大而减小 当a=gctθ= 4g/3 时，支持力FN =0 小球即将脱离斜面
则沿x轴方向 FTcsθ-FNsinθ=ma沿y轴方向 FTsinθ+FNcsθ=mg
取小球为研究对象并受力分析，建立正交坐标系
将 a1=g 、a2=2g 分别代入得a1=g时：FT=7mg/5 ；FN=mg/5 a2=2g时：FT= 11mg/5 ；FN=-2mg/5
解：小球即将脱离斜面支持力FN =0
对小球进行受力分析，得合力：
F=mgctθ =ma
a=gctθ= 4g/3
因为a1=g＜ 4g/3，所以斜面对小球有弹力
则沿x轴方向 FTcsθ-FNsinθ=ma 沿y轴方向 FTsinθ+FNcsθ=mg
解得：FT=7mg/5 ；FN=mg/5
【小结】相互接触的两个物体将要脱离的临界条件是相互作用的弹力刚好为零。
因为a2=2g ＞ 4g/3，所以小球已经脱离（飘离）斜面
故斜面对小球有弹力FN=0
【拓展】上述问题中，若小车向左加速运动 ，试求加速度a=g时的绳中张力。
则沿x轴方向 FNsinθ - FTcsθ =ma 沿y轴方向 FNcsθ + FTsinθ=mg
FT的负号表示绳已松弛，故FT=0
【小结】绳子松弛的临界条件是：绳中拉力刚好为零。
解：绳子即将变柔软时拉力FT =0
F=mgtanθ =ma
a=gtanθ= 3g/4
因为a=g ＞ 3g/4，故绳已松弛
绳上拉力为零FT =0
【例题】A、B两个滑块靠在一起放在光滑水平 面上，其质量分别为2m和m,从t=0时刻起，水平力F1和F2同时分别作用在滑块A和B上，如图所示。已知F1=（10+4t）N, F2=(40-4t)N,两力作用在同一直线上，求滑块开始滑动后，经过多长时间A、B发生分离？
解 ：由题意分析可得两物体分离的临界条件是：两物体之间刚好无相互作用的弹力，且此时两物体仍具有相同的加速度。分别以A、B为研究对象，水平方向受力分析如图
由牛顿第二定律得 F1=ma F2=2ma
即(40-4t) =2(10+4t）解得 t=5/3 (s)
【例题】有一质量M=4kg的小车置于光滑水平桌面上，在小车上放一质量m=6kg的物块，动摩擦因素µ=0.2,现对物块施加F=25N的水平拉力,如图所示，求小车的加速度？（设车与物块之间的最大静摩擦力等于滑动摩擦力且g取10m/s2)
再取整体为研究对象受力如图
而 F=25N 得：Fm=(M+m) am=30N
故系统的加速度 a=F/(M+m)=2.5 m/s2
【小结】存在静摩擦的连接系统，当系统外力大于最大静摩 擦力时，物体间不一定有相对滑动。 相对滑动与相对静止的临界条件是：静摩擦力达最大值
则两者保持相对静止的最大加速度为 am=fm/M= µmg/M=3m/s2
解：当木块与小车之间的摩擦力达最大静摩擦力时，对小车水平方向受力分析如图
【例题】如图所示，质量均为M的两个木块A、B在水平力F的作用下，一起沿光滑的水平面运动，A与B的接触面光滑，且与水平面的夹角为60°，求使A与B一起运动时的水平力F的范围。
分析：当水平推力F很小时，A与B一起作匀加速运动，当F较大时，B对A的弹力竖直向上的分力等于A的重力时，地面对A的支持力为零，此后，物体A将会相对B滑动。显而易见，本题的临界条件就是水平力F为某一值时，恰好使A沿AB面向上滑动，即物体A对地面的压力恰好为零.
解：当水平力F为某一值时，恰好使A沿AB面向上滑动，即物体A对地面的压力恰好为零，受力分析如图对整体： ①隔离A： ② ③ ④联立上式解得： ∴ 水平力F的范围是：0＜F≤
【例题】如图所示， 细线的一端固定在倾角为45°的光滑楔形滑块A的顶端P处，细线的另一端拴一质量为m的小球(重力加速度为g)。(1)当滑块至少以多大的加速度向右运动时，细线对小球的拉力刚好等于零？(2)当滑块至少以多大的加速度向左运动时，小球对滑块的压力等于零？
(1)当FT＝0时，小球受重力mg和斜面支持力FN作用，如图甲所示，则FNcs 45°＝mg，FNsin 45°＝ma，解得a＝g。故当滑块向右运动的加速度为g时，细线的拉力为0。
【例题】如图所示， 细线的一端固定在倾角为45°的光滑楔形滑块A的顶端P处，细线的另一端拴一质量为m的小球(重力加速度为g)。(1)当滑块至少以多大的加速度向右运动时，细线对小球的拉力刚好等于零？(2)当滑块至少以多大的加速度向左运动时，小球对滑块的压力等于零？(3)当滑块以a′＝2g的加速度向左运动时，细线中的拉力为多大？
【例题4】如图所示，物体A的质量为M＝1 kg，静止在光滑水平面上的平板车B的质量为m＝0.5 kg、长为L＝1 m．某时刻A以v0＝4 m/s水平向右的初速度滑上平板车B的上表面，在A滑上B的同时，给B施加一个水平向右的拉力．忽略物体A的大小，已知A与B之间的动摩擦因数为μ＝0.2，取重力加速度g＝10 m/s2.试求：如果要使A不至于从B上滑落，拉力F应满足的条件．
拉力F＝maB－μMg＝1 N．若F<1 N，则A滑到B的右端时，速度仍大于B的速度，于是将从B上滑落，所以F必须大于或等于1 N．当F较大时，在A到达B的右端之前，就与B具有相同的速度，之后A必须相对于B静止，才不会从B的左端滑落．对A、B整体和A分别应用牛顿第二定律得F＝(m＋M)a，μMg＝Ma 解得F＝3 N．若F大于3 N，A就会相对于B向左滑下综合得出力F应满足的条件是1 N≤F≤3 N．
【例题】如图甲所示，物体P置于光滑的水平面上，用轻细线跨过质量不计的光滑定滑轮连接一个重力G＝10 N的重物Q，物体P向右运动的加速度为a1；若细线下端不挂重物，而用F＝10 N的力竖直向下拉细线下端，如图乙所示，这时物体P的加速度为a2，则 (　　)A.a1＜a2　　B.a1＝a2C.a1＞a2 D.条件不足，无法判断
解：设系统的加速度大小为a，绳1的张力大小为F1，绳2的张力大小为F2。对C由牛顿第二定律得F1－μmCg＝mCa，对A、C整体由牛顿第二定律得F2－μ(mA＋mC)g＝(mA＋mC)a，对B由牛顿第二定律得mBg－F2＝mBa，解得：a＝3.75 m/s2，F1＝6.25 N，F2＝18.75 N。
【例题】如图所示，A、B、C三个物体以轻质细绳1、2相连，mA＝2 kg，mB＝3 kg，mC＝1 kg，A、C与水平桌面间的动摩擦因数μ＝0.25，不计绳2与滑轮间的摩擦，取g＝10 m/s2，求：(1)系统的加速度大小；(2)绳1和绳2中的张力大小。
【例题】如图所示，矩形盒内用两根细线固定一个质量为m＝1.0 kg 的均匀小球，a线与水平方向成53°角，b线水平。两根细线所能承受的最大拉力都是Fm＝15 N。(cs 53°＝0.6，sin 53°＝0.8，g取10 m/s2)求：(1)当该系统沿竖直方向匀加速上升时，为保证细线不被拉断，加速度可取的最大值。(2)当该系统沿水平方向向右匀加速运动时，为保证细线不被拉断，加速度可取的最大值。
解:(1)竖直向上匀加速运动时小球受力如图所示，当a线拉力为15 N时，由牛顿第二定律得：竖直方向有：Fmsin 53°－mg＝ma，水平方向有：Fmcs 53°＝Fb，解得Fb＝9 N，此时加速度有最大值a＝2 m/s2。(2)水平向右匀加速运动时，由牛顿第二定律得：竖直方向有：Fasin 53°＝mg，水平方向有：Fb－Facs 53°＝ma，解得Fa＝12.5 N，当Fb＝15 N时，加速度最大，有a＝7.5 m/s2。
【例题】如图所示，在倾角为θ的光滑斜面上端固定一劲度系数为k的轻弹簧，弹簧下端连有一质量为m的小球，小球被一垂直于斜面的挡板A挡住，此时弹簧没有形变。若手持挡板A以加速度a(a【例题】一个物体沿摩擦因数一定的斜面加速下滑，下列图象，哪个比较准确地描述了加速度a与斜面倾角θ的关系（ ）
解：设摩擦因数为μ，则a=gSinθ-μgCsθ 做如下几种假设： 当θ=00时，物体静止在水平面上，a=0 当θ=arctgμ时，物体开始匀速下滑，a=0 当θ>arctgμ时，物体加速下滑，a>0 当θ=900时，F=μmgCs900=0，加速度达到极限 值，a=g即物体做自由落体运动。 综上假设，不难判断出“D”答案是合理的。
【例题】如图示，质量为M=2Kg的木块与水平地面的动摩擦因数μ=0.4，木块用轻绳绕过光滑的定滑轮，轻绳另一端施一大小为20N的恒力F，使木块沿地面向右做直线运动，定滑轮离地面的高度h=10cm，木块M可视为质点，问木块从较远处向右运动到离定滑轮多远时加速度最大？最大加速度为多少？
解：设当轻绳与水平方向成角θ时，对M有 Fcsθ-μ(Mg-Fsinθ)=Ma 整理得： F(csθ＋μsinθ)-μMg=Ma 令 (csθ＋μsinθ)=A ，可知，当A取最大值时a最大。利用三角函数知识有：