2022-2023学年湖南省郴州市第一中学北校区高二上学期期末数学试题含解析

2022-2023学年湖南省郴州市第一中学北校区高二上学期期末数学试题

一、单选题

1．经过点且倾斜角为的直线的方程是（    ）

A． B．

C． D．

【答案】B

【分析】首先求出直线的斜率，再利用点斜式求出直线方程；

【详解】由倾斜角为知，直线的斜率，

因此，其直线方程为，即

故选：B

2．若向量与向量互相垂直，则的值为（       ）

A．1 B．2 C．3 D．4

【答案】C

【分析】由，知，得到关于的方程，解方程即可得解.

【详解】因为向量与向量互相垂直

，即，解得：

故选：C

3．记等差数列的前n项和为，已知，，则（    ）

A．2 B．1 C．0 D．

【答案】D

【分析】利用题给条件列出关于首项公差d的方程组，解之即可求得的值.

【详解】设等差数列的首项为，公差为d，

则，解之得

故选：D

4．如图，在直三棱柱中，是等边三角形，，，，分别是棱，，的中点，则异面直线与所成角的余弦值是（    ）

A． B． C． D．

【答案】A

【分析】建立空间直角坐标系，利用向量法求得异面直线与所成角的余弦值.

【详解】设分别是的中点，连接，则，

由于是等边三角形，所以，

根据直三棱柱的性质可知，平面平面，且交线为，

平面，所以平面，

由于平面，所以.

根据根据直三棱柱的性质可知，平面，所以平面，

平面，所以，

由此以为原点，建立空间直角坐标系如下图所示，

设，

则，

所以，

设异面直线与所成角为，

则.

故选：A

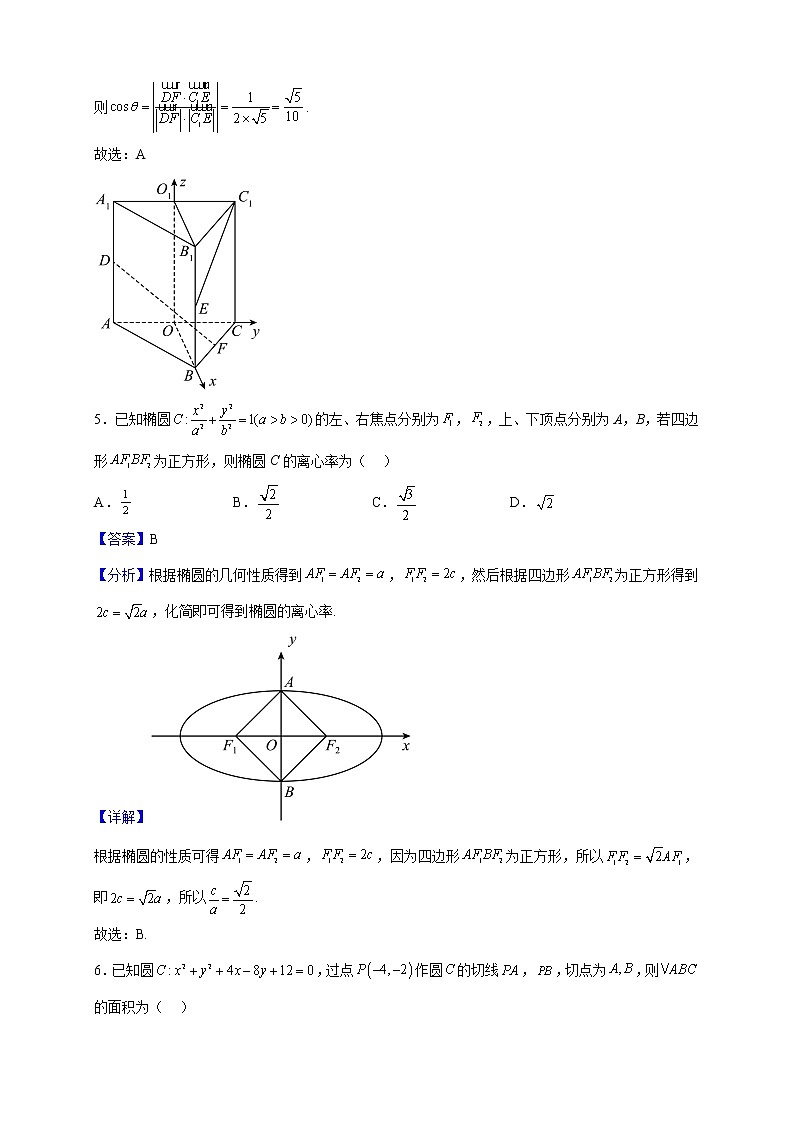
5．已知椭圆的左、右焦点分别为，，上、下顶点分别为A，B，若四边形为正方形，则椭圆C的离心率为（    ）

A． B． C． D．

【答案】B

【分析】根据椭圆的几何性质得到，，然后根据四边形为正方形得到，化简即可得到椭圆的离心率.

【详解】

根据椭圆的性质可得，，因为四边形为正方形，所以，即，所以.

故选：B.

6．已知圆，过点作圆的切线，，切点为，则的面积为（    ）

A． B． C． D．

【答案】C

【分析】设与交于点，根据切线的性质及勾股定理求得，再根据等面积法求出，再利用勾股定理求出，从而可得出答案.

【详解】解：设与交于点，

则且为的中点，

圆，化为，

则圆心，半径，，

则，

由，

得，

所以，

所以.

故选：C.

7．已知定义域为的函数满足以下条件：

①；

②;

③.

则成立的的取值范围是（    ）

A． B．

C． D．

【答案】D

【分析】由题意可得是上的单调递增奇函数，且有，分，分别求解，再取并集即可得答案.

【详解】解：，

是定义在上的奇函数，

；

在单调递增，则在单调递增，又，

，

当或时，；当或时，．

不等式，转化为或，即或，

解得或，

故成立的的取值范围是.

故选：

8．城市的许多街道是互相垂直或平行的，因此往往不能沿直线行走到达目的地，只能按直角拐弯的方式行走.如果按照街道的垂直和平行方向建立平面直角坐标系，对两点，定义两点间“距离”为，则平面内与轴上两个不同的定点的“距离”之和等于定值（大于）的点的轨迹可以是（    ）

A． B．

C． D．

【答案】A

【分析】分横坐标在、之外（内）的区域两种情况讨论，结合所给距离公式判断即可.

【详解】解：根据题意，横坐标在、之外的区域，不能出现与轴垂直的线段，

否则该线段上的点与、的“距离”之和不会是定值；

横坐标在、之内的区域，则必须与轴平行，否则该线段上的点与、的“距离”之和不会是定值.

故选：A.

二、多选题

9．过抛物线的焦点作轴的垂线，交抛物线于，两点，为抛物线的顶点，则下列说法正确的是（    ）

A．点坐标为 B．准线方程为

C． D．

【答案】ACD

【分析】根据抛物线的定义求焦点，准线方程，通径AB的长度，最后可求.

【详解】抛物线的焦点为，准线方程为，

当时，，

∴，.

故选：ACD.

10．已知定义域为的函数，则（    ）

A．为奇函数 B．为偶函数

C．在上单调递减 D．在上单调递增

【答案】AB

【分析】由定义判断AB；由导数得出单调性判断C；由特殊值判断D.

【详解】，则为奇函数；，，则为偶函数；当时，，即在上单调递增；，，，即在上不是单调递增，故只有AB正确；

故选：AB

11．已知数列中，，，则关于数列的说法正确的是（    ）

A．

B．数列为递增数列

C．

D．数列的前n项和小于

【答案】BCD

【分析】根据递推关系求得数列的通项公式，从而对选项ABC一一判断即可；利用裂项相消法求数列的前n项和，即可判断D.

【详解】由，

得，即，又，

所以是以2为首项，1为公差的等差数列，

所以，即，

所以，故A错误，C正确；

，所以为递增数列，故B正确；

，

所以数列的前n项和为

，故D正确.

故选：BCD．

12．如图，在直三棱柱中，，，为的中点，过的截面与棱，分别交于点F，G（G，E，F可能共线），则下列说法中正确的是（    ）

A．存在点F，使得

B．线段长度的取值范围是

C．四棱锥的体积为2时，点F只能与点B重合

D．设截面，，的面积分别为，，，则的最小值为4

【答案】BCD

【分析】以点为坐标原点，、、所在直线分别为、、轴建立空间直角坐标系，设点、，其中，，利用空间向量垂直的坐标表示可判断A选项；求出与的关系式，利用反比例函数的基本性质可判断B选项；利用等积法可判断C选项；利用基本不等式可判断D选项.

【详解】因为平面，，以点为坐标原点，、、所在直线分别为、、轴建立如下图所示的空间直角坐标系，

则、、、、、、，设点、，其中，.

对于A选项，若存在点，使得，且，，

，解得，不合乎题意，A错；

对于B选项，设，其中、，

即，即，可得，

，则，所以，，B对；

对于C选项，，

其中，故，

又，故

即，故点F只能与点B重合，C对；

对于D选项，，，

则点到直线的距离为，

，则点到直线的距离为

，

所以，，故，

，当且仅当时，等号成立，故的最小值为，D对.

故选：BCD.

【点睛】关键点睛：建立空间直角坐标系，运用空间向量的性质是解题的关键.

三、填空题

13．在等比数列中，，是方程的两个实数根，则的值为________

【答案】

【分析】根据等比数列的性质，结合已知条件，即可直接求解.

【详解】设等比数列的公比为，因为是方程的两个实数根，

所以＝＝2，，

所以，，则，所以．

故答案为：.

14．曲线在点处的切线平行于直线，则点的坐标为______．

【答案】或

【分析】求导得到，解得或，得到坐标.

【详解】由已知得，令，则，解得或，

所以或．经检验，点与均符合题意．

故答案为：或

15．已知双曲线方程为，焦距为8，左､右焦点分别为，，点A的坐标为，P为双曲线右支上一动点，则的最小值为___________.

【答案】

【分析】由焦距为8，求得，即可得双曲线方程，进而可得，结合图形，只有当三点共线时，取最小值为，求出即得答案.

【详解】解：如图所示，

由双曲线为等轴双曲线，且焦距为8，

所以，，

即，，

所以双曲线的方程为：，

所以，，，

由双曲线定义得，

所以

，

当三点共线时，最小为

故.

故答案为：.

四、双空题

16．中国古代数学名著《九章算术》中将底面为矩形且有一条侧棱垂直于底面的四棱锥称为“阳马”.现有一“阳马”的底面是边长为3的正方形，垂直于底面的侧棱长为4，则该“阳马”的外接球表面积为__________，内切球的球心和外接球的球心之间的距离为__________.

【答案】          ##

【分析】由条件求出四棱锥的表面积和体积根据内切球的性质确定内切球的半径，再确定外接球的球心及半径，由此计算外接球的表面积和球心的距离.

【详解】如图，为正方形，所以，

设垂直于平面，平面，所以，又，平面，所以平面，平面，所以，故为直角三角形，同理可得为直角三角形，，

由题，，所以，

四棱锥表面积，体积，

设内切球半径为r，则，得.

以，，分别为x，y，z轴建立如图空间直角坐标系，

因为内切球半径，所以内切球球心，

记的中点为，则，所以为四棱锥外接球的球心，又，，所以外接球球心，半径，外接球表面，

两点间距离.

故答案为：；.

五、解答题

17．在△ABC中，已知M（1，6）是BC边上一点，边AB，AC所在直线的方程分别为．

（1）若，求直线BC的方程；

（2）若，求直线BC的横截距．

【答案】（1）；（2）

【分析】（1）求出，根据垂直关系，利用点斜式求解方程；

（2）建立方程求出，得出直线BC的方程即可得解.

【详解】（1）由题边AB，AC所在直线的方程分别为．

的交点就是，

若，，

所以直线BC的方程：即；

（2）设，

所以解得，

所以

所以直线的方程为，即，

令得，

直线BC的横截距.

18．如图在四棱锥中，底面，且底面是平行四边形.已知是中点.

(1)求证：平面平面；

(2)求平面与平面所成锐二面角的余弦值.

【答案】(1)证明见解析

(2)

【分析】（1）先证明出平面，利用面面垂直的判定定理即可证明；（2）以A为原点，分别为x，y，z轴正方向建系，利用向量法求解.

【详解】（1）面，且，

.

∵是中点,所以.

同理可证：.

又面，面，,

平面.

∵面，

∴平面平面.

（2），.

以A为原点，分别为x，y，z轴正方向建系，如图：

则.

设平面的法向量

则，得，不妨取，则.

由（1）得是平面的一个法向量，

所以，

所以平面与平面所成锐二面角的余弦值为.

19．已知等差数列的公差为，前n项和为，其中，，成等比数列，.

(1)求的通项公式；

(2)若，且，设数列的前n项和，求证.

【答案】(1)

(2)证明见解析

【分析】（1）根据，，成等比数列，代入求和公式即可求得首项和公差，即可求得通项公式；

（2）根据求得，然后求得数列的通项后利用裂项求和即可证明.

【详解】（1）解：因为，，成等比数列，则，即

又，则，由得，即

则有可得，

所以.

（2）证明：由，且

所以当时，则有

又也满足，故对任意的，有，

则

所以

由于单调递增，所以．

综上：.

【点睛】.

20．已知函数.

(1)当时，讨论函数的单调性；

(2)当时，恒成立，求a的取值范围.

【答案】(1)在上单调递减，在上单调递增

(2)

【分析】（1）利用导数即可求得函数的单调性；

（2）先将不等式恒成立，转化为不等式恒成立，进而求得a的取值范围.

【详解】（1）时，，，

在定义域上单调递增，且，

则当时，；当时，，

∴在上单调递减，在上单调递增.

（2）当时，恒成立，即恒成立，

∴恒成立，令， 则；

又在上单调递减，所以，

所以.

21．如图，在平面直角坐标系xOy中，已知圆及点.

(1)若直线过点，与圆相交于两点，且，求直线l的方程；

(2)圆上是否存在点，使得成立？若存在，求点的个数；若不存在，请说明理由.

【答案】(1)或

(2)存在，两个

【分析】(1)根据垂径定理可得圆心到直线的距离为1，然后利用点到直线的距离即可求解；

(2) 假设圆上存在点，设，则，利用题干条件得到点也满足，根据两圆的位置关系即可得出结果.

【详解】（1）圆可化为，圆心为，

若的斜率不存在时，，此时符合要求.  

当的斜率存在时，设的斜率为，则令，

因为，由垂径定理可得，圆心到直线的距离

，                       

所以直线的方程为或.

（2）假设圆上存在点，设，则，

，  

即，即，             

，                 

与相交，则点有两个.

22．已知双曲线的焦点到渐近线的距离为2，渐近线的斜率为2．

(1)求双曲线的方程；

(2)设过点的直线与曲线交于两点，问在轴上是否存在定点，使得为常数？若存在，求出点的坐标及此常数的值；若不存在，说明理由．

【答案】(1)；

(2)答案见解析.

【分析】（1）根据已知可求出，，即可求出双曲线的方程；

（2）设，，.设出直线方程，与双曲线方程联立得到，根据韦达定理求出，用点的坐标表示出，整理得到，因为该式为常数，所以有，求出，代入即可求出常数.

【详解】（1）由已知可得，双曲线的渐近线方程为，双曲线焦点，.

则到渐近线，即的距离为，所以，

又渐近线的斜率为2，即，所以，

所以双曲线的方程为.

（2）由已知可得，直线的斜率存在，设斜率为，则.

联立直线的方程与双曲线的方程可得，，

设，，.

当，即时，此时直线与双曲线的渐近线平行，不满足题意，所以，.

，解得，且.

由韦达定理可得，，且，.

又，，

则，

因为，，

所以，

要使为常数，则应与无关，

即应有，解得，此时是个常数，这样的点存在.

所以，在轴上存在定点的坐标为，使得为常数.