

2023年华东师大版数学八年级下册《矩形、菱形与正方形》单元质量检测(含答案)
展开《矩形、菱形与正方形》单元质量检测
一 、选择题
1.矩形的对角线一定具有的性质是( )
A.互相垂直 B.互相垂直且相等 C.相等 D.互相垂直平分
2.如图,将矩形ABCD沿AE折叠,若∠BAD′=30°,则∠AED′等于( )
A.30° B.45° C.60° D.75°
3.菱形不具备的性质是( )
A.是轴对称图形 B.是中心对称图形
C.对角线互相垂直 D.对角线一定相等
4.已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形面积是( )
A.16 B.16 C.8 D.8
5.如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
A.2对 B.3对 C.4对 D.5对
6.如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形,且它的一条直角边等于斜边的一半.这样的图形有( )
A.4个 B.3个 C.2个 D.1个
7.如图,在▱ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE、CF,则四边形AECF是 ( )
A.平行四边形 B.矩形 C.菱形 D.正方形
8.在四边形ABCD中,AC与BD相交于点O,且OA=OC,OB=OD.如果再增加条件AC=BD,此四边形一定是( )
A.正方形 B.矩形 C.菱形 D.都有可能
9.若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是( )
A.矩形 B.菱形
C.对角线互相垂直的四边形 D.对角线相等的四边形
10.如图,在菱形ABCD中,AB=13,对角线AC=10,若过点A作AE⊥BC,垂足为E,则AE的长为( )
A.8 B. C. D.
11.如图,在矩形ABCD中,AB=8.将矩形的一角折叠,使点B落在边AD上的B´点处,若AB/=4,则折痕EF的长度为( )
A.8 B.4 C.5 D.10
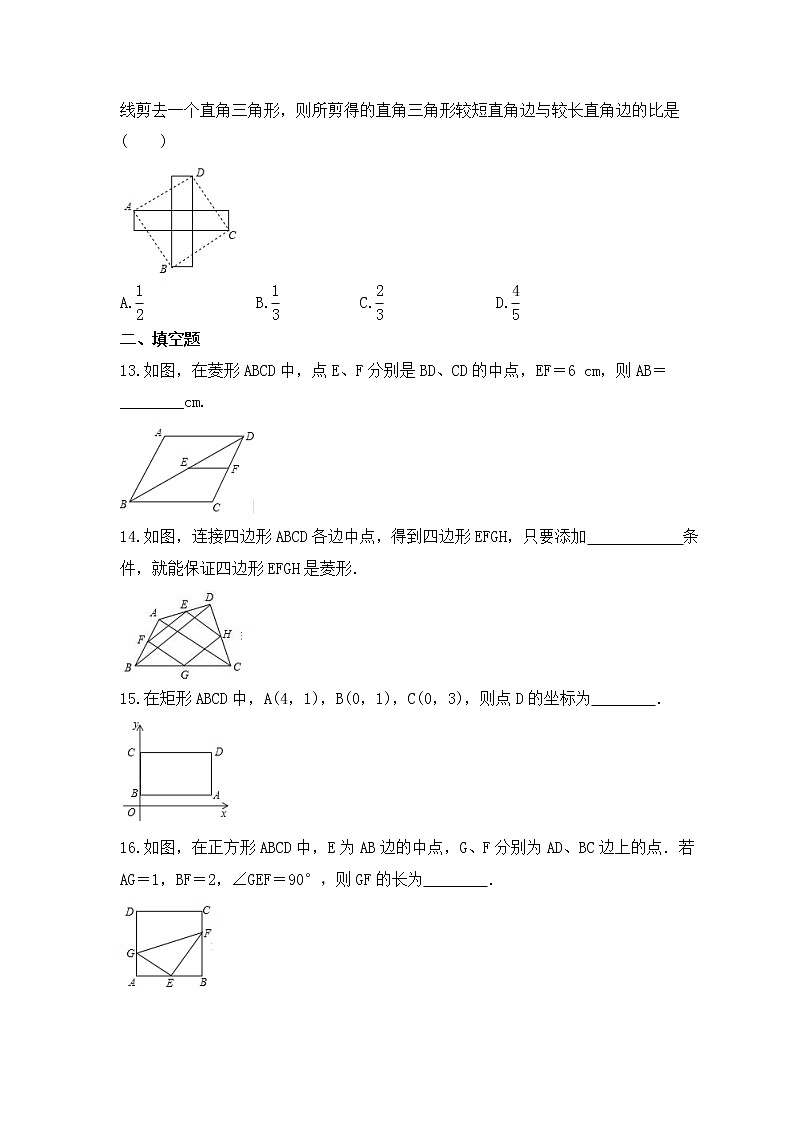
12.已知一个无盖长方体的底面是边长为1的正方形,侧面是长为2的长方形,现展开铺平.如图,依次连结点A,B,C,D得到一个正方形,将周围的四个长方形沿虚线剪去一个直角三角形,则所剪得的直角三角形较短直角边与较长直角边的比是( )
A. B. C. D.
二 、填空题
13.如图,在菱形ABCD中,点E、F分别是BD、CD的中点,EF=6 cm,则AB=________cm.
14.如图,连接四边形ABCD各边中点,得到四边形EFGH,只要添加 条件,就能保证四边形EFGH是菱形.
15.在矩形ABCD中,A(4,1),B(0,1),C(0,3),则点D的坐标为 .
16.如图,在正方形ABCD中,E为AB边的中点,G、F分别为AD、BC边上的点.若AG=1,BF=2,∠GEF=90°,则GF的长为 .
17.如图,矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为 .
18.如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;则S3﹣S2= .
三 、作图题
19.有5个边长为1的正方形,排列形式如图:请把它们分割后拼接成一个大正方形.
① 大正方形的边长为 .
②画出分割线及拼接图.
四 、解答题
20.如图,在矩形ABCD中,AD=12,AB=7,DF平分∠ADC,AF⊥EF.
(1)求证:AF=EF;
(2)求EF长.
21.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且AC=2DE,连接AE交OD于点F,连接CE、OE.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
22.如图,已知在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.
23.如图,在▱ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:▱ABCD是菱形;
(2)若AB=5,AC=6,求▱ABCD的面积.
24.将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F.
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形的边长;
(3)在(2)的条件下折痕EF的长.
25.如图1,在矩形纸片ABCD中,AB=12 cm,AD=20 cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P,Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P,Q分别在边BA,BC上移动,求出点E在边AD上移动的最大距离.
图1 图2
答案
1.C.
2.C
3.D.
4.C
5.C
6.C.
7.C
8.B.
9.C.
10.C.
11.C.
12.C.
13.答案为:12.
14.答案为:AC=BD.
15.答案为:(4,3).
16.答案为:3.
17.答案为:10.
18.答案为:.
19.解:①大正方形的边长为:.
②如图所示:
20.证明:(1)∵四边形ABCD是矩形,
∴∠B=∠C=∠ADC=90°,AB=DC=7,BC=AD=12,
∴∠BAF+∠AFB=90°,
∵DF平分∠ADC,
∴∠ADF=∠CDF=45°,
∴△DCF是等腰直角三角形,
∴FC=DC=7,
∴AB=FC,
∵AF⊥EF,
∴∠AFE=90°,
∴∠AFB+∠EFC=90°,
∴∠BAF=∠EFC,
在△ABF和△FCE中,
∠BAF=∠EFC;AB=FC;∠B=∠C,
∴△ABF≌△FCE(ASA),
∴EF=AF;
(2)解:BF=BC﹣FC=12﹣7=5,
在Rt△ABF中,由勾股定理得:
AF==,则EF=AF=.
21.证明:(1)四边形ABCD是菱形,
∴OA=OC=AC,AD=CD,
∵DE∥AC且DE=AC,
∴DE=OA=OC,
∴四边形OADE、四边形OCED都是平行四边形,
∴OE=AD,
∴OE=CD;
(2)解:∵AC⊥BD,
∴四边形OCED是矩形,
∵在菱形ABCD中,∠ABC=60°,
∴AC=AB=2,
∴在矩形OCED中,CE=OD=.
∴在Rt△ACE中,AE=.
22.证明:(1)∵正方形ABCD
∴AD=BA,∠BAD=90°,即∠BAQ+∠DAP=90°
∵DP⊥AQ
∴∠ADP+∠DAP=90°
∴∠BAQ=∠ADP
∵AQ⊥BE于点Q,DP⊥AQ于点P
∴∠AQB=∠DPA=90°
∴△AQB≌△DPA(AAS)
∴AP=BQ
(2)①AQ﹣AP=PQ
②AQ﹣BQ=PQ
③DP﹣AP=PQ
④DP﹣BQ=PQ
23.(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D.
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°.
又∵BE=DF,
∴△AEB≌△AFD,
∴AB=AD,
∴▱ABCD是菱形;
(2)连接BD交AC于O.
∵四边形ABCD是菱形,AC=6,
∴AC⊥BD,OA=OC=AC=×6=3.
∵AB=5,
∴OB===4,
∴BD=2OB=8,
∴S▱ABCD=×AC×BD=24.
24.证明:(1)∵矩形ABCD折叠使A,C重合,折痕为EF,
∴OA=OC,EF⊥AC,EA=EC,
∵AD∥AC,
∴∠FAC=∠ECA,
在△AOF和△COE中,
∴△AOF≌△COE,
∴OF=OE,
∵OA=OC,AC⊥EF,
∴四边形AECF为菱形;
(2)①设菱形的边长为x,则BE=BC﹣CE=8﹣x,AE=x,
在Rt△ABE中,∵BE2+AB2=AE2,
∴(8﹣x)2+42=x2,解得x=5,
即菱形的边长为5;
②在Rt△ABC中,AC=4,
∴OA=AC=2,
在Rt△AOE中,AE=,OE=,
∴EF=2OE=2.
25.(1)证明:∵折叠纸片使B点落在边AD上的E处,折痕为PQ,
∴点B与点E关于PQ对称,
∴PB=PE,BF=EF,∠BPF=∠EPF.
又∵EF∥AB,
∴∠BPF=∠EFP,∴∠EPF=∠EFP,
∴EP=EF,∴BP=BF=EF=EP,
∴四边形BFEP为菱形.
(2)解:①∵四边形ABCD是矩形,
∴BC=AD=20,CD=AB=12,∠A=∠D=90°.
∵点B与点E关于PQ对称,
∴CE=BC=20.
在Rt△CDE中,DE==16,
∴AE=AD-DE=20-16=4.
在Rt△APE中,AE=4,AP=12-PB=12-PE,
∴EP2=42+(12-EP)2.
解得EP=,
∴菱形BFEP的边长为 cm.
②当点Q与点C重合时,点E离点A最近,由①知,此时AE=4.
当点P与点A重合时,如图,
点E离点A最远,此时四边形ABQE为正方形,AE=AB=12,
∴点E在边AD上移动的最大距离为8 cm.









