广东省惠州市惠阳区沙田中学2022-2023学年八年级下学期3月月考数学试题(含答案)

这是一份广东省惠州市惠阳区沙田中学2022-2023学年八年级下学期3月月考数学试题(含答案)，共11页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
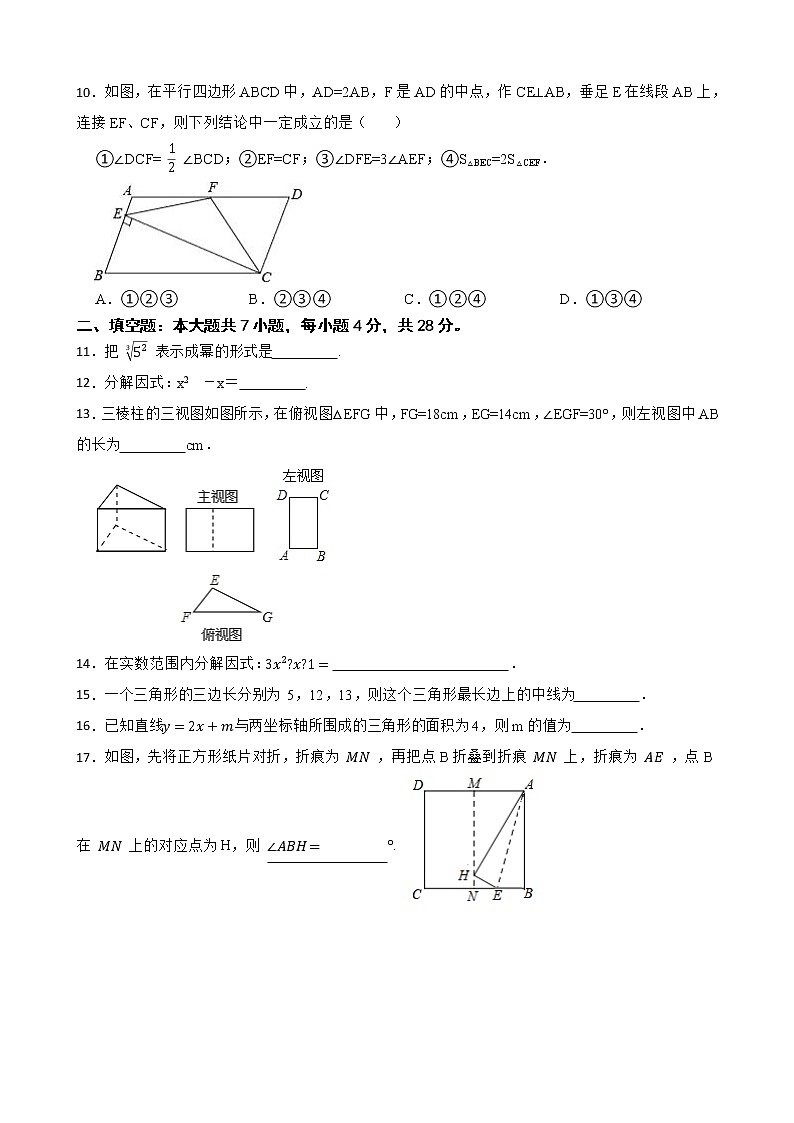
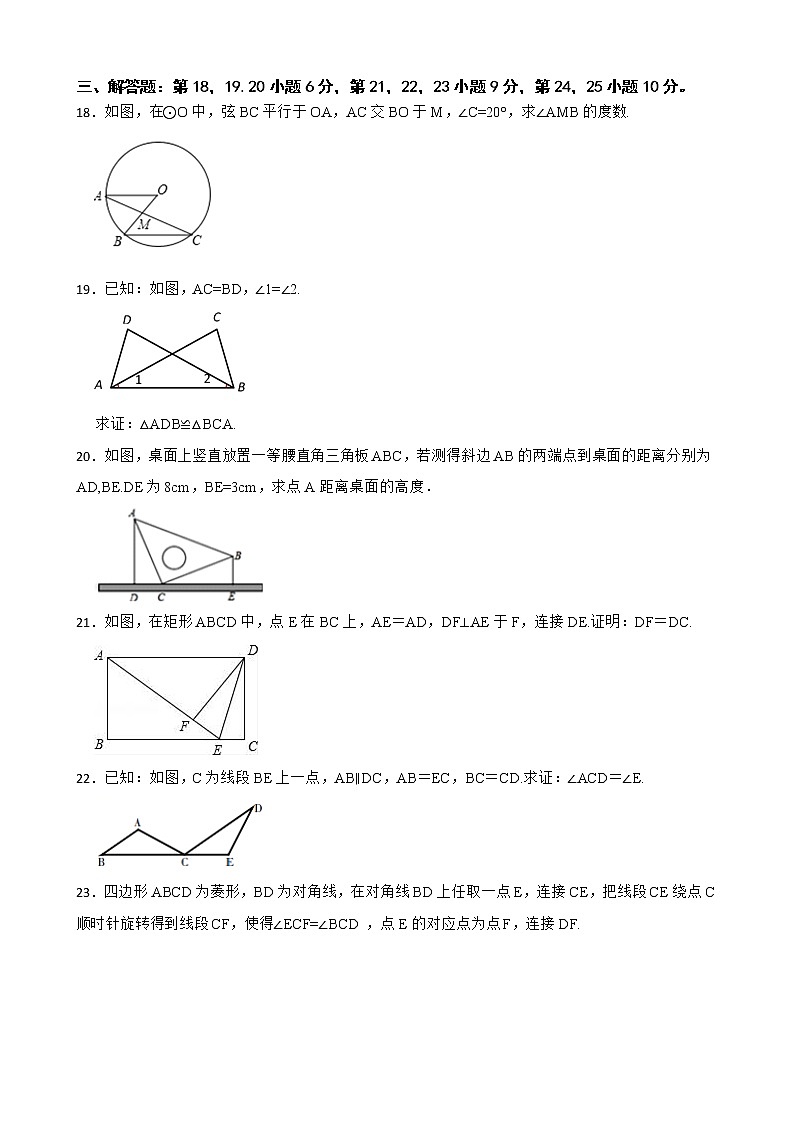
 2022-2023学年度第二学期惠州市惠阳区沙田中学八年级数学开学测试题一、单选题：本大题共10小题，每小题3分，共30分。1．以下列各组长度的线段为边，能构成三角形的是（　　）A．7，3，4 B．5，6，12 C．3，4，5 D．1，2，32．要使分式 有意义，则x的取值范围是（　　）A． B． C． D．3．下列运算结果等于a6的是（　　）   A． B． C． D．4．下列图形中，不是轴对称图形的是（　　）  A． B． C． D．5．如图，AD＝AE，补充下列一个条件后，仍不能判定△ABE≌△ACD的是（　　）  A．∠B＝∠C B．AB＝ACC．∠AEB＝∠ADC D．BE＝CD6．下列因式分解正确的是（　　）A． B．C． D．7．计算的结果是（　　）A． B．C． D．8．下列代数式中：，，，共有分式（　　）A．2个 B．3个 C．4个 D．5个9．一个凸多边形的内角和与外角和之比为2：1，则这个多边形的边数为（　　）A．5 B．6 C．7 D．810．如图，在平行四边形ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是（　　）①∠DCF= ∠BCD；②EF=CF；③∠DFE=3∠AEF；④S△BEC=2S△CEF．A．①②③ B．②③④ C．①②④ D．①③④二、填空题：本大题共7小题，每小题4分，共28分。11．把 表示成幂的形式是　     　.12．分解因式：x2－x＝　     　.13．三棱柱的三视图如图所示，在俯视图△EFG中，FG=18cm，EG=14cm，∠EGF=30°，则左视图中AB的长为　     　cm．14．在实数范围内分解因式：　                    　．  15．一个三角形的三边长分别为 5，12，13，则这个三角形最长边上的中线为　     　．16．已知直线与两坐标轴所围成的三角形的面积为4，则m的值为　     　．17．如图，先将正方形纸片对折，折痕为 ，再把点B折叠到折痕 上，折痕为 ，点B在 上的对应点为H，则 　     　°.    三、解答题：第18，19.20小题6分，第21，22，23小题9分，第24，25小题10分。18．如图，在⊙O中，弦BC平行于OA，AC交BO于M，∠C=20°，求∠AMB的度数.19．已知：如图，AC=BD，∠1=∠2.求证：△ADB≌△BCA.20．如图，桌面上竖直放置一等腰直角三角板ABC，若测得斜边AB的两端点到桌面的距离分别为AD,BE.DE为8cm，BE=3cm，求点A距离桌面的高度．21．如图，在矩形ABCD中，点E在BC上，AE＝AD，DF⊥AE于F，连接DE.证明：DF＝DC.22．已知：如图，C为线段BE上一点，AB∥DC，AB＝EC，BC＝CD.求证：∠ACD＝∠E.23．四边形ABCD为菱形，BD为对角线，在对角线BD上任取一点E，连接CE，把线段CE绕点C顺时针旋转得到线段CF，使得∠ECF=∠BCD ，点E的对应点为点F，连接DF.（1）如图1，求证：BE=DF；（2）如图2，若DF= CF=10， ∠DFC=2∠BDC，求菱形ABCD的边长.24．如图所示， 中，∠BAC=90°，∠C=30°，BC=2，⊙O是△ABC的外接圆，D是CB延长线上一点，且BD=1，连接DA，点P是射线DA上的动点。（1）求证DA是⊙O的切线；（2）DP的长度为多少时，∠BPC的度数最大，最大度数是多少？请说明理由。（3）点P运动的过程中，（PB+PC）的值能否达到最小，若能，求出这个最小值，若不能，说明理由.25．定义：只有一组对角是直角的四边形叫做损矩形，连接它的两个非直角顶点的线段叫做这个损矩形的直径．（1）如图1，损矩形ABCD，∠ABC=∠ADC=90°，则该损矩形的直径是线段　     　．（2）在线段AC上确定一点P，使损矩形的四个顶点都在以P为圆心的同一圆上（即损矩形的四个顶点在同一个圆上），请作出这个圆，并说明你的理由．友情提醒：“尺规作图”不要求写作法，但要保留作图痕迹．（3）如图2，△ABC中，∠ABC=90°，以AC为一边向形外作菱形ACEF，D为菱形ACEF的中心，连接BD，当BD平分∠ABC时，判断四边形ACEF为何种特殊的四边形？请说明理由．若此时AB=3，BD= ，求BC的长．
答案解析部分1．【答案】C2．【答案】A3．【答案】D4．【答案】A5．【答案】D6．【答案】D7．【答案】C8．【答案】B9．【答案】B10．【答案】A11．【答案】12．【答案】x(x-1)13．【答案】714．【答案】15．【答案】16．【答案】17．【答案】7518．【答案】解：∵∠C=20°  ∴∠AOB=40°又∵弦BC∥半径OA∴∠OAC=∠C=20°∵∠AMB是△AOM的外角∴∠AMB=60°.19．【答案】证明：在△ADB和△BCA中，  ∵AC=BD，∠1=∠2，AB=BA，∴△ADB≌△BCA(SAS).20．【答案】解：∵∠ADC=∠BEC=∠ACB=90°，  ∴∠ACD+∠BCE=90°，∠ACD+∠DAC=90°，∴∠DAC=∠BCE，在△ACD和△CBE中， ，∴△ADC≌△CEB，∴DC=BE=3cm，AD=CE，∵DE=8cm，∴AD=5cm21．【答案】证明：∵DF⊥AE于F，  ∴∠DFE＝90°在矩形ABCD中，∠C＝90°∴∠DFE＝∠C 在矩形ABCD中，AD∥BC∴∠ADE＝∠DEC   ∵AE＝AD，∴∠ADE＝∠AED ∴∠AED＝∠DEC又∵DE=DE，∴△DFEC≌△DCE ∴DF＝DC22．【答案】证明：∵AB∥DC， ∴∠B＝∠ECD，∠A＝∠ACD. 在△ABC和△ECD中，∴△ABC≌△ECD（SAS）.∴∠A＝∠E.∴∠ACD＝∠E.23．【答案】（1）解：因为∠ECF=∠BCD，所以∠ECF－∠ECD=∠BCD－∠ECD，所以∠ECB=∠DCF，由旋转可得： EC=FC，因为菱形ABCD，所以BC=CD，在△BCE和△DCF中， ，所以△BCE≌△DCF，所以BE=DF，（2）解：因为DF= CF=10，所以DF=10，CF=4， 因为∠DFC=2∠BDC，所以 ∠BEF=2∠BDC，又因为∠BEF=∠BDC+∠ECD，所以∠BDC=∠ECD，所以BE=CE=CF=4，所以BD=14，因为△BCD和△CED是等腰三角形，且∠BDC是公共角所以△BCD∽△CED，所以 ，即 ，解得CD= ，所以菱形的边长为 .24．【答案】（1）证明：连接AO，易知：△ABO是等边三角形，AB=BD=1；∴∠ADC=∠DAC=∠ABO=30°，而∠AOD=60°；∴∠DAO=90°∴DA是⊙o的切线；（2）解：当点P运动到A处时，即DP=DA=时，∠BPC的度数达到最大，最大值为90°.理由如下：若点P不在A处时，不妨设点P在DA的延长线上，连接BP，与⊙o交于一点，记为点E，连接CE，∴∠BPC＜∠BEC=∠BAC=90°；（3）解：作点C关于射线DA的对称点C′，则BP+PC=BP+PC′，当点C′，P，B三点共线时，（PB+PC）的值达到最小，最小为BC.过点作DC的垂线，垂足记为点H，连接DC′；在Rt△DCP中，∠PDC=30°；∴△DCC′为等边三角形，∴H为DC的中点，∴BH=DH-DB=CD-DB=-1=；∴C′H=DH=；由勾股定理求出：BC′=；∴（PB+PC）的最小值为；25．【答案】（1）AC（2）解：作图如图：∵点P为AC中点，∴PA=PC= AC．∵∠ABC=∠ADC=90°，∴BP=DP= AC，∴PA=PB=PC=PD，∴点A、B、C、D在以P为圆心， AC为半径的同一个圆上（3）解：∵菱形ACEF，∴∠ADC=90°，AE=2AD，CF=2CD，∴四边形ABCD为损矩形，∴由（2）可知，点A、B、C、D在同一个圆上．∵BD平分∠ABC，∴∠ABD=∠CBD=45°，∴ ，∴AD=CD，∴四边形ACEF为正方形．∵BD平分∠ABC，BD= ，∴点D到AB、BC的距离h为4，∴S△ABD= AB×h=2AB=6，S△ABC= AB×BC= BC，S△BDC= BC×h=2BC，S△ACD= S正方形ACEF= AC2= （BC2+9），∵S四边形ABCD=S△ABC+S△ADC=S△ABD+S△BCD∴ BC+ （BC2+9）=6+2BC∴BC=5或BC=﹣3（舍去），∴BC=5．