2023年安徽省滁州市定远县郭集学校中考数学一模试卷(含答案)

这是一份2023年安徽省滁州市定远县郭集学校中考数学一模试卷(含答案)，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2023年安徽省滁州市定远县郭集学校中考数学一模试卷
一、选择题（本大题共10小题，共40分。在每小题列出的选项中，选出符合题目的一项）
1．（4分）﹣|2022|的相反数是（　　）
A． B．2022 C．﹣2022 D．
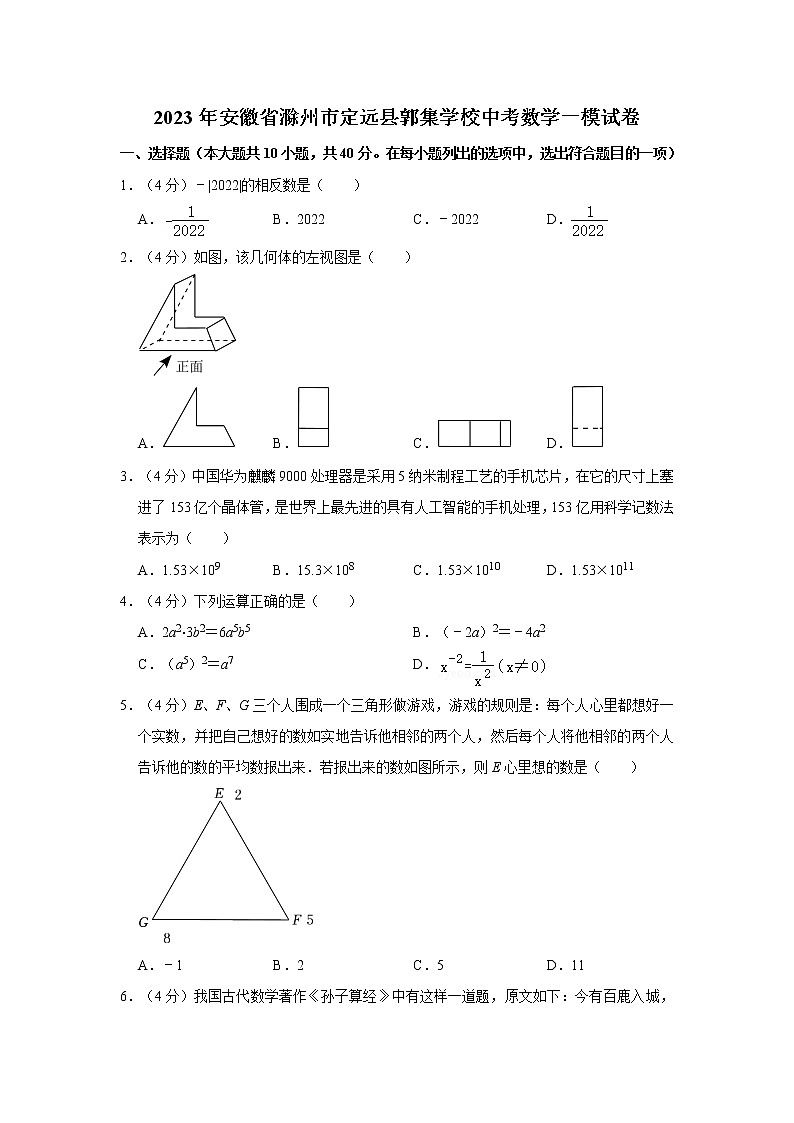
2．（4分）如图，该几何体的左视图是（　　）

A． B． C． D．
3．（4分）中国华为麒麟9000处理器是采用5纳米制程工艺的手机芯片，在它的尺寸上塞进了153亿个晶体管，是世界上最先进的具有人工智能的手机处理，153亿用科学记数法表示为（　　）
A．1.53×109 B．15.3×108 C．1.53×1010 D．1.53×1011
4．（4分）下列运算正确的是（　　）
A．2a2⋅3b2＝6a5b5 B．（﹣2a）2＝﹣4a2
C．（a5）2＝a7 D．
5．（4分）E、F、G三个人围成一个三角形做游戏，游戏的规则是：每个人心里都想好一个实数，并把自己想好的数如实地告诉他相邻的两个人，然后每个人将他相邻的两个人告诉他的数的平均数报出来．若报出来的数如图所示，则E心里想的数是（　　）

A．﹣1 B．2 C．5 D．11
6．（4分）我国古代数学著作《孙子算经》中有这样一道题，原文如下：今有百鹿入城，家取一鹿，不尽，又三家共一鹿，适尽，问：城中家几何？大意为：今有100头鹿进城，每家取一头鹿，没有取完，剩下的鹿每3家共取一头，恰好取完，问：城中有多少户人家？在这个问题中，城中人家的户数为（　　）
A．25 B．75 C．81 D．90
7．（4分）在反比例函数（k为常数）上有三点A（x1，y1），B（x2，y2），C（x3，y3），若x1＜0＜x2＜x3，则y1，y2，y3的大小关系为（　　）
A．y1＜y2＜y3 B．y2＜y1＜y3 C．y1＜y3＜y2 D．y3＜y2＜y1
8．（4分）如图所示，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，且AB＝8，MN＝3，则AC的长是（　　）

A．12 B．14 C．16 D．18
9．（4分）如图，△ABC的三个顶点的坐标分别为A（﹣6，10），B（﹣6，0），C（4，0），将△ABC绕点B顺时针旋转一定角度后使A落在y轴上，与此同时顶点C恰好落在双曲线的图象上，则该反比例函数表达式为（　　）

A． B． C． D．
10．（4分）如图，抛物线y＝x2﹣4x+3与x轴交于A，B两点，将抛物线向上平移m个单位长度后，点A，B在新抛物线上的对应点分别为点C，D，若图中阴影部分的面积为6，则平移后新抛物线的解析式为（　　）

A．y＝x2﹣4x+3 B．y＝x2﹣4x+5 C．y＝x2﹣4x+6 D．y＝x2﹣4x+7
二、填空题（本大题共4小题，共20分）
11．（5分）已知三条线段a、b、c，其中a＝1cm，b＝4cm，c是a、b的比例中项，则c＝　 　cm．
12．（5分）如图①，等边△ABC中，点P为AB边上的任意一点，且∠CPD＝60°，PD交AC于点D．设AP＝x，AD＝y．如图②是y关于x的函数图象，则图象顶点的坐标为 　 　．

13．（5分）如图，半径为4的⊙O中，CD为直径，弦AB⊥CD且过半径OD的中点，点E为⊙O上一动点，CF⊥AE于点F．当点E从点B出发顺时针运动到点D时，点F所经过的路径长为 　 　．

14．（5分）如图，若二次函数y＝ax2+bx+c（a≠0）的图象的对称轴为直线x＝1，与y轴交于点C，与x轴交于点A、点B（﹣1，0），则下列结论：①abc＞0；②二次函数的最大值为a+b+c；③a﹣b+c＜0；④b2﹣4ac＜0；⑤当y＞0时，﹣1＜x＜3．⑥3a+c＝0；其中正确的结论有 　 　．

三、解答题（本大题共9小题，共90分。解答应写出文字说明，证明过程或演算步骤）
15．（8分）先化简，再求值：÷（1+x+），其中x＝tan60°﹣tan45°．
16．（8分）如图，平面直角坐标系中，△ABC三个顶点的坐标分别为A（﹣3，5），B（﹣5，3），C（﹣2，2），将△ABC按照某种方式平移得到△A1B1C1，其中点A的对应点A1的坐标为（3，3）．

（1）请在图中画出△A1B1C1；
（2）若将△ABC到△A1B1C1的过程看成两步平移，则可将这一平移过程描述为：先向右平移 　 　个单位长度，再 　 　．
（3）已知△A1B1C1与△A2B2C2关于原点O中心对称，请在图中画出△A2B2C2，此时△A2B2C2与△ABC关于某点中心对称这一点的坐标为 　 　．
17．（8分）如图，在△ABC中，∠B＝90°，AB＝16cm，BC＝12cm，P、Q是△ABC边上的两个动点，其中点P从点A出发，沿A→B方向运动，速度为每秒2cm；点Q从点B出发，沿B→C→A方向运动，速度为每秒4cm；两点同时开始运动，设运动时间为t秒．
（1）①Rt△ABC斜边AC上的高为 　 　；
②当t＝3时，PQ的长为 　 　；
（2）当点Q在边BC上运动时，出发几秒钟后，△BPQ是等腰三角形？
（3）当点Q在边AC上运动时，直接写出所有能使△BCQ成为等腰三角形的t的值．

18．（8分）如图，小明在M处用高1米（DM＝1米）的测角仪测得旗杆AB的顶端B的仰角为30°，再向旗杆方向前进10米到F处，又测得旗杆顶端B的仰角为60°，请求出旗杆AB的高．

19．（10分）2021年，“碳中和，碳达峰”成为高频热词，为了解学生对“碳中和、碳达峰”知识的知晓情况，某校团委随机对该校九年级部分学生进行了问卷调查，调查结果共分成四个类别：A表示“从未听说过”，B表示“不太了解”，C表示“比较了解”，D表示“非常了解”．根据调查统计结果，绘制成两种不完整的统计图，请结合统计图，回答下列问题：

（1）参加这次调查的学生总人数为 　 　人；
（2）扇形统计图中，B，C部分扇形所对应的圆心角分别是 　 　，　 　；
（3）将条形统计图补充完整；
（4）在D类的学生中，有2名男生和2名女生，现需从这4名学生中随机抽取2名“碳中和、碳达峰”知识的义务宣讲员，请利用画树状图或列表的方法，求所抽取的2名学生恰好是1名男生和1名女生的概率．
20．（10分）如图，在菱形ABCD中，AD∥x轴，点A的坐标为（0，3），点B的坐标为（4，0）．CD边所在直线y1＝mx+n与x轴交于点C，与双曲线y2＝（x＜0）交于点D．
（1）求直线CD对应的函数解析式及k的值．
（2）当x＜0时，使y1﹣y2≤0的自变量x的取值范围为 　 　．

21．（12分）如图①，在等边三角形ABC中，点D在BC边上，点E在AC的延长线上，DA＝DE．

（1）求证：∠BAD＝∠EDC；
（2）如图②，M是点E关于直线BC的对称点，连接DM，AM，CM，求证：DM＝AM．

22．（12分）平安路上，多“盔”有你，在“交通安全宣传月”期间，某商店销售一批头盔，进价为每顶40元，售价为每顶68元，平均每周可售出100顶．商店计划将头盔降价销售，每顶售价不高于58元，经调查发现：每降价2元，平均每周可多售出40顶．
（1）若该商店希望平均每周获利4000元，则每顶头盔应降价多少？
（2）商店降价销售后，决定每销售1顶头盔就向某慈善机构捐赠m元（m为整数，且1≤m≤5），帮助做“交通安全”宣传．捐赠后发现，该商店每周销售这种商品的利润仍随售价的增大而增大，求m的值．
23．（14分）如图，在四边形OABC中，OA＝OC，∠OAB＝∠OCB＝90°，∠AOC＝120°．过点O作∠DOE＝60°，两边OD，OE分别与边BC，AB所在直线相交于点D，E，连接DE．
（1）AB与BC的数量关系是 　 　．
（2）如图1，当点D，E分别在边BC，AB上时，可得出结论AE+CD＝DE，请证明这个结论．（提示：将△AOE绕点O逆时针旋转120°）
（3）如图2，当点D，E分别在边BC，AB的延长线上时，（2）中的结论还成立吗？若成立，请说明理由；若不成立，请直接写出线段AE，CD，DE之间的数量关系．



2023年安徽省滁州市定远县郭集学校中考数学一模试卷
参考答案与试题解析
一、选择题（本大题共10小题，共40分。在每小题列出的选项中，选出符合题目的一项）
1． 解：∵﹣|2022|＝﹣2022，﹣2022的相反数是2022，
∴﹣|2022|的相反数是2022，
故选：B．
2． 解：由题意知，原几何体的左视图为一个矩形，矩形的内部有一条横向的虚线．
故选：D．
3． 解：153亿＝15300000000＝1.53×1010．
故选：C．
4． 解：A、2a2•3b3＝6a2b3，故选项错误；
B、（﹣2a）2＝4a2，故选项错误；
C、（a5）2＝a10，故选项错误；
D、，故D正确．
故选：D．
5． 解：设E心里想的数是x，
则G心里想的数应该是10﹣x，
于是F心里想的数是16﹣x，
依题意有：10﹣x+16﹣x＝2×2，
解得x＝11．
故选：D．
6． 解：设城中有x户人家，
依题意得：x+x＝100，
解得：x＝75，
∴城中有75户人家．
故选：B．
7． 解：∵k2≥0，
∴k2+3＞0．
∴反比例函数（k为常数）的函数图象在第一、第三象限；在第一象限内，y随着x的增大而减小；在第三象限内，y随着x的增大而减小．
∵x1＜0＜x2＜x3，
∴y1＜0，y2＞y3＞0，即y1＜y3＜y2．
故选：C．
8． 解：延长BN交AC于D，
在△ANB和△AND中，
，
∴△ANB≌△AND，
∴AD＝AB＝8，BN＝ND，
∵M是△ABC的边BC的中点，
∴DC＝2MN＝6，
∴AC＝AD+CD＝14，
故选：B．

9． 解：∵A（﹣6，10），B（﹣6，0），C（4，0），
∴AB⊥x轴，AB＝10，BC＝10，
∴AC＝10，
∵将△ABC绕点B顺时针旋转一定角度后使A落在y轴上，
∴BA′＝AB＝10，BC′＝BC＝10，A′C′＝AC＝10，
在Rt△OBA′中，OA′＝＝8，
∴A′（0，8），
设C′（a，b），
∴BC′2＝（a+6）2+b2＝100①，A′C′2＝a2+（b﹣8）2＝200②，
①﹣②得b＝③，
把③代入①整理得a2+12a﹣28＝0，
解得a1＝﹣14（舍去），a2＝2，
当a＝2时，b＝﹣6，
∴C′（2，﹣6），
把C′（2，﹣6）代入y＝，
得k＝2×（﹣6）＝﹣12，
∴y＝﹣．
故选：D．
10． 解：当y＝0时，有x2﹣4x+3＝0，
解得：x1＝1，x2＝3，
∴AB＝2．
∵S阴影＝AC•AB＝6，
∴AC＝3，
∴平移后新抛物线的解析式为y＝x2﹣4x+3+3＝x2﹣4x+6．
故选：C．
二、填空题（本大题共4小题，共20分）
11． 解：根据比例中项的概念结合比例的基本性质，得：比例中项的平方等于两条线段的乘积．
所以c2＝4×1，
解得：c＝±2（线段是正数，负值舍去）．
则c＝2cm．
故答案为：2．
12． 解：∵△ABC为正三角形，
∴∠A＝∠B＝60o，
∵∠CPD＝60°，
∴∠BCP+∠BPC＝120°，∠APD+∠BPC＝120°，
∴∠BCP＝∠APD，
∴△BCP∽△APD，
∴BC：AP＝BP：AD，
设等边△ABC的边长为a，
∴BC＝AB＝a，BP＝AB﹣AP＝a﹣x，
∴a：x＝（a﹣x）：y，
∴y＝，
∴y关于x的函数解析式为：y＝﹣x2+x，
∵抛物线的对称轴为：x＝2，
解得：a＝4，
∴等边△ABC的边长为4，
∴y关于x的函数解析式为：y＝﹣x2+x，
把x＝2代入得：y＝1，
∴顶点坐标为（2，1）．
故答案为：（2，1）．
13． 解：∵CF⊥AE，
∴∠AFC＝90°，
∴点F在以AC为直径的圆上运动，
以AC为直径画半圆AC，连接OA，

当点E与B重合时，此时点F与G重合，
当点E与D重合时，此时点F与A重合，
∴点E从点B出发顺时针运动到点D时，点F所经过的路径长为的长，
∵点G为OD的中点，
∴OG＝OD＝OA＝2，
∵OG⊥AB，
∴∠AOG＝60°，AG＝2，
∵OA＝OC，
∴∠ACG＝30°，
∴AC＝2AG＝4，
∴所在圆的半径为2，圆心角为60°，
∴的长为，
故答案为：．
14． 解：∵二次函数对称轴在y轴右侧，与y轴交在正半轴，
∴ab＜0，c＞0，abc＜0．
∴故①不正确；
∵二次函数y＝ax2+bx+c（a≠0）图象的对称轴为直线x＝1，
∴顶点坐标为（1，a+b+c），且开口向下，二次函数的最大值为a+b+c，
故②正确；
∵抛物线过B（﹣1，0），
∴x＝﹣1时，y＝0，即a﹣b+c＝0，
故③不正确；
∵抛物线与x轴有两个交点，
∴b2﹣4ac＞0，
故④不正确；
∵对称轴为直线x＝1，B（﹣1，0），
∴A（3，0），
由图象可知，﹣1＜x＜3时，y＞0，
故⑤正确；
∵x＝﹣＝1，即b＝﹣2a，
而x＝﹣1时，y＝0，即a﹣b+c＝0，
∴a+2a+c＝0，
∴c+3a＝0．
故⑥正确．
故答案为：②⑤⑥．
三、解答题（本大题共9小题，共90分。解答应写出文字说明，证明过程或演算步骤）
15． 解：原式＝÷
＝÷
＝•
＝，
当x＝tan60°﹣tan45°＝﹣1时，
原式＝＝＝．
16． 解：（1）如图，△A1B1C1为所作；

（2）将△ABC先向右平移6个单位，再向下平移2个单位得到△A1B1C1；
故答案为：6；再向下平移2个单位；
（3）如图，△A2B2C2为所作；△A2B2C2与△ABC关于点（﹣3，1）中心对称．
故答案为：（﹣3，1）．
17． 解：（1）①在Rt△ABC中，由勾股定理可得，
∴Rt△ABC斜边AC上的高为；
②当t＝3时，则AP＝6cm，BQ＝4t＝12cm，
∵AB＝16cm，
∴BP＝AB﹣AP＝16﹣6＝10（cm），
在Rt△BPQ中，由勾股定理可得，
即PQ的长为，
故答案为：①9.6cm；②；
（2）由题意可知AP＝2tcm，BQ＝4tcm，
∵AB＝16cm，
∴BP＝AB﹣AP＝16﹣2t（cm），
当△BPQ为等腰三角形时，则有BP＝BQ，即16﹣2t＝4t，
解得，
∴出发秒后△BPQ能形成等腰三角形；
（3）在△ABC中，AC＝20cm，
当点Q在AC上时，AQ＝BC+AC﹣4t＝32﹣4t（cm），CQ＝4t﹣12（cm），
∵△BCQ为等腰三角形，
∴有BQ＝BC、CQ＝BC和CQ＝BQ三种情况，
①当BQ＝BC＝12时，如图，过B作BE⊥AC于E，

则，
由（1）知BE＝9.6cm，
在Rt△BCE中，由勾股定理可得BC2＝BE2+CE2，
即122＝9.62+（2t﹣6）2，
解得t＝6.6或t＝﹣0.6＜0（舍去）；
②当CQ＝BC＝12时，则4t﹣12＝12，解得t＝6；
③当CQ＝BQ时，则∠C＝∠QBC，
∴∠C+∠A＝∠CBQ+∠QBA，
∴∠A＝∠QBA，
∴QB＝QA，
∴，即4t﹣12＝10，解得t＝5.5；
综上可知当运动时间为6.6秒或6秒或5.5秒时，△BCQ为等腰三角形．
18． 解：∵∠BDE＝30°，∠BCE＝60°，
∴∠CBD＝60°﹣∠BDE＝30°＝∠BDE，
∴BC＝CD＝10米，
在Rt△BCE中，sin∠BCD＝，
即BE＝BC•sin60°＝10×＝5米，
AB＝BE+AE＝（5+1）米．
答：旗杆AB的高度是（5+1）米．
19． 解：（1）参加这次调查的学生总人数为6÷15%＝40（人），
故答案为：40；
（2）扇形统计图中，B部分扇形所对应的圆心角是360°×＝108°，
C部分人数为40﹣（6+12+4）＝18（人），
∴C部分扇形所对应的圆心角为360°×＝162°，
故答案为：108°，162°；
（3）补全条形统计图如下：

（4）画树状图为：

共有12种等可能的结果，其中恰好选中1名男生和1名女生的结果为8种，
∴所抽取的2名学生恰好是1名男生和1名女生的概率为＝．
20． 解：（1）∵点A（0，3），点B（4，0），
∴AO＝3，BO＝4．
在Rt△ABO中，由勾股定理得AB＝＝5，
∵四边形ABCD为菱形，
∴AD＝BC＝AB＝5，
∴OC＝5﹣4＝1，
∴点C的坐标为（﹣1，0），点D的坐标为（﹣5，3）．
∴对于直线y1＝mx+n，有，
解得，
∴y＝﹣x﹣
∵双曲线y2＝（x＜0）交于点D，
∴k＝﹣5×3＝﹣15；
（2）由图象可知，当﹣5≤x＜0时，y1≤y2，
所以，当x＜0时，使y1﹣y2≤0的自变量x的取值范围为﹣5≤x＜0，
故答案为﹣5≤x＜0．
21． 证明：（1）∵△ABC是等边三角形，
∴∠BAC＝∠ACB＝∠B＝60°，
∴∠BAD＝∠BAC﹣∠DAE＝60°﹣∠DAE，∠EDC＝∠ACB﹣∠E＝60°﹣∠E，
又∵DA＝DE，
∴∠DAE＝∠E，
∴∠BAD＝∠EDC．
（2）∵点M是点E关于直线BC的对称点，
∴DM＝DE，∠EDC＝∠MDC，
∵DA＝DE，
∴DM＝DA，由（1）可得，∠BAD＝∠EDC，
∴∠MDC＝∠BAD，
∵在△ABD中，∠BAD+∠ADB＝180°﹣∠B＝180°﹣60°＝120°，
∴∠MDC+∠ADB＝120°，
∴∠ADM＝180°﹣（∠MDC+∠ADB）＝60°，
∴△ADM是等边三角形，
∴DM＝AM．
22． 解：（1）设每顶头盔应降价x元，则每顶头盔的销售利润为（68﹣x﹣40）元，平均每周的销售量为（100+20x）顶，
依题意得：（68﹣x﹣40）（100+20x）＝4000，
整理得：x2﹣23x+60＝0，
解得：x1＝3，x2＝20，
∵68﹣x≤58，
∴x≥10，
∴x＝20．
答：每顶头盔应降价20元；
（2）设每周扣除捐赠后可获得利润为w元，每顶头盔售价为a元，
依题意得：w＝[100+20（68﹣a）]（a﹣40﹣m）＝﹣20a2+（20m+2260）a﹣1460（40+m）．
∵抛物线的对称轴为a＝，开口向下，当a≤58时，利润仍随售价的增大而增大，
∴≥58，
解得：m≥3，
又∵1≤m≤5，且m为整数，
∴m＝3或m＝4或m＝5．
23． （1）解：结论：AB＝BC．
理由：如图1中，连接OB．

在Rt△OBC和Rt△OBA中，
，
∴Rt△OBC≌Rt△OBA（HL），
∴AB＝BC．
故答案为：AB＝BC；

（2）证明：延长BA到T，使得AT＝CD．
在△OCD和△OAT中，
，
∴△OCD≌△OAT（SAS），
∴CD＝AT，∠COD＝∠AOT，OD＝OT，
∴∠AOC＝∠DOT，
∵∠AOC＝120°，∠DOE＝60°
∴∠DOE＝∠AOC＝∠DOT，
∴∠DOE＝∠EOT，
在△OED和△EOT中，
，
∴△OED≌△OET（SAS），
∴DE＝ET＝AE+AT＝AE+CD．

（3）解：结论：DE＝AE＝CD．

理由：在AE上截取AT，使得AT＝CD．
在△OCD和△OAT中，
，
∴△OCD≌△OAT（SAS），
∴CD＝AT，∠COD＝∠AOT，OD＝OT，
∴∠AOC＝∠DOT，
∵∠AOC＝120°，∠DOE＝60°
∴∠DOE＝∠AOC＝∠DOT，
∴∠DOE＝∠EOT，
在△OED和△EOT中，
，
∴△OED≌△OET（SAS），
∴DE＝ET＝AE﹣AT＝AE﹣CD．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/3/4 22:19:20；用户：王梓锋；邮箱：18813974184；学号：46897787