山东省枣庄市市中区2022-2023学年七年级上学期期末数学试题（含详细答案）

山东省枣庄市市中区2022-2023学年七年级上学期期末数学试题

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．－的相反数是（    ）

A．－ B． C． D．－

2．如图是正方体的一种展开图，表面上的语句为北京2022年冬奥会和冬残奥会的主题口号“一起向未来！”，那么在正方体的表面与“！”相对的汉字是（　　）

A．一 B．起 C．向 D．来

3．习近平总书记提出了未来五年“精准扶贫”的战略构想，意味着每年要减贫约11700000人，将数据11700000用科学记数法表示为（　　）

A．1.17×107 B．11.7×106 C．0.117×107 D．1.17×108

4．若单项式am﹣1b2与的和仍是单项式，则nm的值是（　　）

A．3 B．6 C．8 D．9

5．用一个平面去截一个正方体，截面不可能是（       ）

A．梯形 B．五边形 C．六边形 D．七边形

6．有理数a，b在数轴上的位置如图所示，则下列各式正确的是（    ）

A． B． C． D．

7．将一副直角三角尺如图放置，若∠AOD=20°，则∠BOC的大小为（ ）

A．140° B．160° C．170° D．150°

8．小明投掷一枚硬币100次，出现“正面朝上”51次，则“正面朝上”的频率为（　　）

A．49 B．51 C．0.49 D．0.51

9．《孙子算经》中有一道题，原文是：今有三人共车，二车空：二人共车，九人步，问人与车各几何？译文为：今有若干人乘车，每3人共乘一车，最终剩余2辆车：若每2人共乘一车，最终剩余9个人无车可乘，问共有多少人，多少辆车？设共有x人，可列方程（    ）

A． B． C． D．

10．如图所示，在这个数据运算程序中，若开始输入的的值为5，第1次运算结果输出的是8，返回进行第二次运算输出的是4，…，则第次输出的结果是（    ）

A．1 B．2 C．4 D．8

二、填空题

11．已知、互为相反数，则______．

12．数轴上点A表示的数是﹣5，将点A在数轴上平移8个单位长度得到点B，则点B表示的数是___________．

13．是关于的方程的解，则的值是__________．

14．对于有理数、，定义一种新运算，规定☆，则3☆__．

15．上午8点30分，钟面上时针与分针的夹角是______．

16．观察下列单项式：，，，，，…按此规律，可以得到第2023个单项式是_________．

三、解答题

17．（1）计算：；

（2）解方程：．

18．先化简，再求值：，其中，．

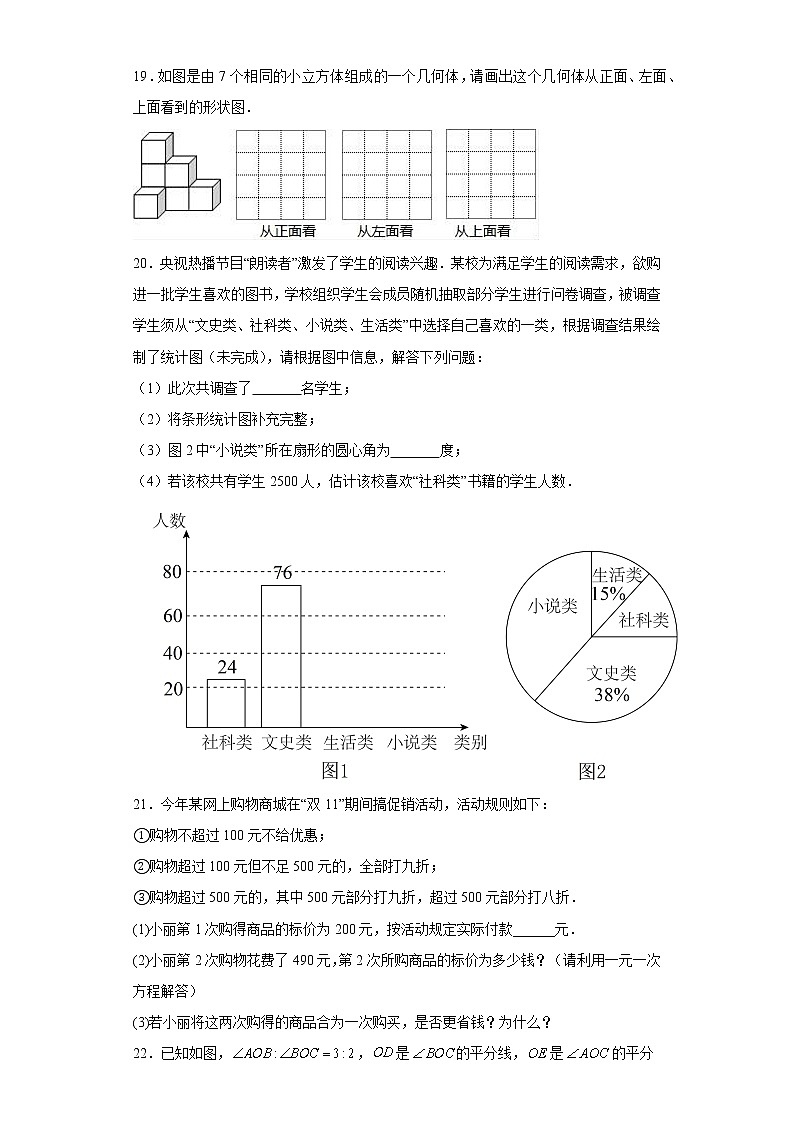
19．如图是由7个相同的小立方体组成的一个几何体，请画出这个几何体从正面、左面、上面看到的形状图．

20．央视热播节目“朗读者”激发了学生的阅读兴趣．某校为满足学生的阅读需求，欲购进一批学生喜欢的图书，学校组织学生会成员随机抽取部分学生进行问卷调查，被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类，根据调查结果绘制了统计图（未完成），请根据图中信息，解答下列问题：

（1）此次共调查了　   　名学生；

（2）将条形统计图补充完整；

（3）图2中“小说类”所在扇形的圆心角为　   　度；

（4）若该校共有学生2500人，估计该校喜欢“社科类”书籍的学生人数．

21．今年某网上购物商城在“双11”期间搞促销活动，活动规则如下：

①购物不超过100元不给优惠；

②购物超过100元但不足500元的，全部打九折；

③购物超过500元的，其中500元部分打九折，超过500元部分打八折．

(1)小丽第1次购得商品的标价为200元，按活动规定实际付款______元．

(2)小丽第2次购物花费了490元，第2次所购商品的标价为多少钱？（请利用一元一次方程解答）

(3)若小丽将这两次购得的商品合为一次购买，是否更省钱？为什么？

22．已知如图，，是的平分线，是的平分线，且，求的度数．

23．如图，已知点C在线段上，M是的中点，点N在线段上，且．

(1)若，求线段的长；

(2)若，则________（直接写出结果）；

(3)若已点知C在线段的延长线上，M是的中点，点N在线段上，，求的长．

24．用火柴棒按图中所示的方法搭图形．

(1)搭第①个图形用______根火柴棒，搭第②图形用______根火柴棒，搭第③个图形用______根火柴棒；

(2)搭第个图形需要多少根火柴棒？

(3)小明发现：按照这种方式搭图形会产生若干个正方形，若使用167根火柴搭图形，图中会产生多少个正方形？

参考答案：

1．B

【分析】只有符号不同的两个数叫做互为相反数，0的相反数是0．根据相反数的定义即可得出答案．

【详解】解：﹣的相反数是，

故选：B．

【点睛】本题考查了相反数，掌握只有符号不同的两个数互为相反数是解题的关键．

2．A

【分析】由平面图形的折叠及立体图形的表面展开图的特点解题．

【详解】解：对于正方体的平面展开图中相对的面一定相隔一个小正方形，由图形可知，与“!”字相对的字是“一”．

故选：A．

【点睛】本题考查生活中的立体图形与平面图形，注意正方体的空间图形，从相对面入手，分析及解答问题．

3．A

【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于等于10时，n是正数；当原数的绝对值小于1时，n是负数．

【详解】11700000=1.17×107．

故选A．

【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

4．C

【分析】首先可判断单项式am-1b2与a2bn是同类项，再由同类项的定义可得m、n的值，代入求解即可．

【详解】解：∵单项式am-1b2与a2bn的和仍是单项式，

∴单项式am-1b2与a2bn是同类项，

∴m-1=2，n=2，

∴m=3，n=2，

∴nm=8．

故选C．

【点睛】本题考查了合并同类项的知识，解答本题的关键是掌握同类项中的两个相同．

5．D

【分析】正方体总共六个面，截面最多为六边形．

【详解】用一个平面去截一个正方体，截面可能是三角形，四边形，五边形，六边形，不可能为七边形，故选D．

【点睛】正方体是六面体，截面最多为六边形．

6．C

【分析】先由数轴上a，b的位置判断出a，b的符号及绝对值的大小，再由各选项进行逐一判断即可．

【详解】解：从数轴可知，，

∴，，，

∴只有选项C符合题意，选项A、B、D都不符合题意，

故选：C．

【点睛】本题考查了数轴上的点表示数，绝对值的意义，有理数的加减以及除法运算，熟知数轴上点所代表的数值的大小关系是解题关键．

7．B

【详解】解：根据∠AOD=20°可得：∠AOC=70°，根据题意可得：∠BOC=∠AOB+∠AOC=90°+70°=160°.

故选B．

8．D

【分析】根据频率=“正面朝上的频数”÷投掷硬币的总数，即可解答．

【详解】解：∵小明投掷一枚硬币100次，出现“正面朝上”51次，

∴“正面朝上”的频率为：，

故选：D．

【点睛】本题考查了频率的定义，熟知定义是解题的关键．

9．B

【分析】设有x人，根据车的辆数不变，即可得出关于x的一元一次方程，此题得解．

【详解】解：设有x人，根据车的辆数不变列出等量关系，

每3人共乘一车，最终剩余2辆车，则车辆数为：，

每2人共乘一车，最终剩余9个人无车可乘，则车辆数为：，

∴列出方程为：．

故选：B．

【点睛】本题考查了由实际问题抽象出一元一次方程，找准等量关系，正确列出一元一次方程是解题的关键．

10．A

【分析】把 代入程序中计算，依此类推得到循环规律，即可得出第 次输出的结果．

【详解】解：把代入得： ，

把 代入得： ，

把 代入得： ，

把 代入得： ，

把 代入得： ，

把 代入得： ，

…，

∴从第2次开始，输出结果以4，2，1这三个数不断循环出现，

∵ ，

∴第次输出的结果是1．

故选：A．

【点睛】本题考查了数字的变化规律，有理数的混合运算，按照程序框图依次运算得出循环规律是解题的关键．

11．

【分析】由、互为相反数，可得，，再整体代入进行计算即可．

【详解】解：∵、互为相反数，

∴，，

∴；

故答案为：．

【点睛】本题考查的是相反数的含义，有理数的除法法则的应用，求解代数式的值，理解相反数的含义是解本题的关键．

12．-13或3##3或-13

【分析】点A在数轴上平移8个单位长度，可以是向左或向右，即向右平移8个单位，即增加8，向左平移就减少8．

【详解】解：如果A向右平移得到，点B表示的数是：，如果A向左平移得到，点B表示的数是：，

故点B表示的数是3或−13．

故答案为：3或−13．

【点睛】此题主要考查了数轴，掌握数轴上的点平移法则是解题关键．数轴上点的平移：向左平移，表示的数减少，向右平移，表示的数增大．

13．-2.

【分析】将x=1代入方程即可解出a.

【详解】将x=1代入方程得:2+a=0,解得a=-2.

故答案为:-2.

【点睛】本题考查解方程,关键在于掌握解方程的步骤.

14．7．

【分析】根据新定义把新运算转化为常规运算进行解答便可．

【详解】解：3☆（﹣2）

＝32﹣|﹣2|

＝9﹣2

＝7，

故答案为：7．

【点睛】本题主要考查了有理数的混合运算，读懂新定义运算是解题的关键．

15．##度

【分析】根据分针每分钟转，时针每分钟转，结合钟面被分成12大格，每大格可计算出30分钟时针与分针所转的角度，所以此时钟面上时针与分针夹角的度数．

【详解】解：30分钟，钟面上时针从8开始转的度数为，

所以此时钟面上时针与分针夹角的度数．

故答案为：．

【点睛】本题考查了钟面角：掌握“钟面被分成12大格，每大格；分针每分钟转，时针每分钟转”是解本题的关键．

16．

【分析】根据题目中的单项式可以发现数字因数和字母的指数的变化特点，即可写出第n个单项式，从而可以写出第2023个单项式．

【详解】解：∵一列单项式：，…，

∴第n个单项式为：，

当时，这个单项式是，

故答案为：．

【点睛】本题考查数字的变化类，解答本题的关键是明确题意，发现数字因数和字母的指数的变化特点，写出相应的单项式．

17．（1）4；（2）

【分析】（1）先计算乘方，再计算乘除，最后算加减即可；

（2）先去分母，再去括号，移项，合并同类项，最后把未知数的系数化“1”即可．

【详解】解：（1）原式；

（2），

去分母得：

去括号得：

整理得：

解得：．

【点睛】本题考查的是含乘方的有理数的混合运算，一元一次方程的解法，掌握“含乘方的有理数的混合运算的运算顺序与解一元一次方程的步骤”是解本题的关键．

18．，-8．

【分析】先去括号，再合并同类项，最后把a、b的值代入化简后的式子计算即可．

【详解】解：

，

把，代入得：

原式=2×（-1）×22=-8．

【点睛】本题考查了整式的化简求值，掌握去括号、合并同类项法则是正确计算的关键．

19．见解析

【分析】根据三视图的定义结合图形画图即可．

【详解】如图所示，

【点睛】本题考查作图-三视图．在画图时一定要将物体的边缘、棱、顶点都体现出来，看得见的轮廓线都画成实线，看不见的画成虚线，不能漏掉．本题画几何体的三视图时应注意小正方形的数目及位置．

20．（1）200；（2）补图见解析；（3）126；（4）300人

【分析】（1）由76÷38%，可得总人数；

（2）结合扇形图，分别求出人数，再画图；

（3）先算社科类百分比，再求小说百分比，再求对应圆心角；

（4）用社科类百分比×2500可得．

【详解】解：（1）此次共调查的人数人；

（2）生活类的人数人，

小说类的人数为人，

补全图形，如下图：

（3）由样本数据可知喜欢“社科类”书籍的学生人数占了总人数的12%，

故答案为：126

（4）由样本数据可知喜欢“社科类”书籍的学生人数占了总人数的12%，

∴该校共有学生2500人，估计该校喜欢“社科类”书籍的学生人数：

2500×12%=300人．

故：该校喜欢“社科类”书籍的学生人数约为300人.

【点睛】本题考查了扇形统计图，条形统计图，用样本估计总体，解题关键是从统计图获取信息．

21．(1)180

(2)550

(3)合为一次购买更省钱

【分析】（1）由购物超过100元但不足500元的，全部打九折；再列式计算即可；

（2）先判断第2次所购商品的标价超过500元，再设第2次所购商品的标价为元．结合题可得：，再解方程即可；

（3）先计算分开购买的付费，合起来购买的付费，再比较即可．

【详解】（1）解：由购物超过100元但不足500元的，全部打九折；可得：

（2）∵，而，

∴第2次所购商品的标价超过500元，

设第2次所购商品的标价为元．

由题可得：，解得；

答：第2次所购商品的标价为550元．

（3），

，

又，，

合为一次购买更省钱．

【点睛】本题考查的是有理数的乘法运算的实际应用，一元一次方程的应用，理解题意，列出正确的运算式与方程是解本题的关键．

22．36°

【详解】试题分析：首先设∠AOB=3x，∠BOC=2x，再根据角平分线性质可得∠AOE═∠AOC＝x，再根据角的和差关系可得∠BOE=∠AOB-∠AOE=3x−x＝x，进而得到x＝12°，再解方程即可得到x=24°，进而得到答案．

试题解析：设，．

则，

∵是的平分线，

∴，

∴，

∵，

∴，

解得，，

∵是的平分线，

∴，

∴，

，

．

23．(1)11

(2)

(3)

【分析】（1）根据M是的中点，可知根据，可知，根据即可求解；

（2）根据（1）的方法求解即可；

（3）根据题意画出图形，根据即可求解

【详解】（1）解： M是的中点，，

，

，

；

（2）解： M是的中点，，

，

，

；

（3）如图，

M是的中点，，

，

，

.

【点睛】本题考查了线段和差的计算，线段中点的性质，等分点的计算，数形结合是解题的关键．

24．(1)7，12，17

(2)搭第个图形需要根火柴棒

(3)98个

【分析】（1）结合图形可直接作答；

（2）根据（1）中的规律求得第n个图形所需火柴棒的根数；

（3）先根据（2）中式子列出一元一次方程，求得167根火柴搭图形，为第多少个，然后方法同（1）数出正方形的个数，进而发现规律即可求解．

【详解】（1）第①个图形为根，

第②个为根，

第③个为根，

故答案为：7，12，17；

（2）由（1）可得第④个为，

……，

第个为，

即：搭第个图形需要根火柴棒；

（3），解得．

第①个图形中有2个正方形：，

第②个图形中有5个正方形：，

第③个图形中有2个正方形，，

……，

第个为个正方形，

若使用167根火柴搭图形，图中会产生98个正方形．

【点睛】本题考查了图形类规律题，找到规律是解题的关键．