陕西省汉中市南郑区2022-2023学年九年级上学期期末数学试题（含详细答案）

这是一份陕西省汉中市南郑区2022-2023学年九年级上学期期末数学试题（含详细答案），共18页。试卷主要包含了单选题，解答题等内容，欢迎下载使用。
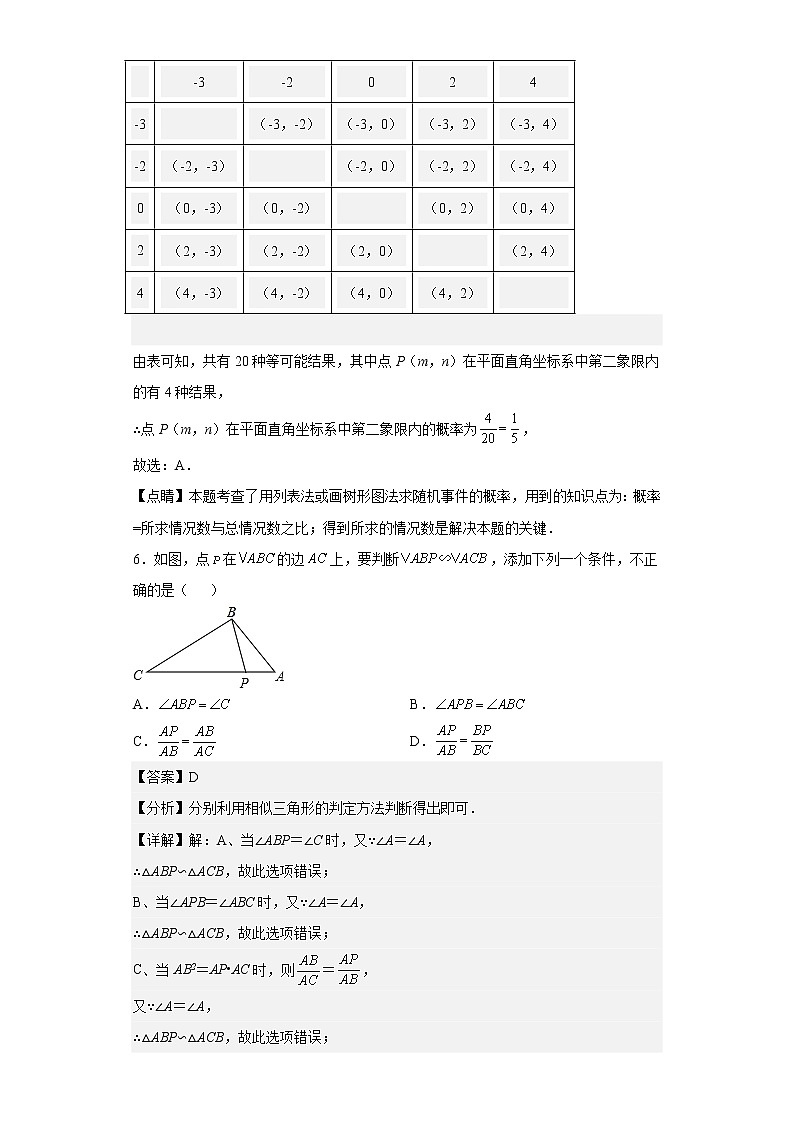
陕西省汉中市南郑区2022-2023学年九年级上学期期末数学试题学校:___________姓名：___________班级：___________考号：___________ 一、单选题1．若，则的值为（    ）A． B． C． D．【答案】A【分析】根据比例性质，设，再代入计算即可．【详解】解：∵，∴设，∴，故选：A．【点睛】本题考查了比例的性质，利用比的意义得出是解题关键．2．计算的值为（    ）A． B．1 C． D．2【答案】C【分析】根据特殊角三角函数值的混合计算法则求解即可．【详解】解：，故选C．【点睛】本题主要考查了特殊角三角函数值的混合计算，熟知相关特殊角的三角函数值是解题的关键．3．反比例函数的图象经过点（1，-2），则k的值为（    ）A． B． C．2 D．【答案】D【分析】根据给定点的坐标利用反比例函数图象上点的坐标特征，即可求出k值，此题得解．【详解】解：∵反比例函数的图象经过点（1，-2），∴k=1×（-2），∴k=-2．故选：D．【点睛】本题考查了反比例函数图象上点的坐标特征，利用反比例函数图象上点的坐标特征找出关于k的一元一次方程是解题的关键．4．下列各种现象属于中心投影的是（    ）A．晚上人走在路灯下的影子 B．中午用来乘凉的树影C．上午人走在路上的影子 D．阳光下旗杆的影子【答案】A【分析】根据中心投影的性质，找到光源是灯光即可得．【详解】解：A、晚上人走在路灯下的影子，光源是灯光，是中心投影，则此项符合题意；B、中午用来乘凉的树影，光源是阳光，是平行投影，则此项不符题意；C、上午人走在路上的影子，光源是阳光，是平行投影，则此项不符题意；D、阳光下旗杆的影子，光源是阳光，是平行投影，则此项不符题意；故选：A．【点睛】本题考查了中心投影，解决本题的关键是理解中心投影的形成光源为灯光．5．点P的坐标是(m，n)，从﹣3，﹣2，0，2，4这五个数中任取一个数作为m的值，再从余下的四个数中任取一个数作为n的值，则点P(m，n)在平面直角坐标系中第二象限内的概率是（    ）A． B． C． D．【答案】A【分析】先画树状图展示所有20种等可能的结果数，再根据第二象限点的坐标特征找出点P（m，n）在平面直角坐标系中第二象限内的结果数，然后根据概率公式求解．【详解】解：列表如下： -3-2024-3 （-3，-2）（-3，0）（-3，2）（-3，4）-2（-2，-3） （-2，0）（-2，2）（-2，4）0（0，-3）（0，-2） （0，2）（0，4）2（2，-3）（2，-2）（2，0） （2，4）4（4，-3）（4，-2）（4，0）（4，2）  由表可知，共有20种等可能结果，其中点P（m，n）在平面直角坐标系中第二象限内的有4种结果，∴点P（m，n）在平面直角坐标系中第二象限内的概率为，故选：A．【点睛】本题考查了用列表法或画树形图法求随机事件的概率，用到的知识点为：概率=所求情况数与总情况数之比；得到所求的情况数是解决本题的关键．6．如图，点在的边上，要判断，添加下列一个条件，不正确的是（　 ）A． B．C． D．【答案】D【分析】分别利用相似三角形的判定方法判断得出即可．【详解】解：A、当∠ABP＝∠C时，又∵∠A＝∠A，∴△ABP∽△ACB，故此选项错误；B、当∠APB＝∠ABC时，又∵∠A＝∠A，∴△ABP∽△ACB，故此选项错误；C、当AB2＝AP•AC时，则＝，又∵∠A＝∠A，∴△ABP∽△ACB，故此选项错误；D、当AB•BC＝AC•BP时，则＝，无法得到△ABP∽△ACB，故此选项正确．故选：D．【点睛】本题考查相似三角形的判定，熟知相似三角形的判定定理是解答此题的关键．7．已知菱形的对角线，的长度是方程的两个实数根，则此菱形的面积为（    ）A．18 B．24 C．30 D．36【答案】A【分析】先根据一元二次方程根与系数关系得到，再利用菱形的面积等于对角线长乘积的一半即可得到答案．【详解】解：∵，的长度是方程的两个实数根，∴，∴菱形的面积．故选：A【点睛】此题考查了一元二次方程根与系数关系、菱形的面积等知识，熟练掌握一元二次方程根与系数关系是解题的关键．8．若、、三点都在函数的图象上，则，，的大小关系是（    ）A． B． C． D．【答案】C【分析】根据反比例函数解析式得到反比例函数经过第二、四象限，在每个象限内y随x增大而增大，据此即可得到答案．【详解】解：∵反比例函数解析式为，∴反比例函数经过第二、四象限，在每个象限内y随x增大而增大，∵、、三点都在函数的图象上，，∴，故选C．【点睛】本题主要考查了比较反比例函数函数值的大小，熟知对于反比例函数，当时，反比例函数经过第一、三象限，在每个象限内y随x增大而减小，当时，反比例函数经过第二、四象限，在每个象限内y随x增大而增大是解题的关键．9．若二次函数y=﹣x2+bx+c的图象的最高点是（﹣1，﹣3），则b、c的值分别是（　　）A．b=2，c=4 B．b=﹣2，c=﹣4 C．b=2，c=﹣4 D．b=﹣2，c=4【答案】B【分析】根据二次函数y=﹣x2+bx+c的二次项系数﹣1来确定该函数的图象的开口方向，由二次函数y=﹣x2+bx+c的图象的最高点是（﹣1，﹣3）确定该函数的顶点坐标，然后根据顶点坐标公式解答b、c的值．【详解】∵二次函数y=﹣x2+bx+c的二次项系数﹣1＜0，∴该函数的图象的开口方向向下，∴二次函数y=﹣x2+bx+c的图象的最高点坐标（﹣1，﹣3）就是该函数的顶点坐标，∴﹣1=﹣，即b=﹣2；①﹣3=，即b2+4c﹣12=0；②由①②解得：b=﹣2，c=﹣4．故选B．【点睛】本题考查了二次函数的最值．解答此题时，弄清楚“二次函数y=﹣x2+bx+c的图象的最高点坐标（﹣1，﹣3）就是该函数的顶点坐标”是解题的关键．10．如图，先画一个边长为1的正方形，以其对角线为边画第二个正方形，再以第二个正方形的对角线为边画第三个正方形，，如此反复下去，…，那么第11个正方形的对角线长为（    ）A． B． C． D．【答案】C【分析】第1个正方形的边长是1，对角线长为；第2个正方形的边长为，对角线长为，第3个正方形的边长为2，对角线长为；得出规律，即可得出结果．【详解】解：由题意得，第1个正方形的边长是1，对角线长为；第2个正方形的边长为，对角线长为，第3个正方形的边长为2，对角线长为；∴第n个正方形的对角线长为，∴第11个正方形的对角线长为故选：C．【点睛】本题主要考查了正方形的性质、勾股定理；求出第一个、第二个、第三个正方形的对角线长，得出规律是解决问题的关键． 二、填空题11．三视图都是圆形的几何体是______．【答案】球【分析】根据三视图的定义求解即可．【详解】解：由题意得，球的三视图都是圆，故答案为：球．【点睛】本题主要考查了简单几何体的三视图，熟知三视图的定义是解题的关键．12．“方胜”是中国古代妇女的一种发饰，其图案由两个全等正方形相叠组成，寓意是同心吉祥，如图，将边长为3cm的正方形ABCD沿对角线BD方向平移1cm得到正方形，形成一个“方胜”图案，则点D，之间的距离为______．【答案】##【分析】根据正方形的性质、勾股定理求出BD，根据平移的性质求出，计算即可．【详解】解：根据题意得：，，∠A=90°，∴，∴，即点D，之间的距离为．故答案为：．【点睛】本题考查的是平移的性质、正方形的性质，勾股定理，根据平移的性质求出是解题的关键．13．如图，是由8个大小相同的小正方体堆砌而成的几何体，现从标有①、②、③、④的四个小正方体中随机取走一个，所得新几何体与原几何体主视图相同的概率是______．【答案】##25%##0.25【分析】根据题意得到原几何体的主视图，结合主视图在①、②、③、④选择符合题意的序号，从而得到答案．【详解】原几何体的主视图是：故取走正方体①使所得新几何体与原几何体主视图相同，其概率为，故答案为：．【点睛】本题考查了简单组合体的三视图．视图中每一个闭合的线框都表示物体上的一个平面，而相连的两个闭合线框常不在一个平面上，解题的关键是画出原几何体的主视图．14．若，则由表中的信息可知与之间的函数关系式是_______________．-101  183   【答案】【分析】利用待定系数法即可求二次函数关系式．【详解】解：把，代入得：，解得：，所以抛物线解析式为．故答案为．【点睛】本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．15．如图所示是一块含30°，60°，90°的直角三角板，直角顶点O位于坐标原点，斜边AB垂直于x轴，顶点A在函数的图象上，顶点B在函数的图象上，∠ABO＝30°，则_____．【答案】﹣3【分析】设AC＝a，则OA＝2a，可得OC＝a，根据直角三角形30°角的性质和勾股定理分别计算点A和B的坐标，写出A和B两点的坐标，代入解析式求出和的值，相比即可．【详解】解：如图，Rt△AOB中，∠B＝30°，∠AOB＝90°，∴∠OAB＝60°，∵AB⊥x轴， ∴∠ACO＝90°，∴∠AOC＝30°，设AC＝a，则OA＝2a，∴OC＝a，∴A（a，a），∵顶点A在函数（x＞0）的图象上，∴a×a＝a2，在Rt△BOC中，OB＝2OC＝2a，∴BC＝＝3a，∴B（a，﹣3a），∵顶点B在函数（x＞0）的图象上，∴﹣3a×a＝﹣3，∴＝﹣3，故答案为：﹣3．【点睛】本题考查了反比例函数图象上点的特征、直角三角形30°的性质，熟练掌握直角三角形30°角所对的直角边是斜边的一半，正确写出A、B两点的坐标是关键． 三、解答题16．用适当的方法解方程：(1)(2)【答案】(1)，(2)， 【分析】（1）根据因式分解法解一元二次方程即可求解；（2）根据因式分解法解一元二次方程即可求解．【详解】（1）解： 或∴，．（2）解：或∴，【点睛】本题考查了解一元二次方程，掌握解一元二次方程的方法是解题的关键．17．如图，在△ABC中，点D是AB上一点，且AD＝1，AB＝3，．求证：△ACD∽△ABC．【答案】见解析【分析】首先利用已知得出，进而利用相似三角形的判定方法得出即可．【详解】证明：AD＝1，AB＝3，AC＝，      又 ∽【点睛】此题主要考查了相似三角形的判定，正确把握相似三角形的判定方法是解题关键．18．万科广场已成为人们周末休闲娱乐的重要场所，从一楼到二楼有一自动扶梯（如图1），图2是侧面示意图，已知自动扶梯的坡度（或坡比），米，是二楼楼顶，，点B在上且在自动扶梯顶端C的正上方，若，在自动扶梯底端A处测得B点仰角为40°，求二楼的层高．（精确到0．1米，参考数据：）【答案】米【分析】如图所示，延长交于D，先解求出米，米，再解，求出的长即可得到答案．【详解】解：如图所示，延长交于D，∵，，∴，即，∵自动扶梯的坡度（或坡比），∴，∴，在中，由勾股定理得：，∴，∴米（负值舍去），∴米，在中，，∴米，∴米，∴二楼的层高约为米．【点睛】本题主要考查了解直角三角形的实际应用，勾股定理，正确作出辅助线构造直角三角形是解题的关键．19．实践与操作：如图，在平面直角坐标系中，点A、点B的坐标分别为，．(1)画出绕点顺时针旋转后的；(2)点是的中点，在（1）的条件下，的对应点的坐标为______．(3)以点为位似中心，相似比为，在轴的上方画出放大后的．【答案】(1)见解析(2)(3)见解析 【分析】根据旋转的性质作图即可．由题意得，点是的中点，利用中点坐标公式求解即可．根据位似的性质作图即可．【详解】（1）如图，即为所求．（2）点是的中点，点是的中点，点的坐标为 ,故答案为：．（3）如图，即为所求．【点睛】本题考查了作图——旋转变换、位似变换，熟练掌握旋转和位似的性质是解答本题的关键．20．已知反比例函数上的图象与一次函数的图象交于点和点．(1)求的函数关系式；(2)观察图象，直接写出使得成立的自变量x的取值范围；(3)如果点C与点A关于x轴对称，求的面积．【答案】(1)(2)或(3) 【分析】（1）先把点A坐标代入反比例函数解析式，求出反比例函数解析式，再把点B坐标代入反比例函数解析式求出点B的坐标，然后把A、B坐标代入一次函数解析式中求出一次函数解析式即可；（2）利用图象法求解即可；（3）根据关于x轴对称的点横坐标相同，纵坐标互为相反数求出点C的坐标，进而求出，再根据进行求解即可．【详解】（1）解：把点代入反比例函数中得：，，∴，∴，把代入中得：，∴，∴，把，代入中得：，∴，∴；（2）解：由函数图象可知，当或时，；（3）解：∵点C与点A关于x轴对称，∴点C的坐标为，∴，∴．【点睛】本题主要考查了反比例函数与一次函数综合，坐标与图形变化—轴对称，灵活运用所学知识是解题的关键．21．如图，抛物线与x轴交于A，B两点，它们的对称轴与x轴交于点N，过顶点M作ME⊥y轴于点E，连接BE交MN于点F.已知点A的坐标为（﹣1，0）.（1）求该抛物线的解析式及顶点M的坐标；（2）求△EMF与△BNF的面积之比.【答案】（1），（1，4）；（2）.【分析】（1）直接将（﹣1，0）代入求出即可，再利用配方法求出顶点坐标，（2）利用EM∥BN，则△EMF∽△BNF，进而求出△EMF与△BNE的面积之比．【详解】解：（1）∵点A在抛物线上，∴，解得：c=3，∴抛物线的解析式为.∵，∴抛物线的顶点M（1，4）；（2）∵A（﹣1，0），抛物线的对称轴为直线x=1，∴点B（3，0）.∴EM=1，BN=2.∵EM∥BN，∴△EMF∽△BNF.∴． 22．如图，在中，，D是边的中点，过B作，交的延长线于点E，，，求：(1)线段的长；(2)的值．【答案】(1)(2) 【分析】（1）先解求出，再根据直角三角形斜边上的中线等于斜边的一半即可得到答案；（2）先利用勾股定理求出，再证明，推出，解求出，利用勾股定理求出，则．【详解】（1）解：∵在中，，，，∴，∵D是边的中点，∴；（2）解：在在中，，，，∴，∵D是边的中点，∴，∴，∴∵，∴，∴，∴．【点睛】本题主要考查了解直角三角形，勾股定理，直角三角形斜边上的中线的性质，等腰三角形的性质与判定等等，熟知解直角三角形的方法是解题的关键．23．我国古代数学家赵爽利用影子对物体进行测量的方法，在至今仍有借鉴意义．(1)如图1已知小明的身高是1.6米，他在路灯AB下的影子长为2米，此时小明距路灯灯杆的底部3米，求灯杆AB的高度；(2)如图2现将一高度为2米的木杆CG放在灯杆AB前，测得其影长CH为1米，再将木杆沿着BC方向移动1.8米至DE的位置，此时测得其影长DF为3米，求灯杆AB的高度．【答案】(1)灯杆AB的高度为4米(2)灯杆AB的高度为米 【分析】（1）利用平行线分线段成比例的推论可知，代入求解即可；（2）同（1）可得，，先求出BC，进而求出AB．【详解】（1）解：由题意可知，，，∴，由题意，，∴，即，解得，∴灯杆AB的高度为4米；（2）解：由题意可知，，，，∵中，，∴，即，同理，中，，∴，即，∴解得，∴，∴，∴灯杆AB的高度为米．【点睛】本题考查平行线分线段成比例定理的实际应用，解题的关键是掌握平行线分线段成比例定理的推论：平行于三角形一边，并且和其他两边相交的直线，所截得的三角形的三边与原三角形的三边对应成比例．