高中数学高考19第四章 三角函数、解三角形 4 2 同角三角函数基本关系式及诱导公式

这是一份高中数学高考19第四章 三角函数、解三角形 4 2 同角三角函数基本关系式及诱导公式，共8页。试卷主要包含了同角三角函数的基本关系，诱导公式等内容，欢迎下载使用。
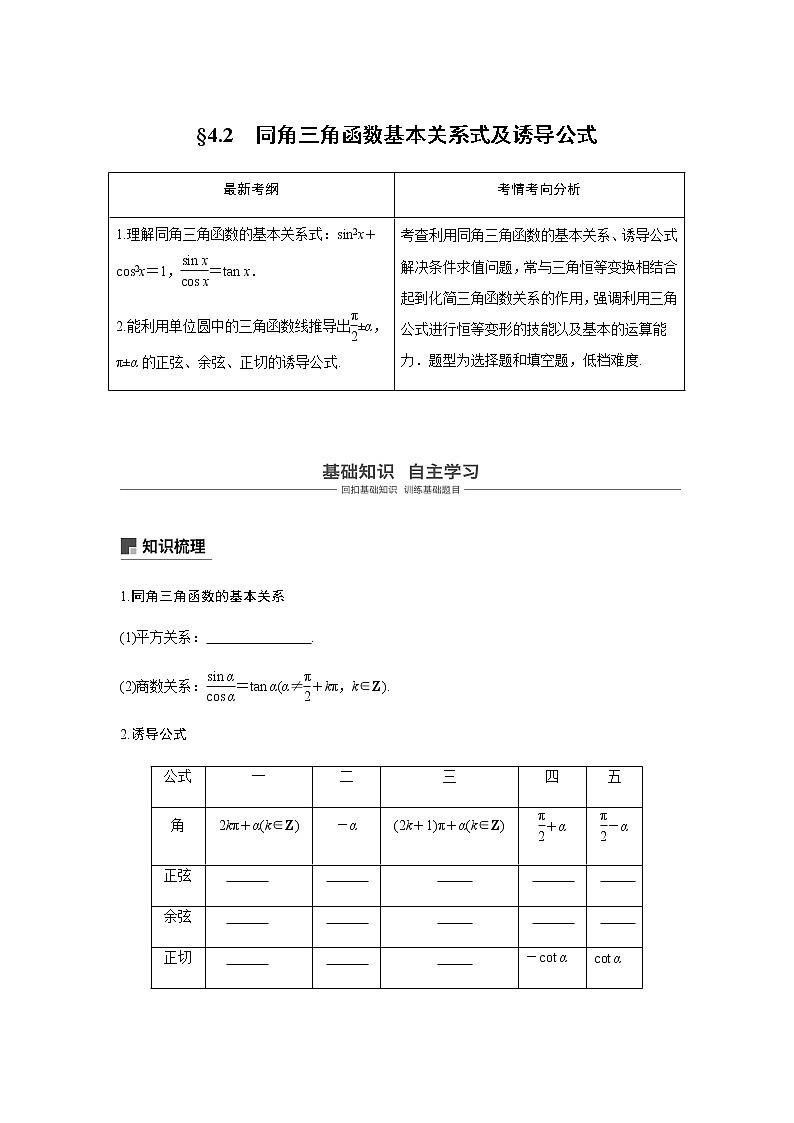
§4.2　同角三角函数基本关系式及诱导公式最新考纲考情考向分析1.理解同角三角函数的基本关系式：sin2x＋cos2x＝1，＝tan x．2.能利用单位圆中的三角函数线推导出±α，π±α的正弦、余弦、正切的诱导公式.考查利用同角三角函数的基本关系、诱导公式解决条件求值问题，常与三角恒等变换相结合起到化简三角函数关系的作用，强调利用三角公式进行恒等变形的技能以及基本的运算能力．题型为选择题和填空题，低档难度. 1.同角三角函数的基本关系(1)平方关系：               .(2)商数关系：＝tan α(α≠＋kπ，k∈Z).2.诱导公式公式一二三四五角2kπ＋α(k∈Z)－α(2k＋1)π＋α(k∈Z)＋α－α正弦                                        余弦                                        正切                           －cot αcot α口诀函数名不变符号看象限函数名改变符号看象限 概念方法微思考1．使用平方关系求三角函数值时，怎样确定三角函数值的符号？提示　根据角所在象限确定三角函数值的符号．2．诱导公式记忆口诀：“奇变偶不变，符号看象限”中的奇、偶是何意义？提示　所有诱导公式均可看作k·±α(k∈Z)和α的三角函数值之间的关系，口诀中的奇、偶指的是此处的k是奇数还是偶数．题组一　思考辨析1．判断下列结论是否正确(请在括号中打“√”或“×”)(1)若α，β为锐角，则sin2α＋cos2β＝1.(　 　)(2)若α∈R，则tan α＝恒成立．(　 　)(3)sin(π＋α)＝－sin α成立的条件是α为锐角．(　 　)(4)若sin(kπ－α)＝(k∈Z)，则sin α＝.(　 　)题组二　教材改编2．若sin α＝，<α<π，则tan α＝        .3．已知tan α＝2，则的值为      ．4．化简·sin(α－π)·cos(2π－α)的结果为        ．题组三　易错自纠5．已知sin αcos α＝，且<α<，则cos α－sin α的值为        ．6．(2018·鄂尔多斯诊断)已知α为锐角，cos＝，则cos(π＋α)＝        .7．已知cos α＝，－<α<0，则的值为        ．题型一　同角三角函数基本关系式的应用1．已知α是第四象限角，sin α＝－，则tan α等于(　　)A．－  B.  C．－  D.2．若tan α＝，则cos2α＋2sin 2α等于(　　)A.  B.  C．1  D.3．若角α的终边落在第三象限，则＋的值为(　　)A．3  B．－3  C．1  D．－14．已知cos x＋sin x＝，x∈(0，π)，则tan x等于(　　)A．－   B．－C．2   D．－2思维升华 (1)利用sin2α＋cos2α＝1可实现正弦、余弦的互化，开方时要根据角α所在象限确定符号；利用＝tan α可以实现角α的弦切互化．(2)应用公式时注意方程思想的应用：对于sin α＋cos α，sin αcos α，sin α－cos α这三个式子，利用(sin α±cos α)2＝1±2sin αcos α，可以知一求二．(3)注意公式逆用及变形应用：1＝sin2α＋cos2α，sin2α＝1－cos2α，cos2α＝1－sin2α.题型二　诱导公式的应用例1 (1)已知A＝＋(k∈Z)，则A的值构成的集合是(　　)A．{1，－1,2，－2}   B．{－1,1}C．{2，－2}   D．{1，－1,0,2，－2}(2)化简：＝        .思维升华 (1)诱导公式的两个应用①求值：负化正，大化小，化到锐角为终了．②化简：统一角，统一名，同角名少为终了．(2)含2π整数倍的诱导公式的应用由终边相同的角的关系可知，在计算含有2π的整数倍的三角函数式中可直接将2π的整数倍去掉后再进行运算．如cos(5π－α)＝cos(π－α)＝－cos α.跟踪训练1 (1)已知角α终边上一点P(－4,3)，则的值为        ．(2)已知f(α)＝(sin α≠0,1＋2sin α≠0)，则f＝        .题型三　同角三角函数基本关系式和诱导公式的综合应用例2 (1)(2018·铁岭模拟)已知cos＝，且－π<α<－，则cos等于(　　)A.   B.C．－   D．－ (2)已知－π<x<0，sin(π＋x)－cos x＝－.①求sin x－cos x的值；  ②求的值．  引申探究本例(2)中若将条件“－π<x<0”改为“0<x<π”，求sin x－cos x的值．  思维升华 (1)利用同角三角函数的基本关系式和诱导公式求值或化简时，关键是寻求条件、结论间的联系，灵活使用公式进行变形．(2)注意角的范围对三角函数符号的影响．跟踪训练2 (1)(2018·营口模拟)已知角θ的终边在第三象限，tan 2θ＝－2，则sin2θ＋sin(3π－θ)cos(2π＋θ)－cos2θ等于(　　)A．－  B.  C．－  D.(2)已知函数f(x)＝asin(πx＋α)＋bcos(πx＋β)，且f(4)＝3，则f(2 019)的值为(　　)A．－1   B．1C．3   D．－31．已知α是第四象限角，tan α＝－，则sin α等于(　　)A.  B．－  C.  D．－2．已知α为锐角，且sin α＝，则cos(π＋α)等于(　　)A．－  B.  C．－  D.3．(2018·包头质检)已知sin(π＋θ)＝－cos(2π－θ)，|θ|<，则θ等于(　　)A．－  B．－  C.  D.4．(2018·盘锦质检)已知α∈，且cos α＝－，则等于(　　)A.  B．－  C.  D．－5．已知tan θ＝2，则的值为(　　)A.  B．1  C．－  D．－16．(2018·营口检测)已知sin＝，α∈，则sin(π＋α)等于(　　)A.  B．－  C.  D．－7．若θ∈，则等于(　　)A．sin θ－cos θ   B．cos θ－sin θC．±(sin θ－cos θ)   D．sin θ＋cos θ8．已知sin x＋cos x＝，x∈(0，π)，则tan x等于(　　)A．－  B.  C.  D．－9．在△ABC中，若tan A＝，则sin A＝        .10．(2018·朝阳检测)sin π·cos π·tan的值是        ．11．已知0<α<，若cos α－sin α＝－，则的值为        ．12．(2018·葫芦岛模拟)已知k∈Z，化简：＝      .13．若sin θ，cos θ是方程4x2＋2mx＋m＝0的两根，则m的值为(　　)A．1＋   B．1－C．1±   D．－1－14．已知α为第二象限角，则cos α＋sin α ＝        .15．已知α，β∈，且sin(π－α)＝cos.cos(－α)＝－cos(π＋β)，求α，β.    16．已知cos＋sin＝1.求cos2＋cos β－1的取值范围．