中考数学二轮复习几何专项复习专题13 几何最值之瓜豆原理知识精讲

几何最值之瓜豆原理知识精讲

初中数学有一类动态问题叫做主从联动，这类问题应该说是非常出题，好多优秀老师都在研究它，原因是它在很多名校模考的时候经常出现，有的老师叫他瓜豆原理，个人理解可能是种瓜得瓜种豆得豆的意思吧，主动点运动的轨迹是什么，则从动点的轨迹就是什么。也有的老师叫他旋转相似，或者手拉手。我感觉这类问题在解答的时候需要有轨迹思想，就是先要明确主动点的轨迹，然后要搞清楚主动点和从动点的关系，进而确定从动点的轨迹来解决问题，但在解答问题时，要符合解不超纲的原则，所以最后解决问题还是用到了旋转相似的知识，也就是动态手拉手模型，下面整理一些题目来集中训练一下这类题目，希望对你能有所帮助.

涉及的知识和方法：

知识：①相似；②三角形的两边之和大于第三边；③点到直线之间的距离垂线段最短；④点到圆上点共线有最值。

方法：第一步：找主动点的轨迹 ；第二步：找从动点与主动点的关系；第三步：找主动点的起点和终点；第四步：通过相似确定从动点的轨迹，第五步：根据轨迹确定点线、点圆最值

在此类题目中，题目或许先描述的是主动点P，但最终问题问的可以是另一点Q(从动点)，根据P、Q之间存在某种联系，从P点出发探讨Q点运动轨迹并求出最值。

一、轨迹之圆篇

例1：如图，P是圆O上一个动点，A为定点，连接AP，Q为AP中点．

考虑：当点P在圆O上运动时，Q点轨迹是？

分析观察动图可知点Q轨迹是个圆，而我们还需确定的是此圆与圆O有什么关系？

考虑到Q点始终为AP中点，连接AO，取AO中点M，则M点即为Q点轨迹圆圆心，半径MQ是OP一半，任意时刻，均有△AMQ∽△AOP，QM:PO=AQ:AP=1:2．

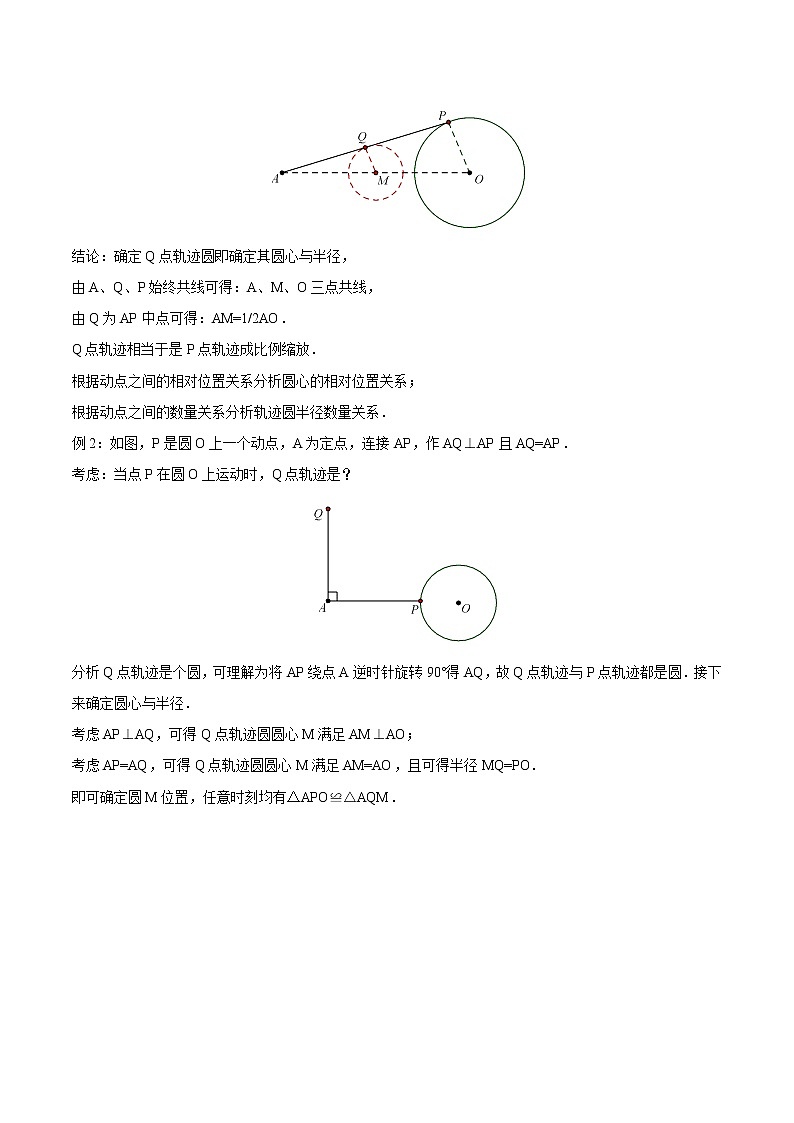
结论：确定Q点轨迹圆即确定其圆心与半径，

由A、Q、P始终共线可得：A、M、O三点共线，

由Q为AP中点可得：AM=1/2AO．

Q点轨迹相当于是P点轨迹成比例缩放．

根据动点之间的相对位置关系分析圆心的相对位置关系；

根据动点之间的数量关系分析轨迹圆半径数量关系．

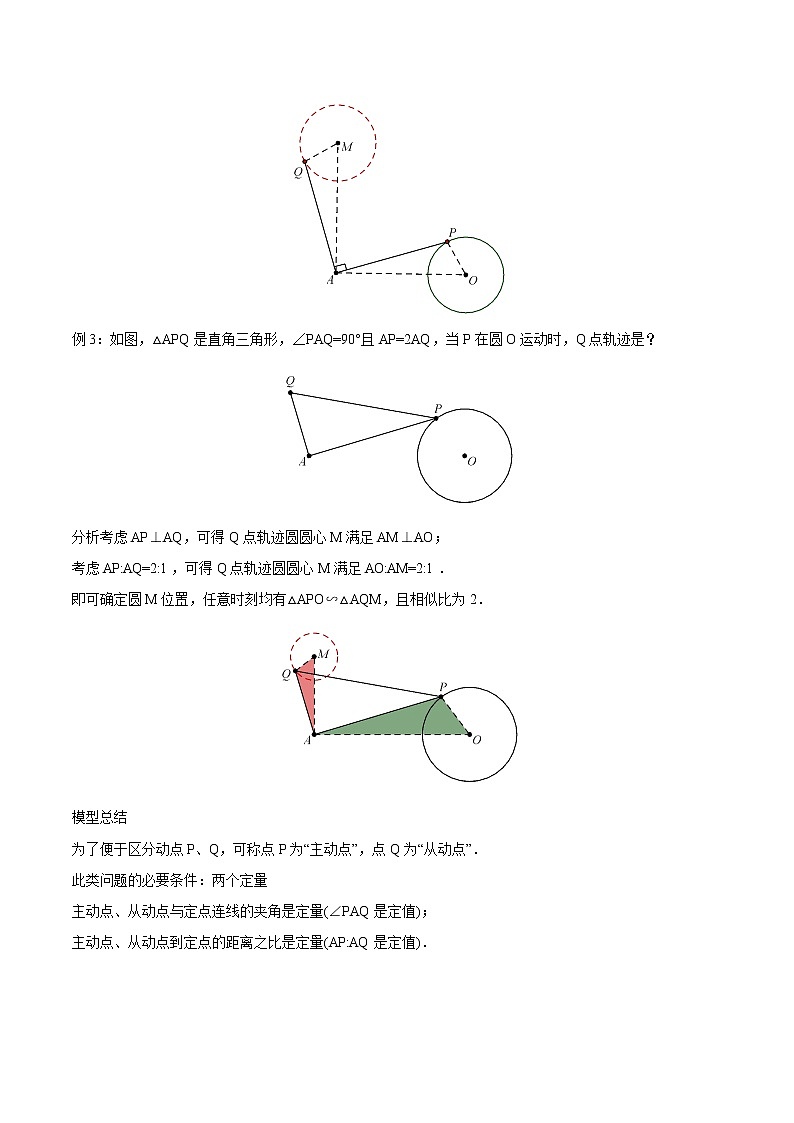
例2：如图，P是圆O上一个动点，A为定点，连接AP，作AQ⊥AP且AQ=AP．

考虑：当点P在圆O上运动时，Q点轨迹是？

分析Q点轨迹是个圆，可理解为将AP绕点A逆时针旋转90°得AQ，故Q点轨迹与P点轨迹都是圆．接下来确定圆心与半径．

考虑AP⊥AQ，可得Q点轨迹圆圆心M满足AM⊥AO；

考虑AP=AQ，可得Q点轨迹圆圆心M满足AM=AO，且可得半径MQ=PO．

即可确定圆M位置，任意时刻均有△APO≌△AQM．

例3：如图，△APQ是直角三角形，∠PAQ=90°且AP=2AQ，当P在圆O运动时，Q点轨迹是？

分析考虑AP⊥AQ，可得Q点轨迹圆圆心M满足AM⊥AO；

考虑AP:AQ=2:1，可得Q点轨迹圆圆心M满足AO:AM=2:1．

即可确定圆M位置，任意时刻均有△APO∽△AQM，且相似比为2．

模型总结

为了便于区分动点P、Q，可称点P为“主动点”，点Q为“从动点”．

此类问题的必要条件：两个定量

主动点、从动点与定点连线的夹角是定量(∠PAQ是定值)；

主动点、从动点到定点的距离之比是定量(AP:AQ是定值)．

结论(1)主、从动点与定点连线的夹角等于两圆心与定点连线的夹角：

∠PAQ=∠OAM；

(2)主、从动点与定点的距离之比等于两圆心到定点的距离之比：

AP:AQ=AO:AM，也等于两圆半径之比．

按以上两点即可确定从动点轨迹圆，Q与P的关系相当于旋转+伸缩．

古人云：种瓜得瓜，种豆得豆．“种”圆得圆，“种”线得线，谓之“瓜豆原理”．

思考1：如图，P是圆O上一个动点，A为定点，连接AP，以AP为一边作等边△APQ．

考虑：当点P在圆O上运动时，Q点轨迹是？

分析Q点满足(1)∠PAQ=60°；(2)AP=AQ，故Q点轨迹是个圆：

考虑∠PAQ=60°，可得Q点轨迹圆圆心M满足∠MAO=60°；

考虑AP=AQ，可得Q点轨迹圆圆心M满足AM=AO，且可得半径MQ=PO．

即可确定圆M位置，任意时刻均有△APO≌△AQM．

小结可以理解AQ由AP旋转得来，故圆M亦由圆O旋转得来，旋转角度与缩放比例均等于AP与AQ的位置和数量关系．

思考2如图，P是圆O上一个动点，A为定点，连接AP，以AP为斜边作等腰直角△APQ．

考虑：当点P在圆O上运动时，如何作出Q点轨迹？

分析Q点满足(1)∠PAQ=45°；(2)AP:AQ=：1，故Q点轨迹是个圆．

连接AO，构造∠OAM=45°且AO:AM=：1．M点即为Q点轨迹圆圆心，此时任意时刻均有△AOP∽△AMQ．即可确定点Q的轨迹圆．

二、轨迹之线段篇

引例：如图，P是直线BC上一动点，连接AP，取AP中点Q，当点P在BC上运动时，Q点轨迹是？

分析当P点轨迹是直线时，Q点轨迹也是一条直线．

可以这样理解：分别过A、Q向BC作垂线，垂足分别为M、N，在运动过程中，因为AP=2AQ，所以QN始终为AM的一半，即Q点到BC的距离是定值，故Q点轨迹是一条直线．

引例如图，△APQ是等腰直角三角形，∠PAQ=90°且AP=AQ，当点P在直线BC上运动时，求Q点轨迹？

分析当AP与AQ夹角固定且AP:AQ为定值的话，P、Q轨迹是同一种图形．

当确定轨迹是线段的时候，可以任取两个时刻的Q点的位置，连线即可，比如Q点的起始位置和终点位置，连接即得Q点轨迹线段．

模型总结

必要条件：

主动点、从动点与定点连线的夹角是定量(∠PAQ是定值)；

主动点、从动点到定点的距离之比是定量(AP:AQ是定值)．

结论：

P、Q两点轨迹所在直线的夹角等于∠PAQ(当∠PAQ≤90°时，∠PAQ等于MN与BC夹角)

P、Q两点轨迹长度之比等于AP:AQ(由△ABC∽△AMN，可得AP:AQ=BC:MN)