6.5 构造常见几何体巧解立体几何小题 讲义-高考数学一轮复习解题技巧方法

这是一份6.5 构造常见几何体巧解立体几何小题 讲义-高考数学一轮复习解题技巧方法，文件包含第六章第5节构造常见几何体巧解立体几何小题-解析版docx、第六章第5节构造常见几何体巧解立体几何小题-原卷版docx等2份试卷配套教学资源，其中试卷共14页， 欢迎下载使用。
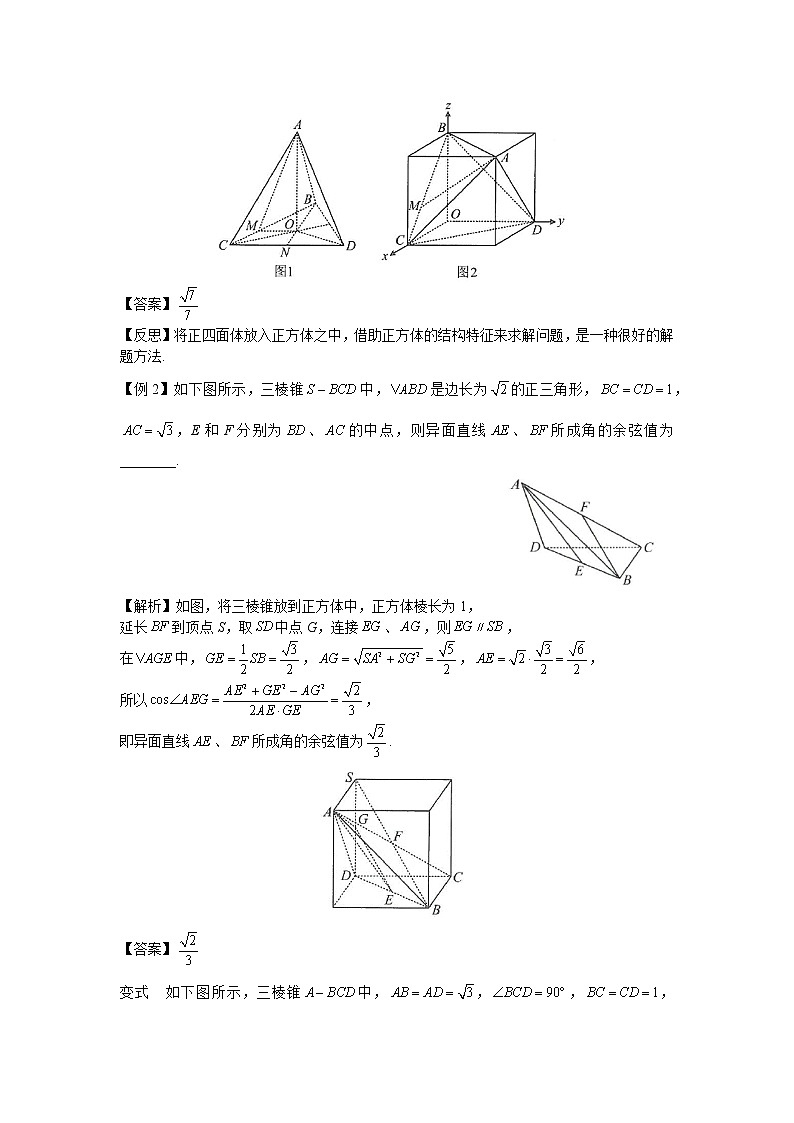
第5节  构造常见几何体巧解立体几何小题（新高考、理科专用）知识与方法若立体几何问题的题干并没有给出图形，而是直接描述一些点、线、面的位置关系，或所给图形的立体感不强，这类题直接想象图形往往难度较大，此时可构造常见的几何体模型（如正方体、长方体等），运用这些几何体较强的立体感来辅助进行空间想象，是较好的处理方法. 典型例题【例1】在正四面体中，M为的中点，则直线与平面所成角的正弦值为________.【解析】如图1，设平面于O，则O是正三角形的中心，不妨设，则，，，所以，故直线与平面所成角的正弦值为解法2：如图2，将正四面体放到正方体中，设正方体棱长为2，则，，所以，易得平面的法向量可取，故从而直线与平面所成角的正弦值为【答案】变式1  在正四面体中，点M在棱上，且，则直线与平面所成角的正弦值为________.【解析】如图1，设N是中点，平面于O，则O是正三角形的中心，，设，易求得，，，，，所以，从而直线与平面所成角的正弦值为.解法2：如图2，将正四面体放到正方体中，设正方体棱长为3，则，，所以，易得平面的法向量可取，故从而直线与平面所成角的正弦值为【答案】变式2  在正四面体中，点M在棱上，且，则异面直线与所成角的余弦值为________.【解析】解法1：如图1，设N是的中点，平面于O，则O是正三角形的中心，显然，所以，设，易求得，，，，所以，故异面直线与所成角的余弦值为.解法2：如图2，将正四面体放入正方体，设正方体棱长为3，则，，，，所以，，故从而异面直线与所成角的余弦值为.【答案】【反思】将正四面体放入正方体之中，借助正方体的结构特征来求解问题，是一种很好的解题方法.【例2】如下图所示，三棱锥中，是边长为的正三角形，，，E和F分别为、的中点，则异面直线、所成角的余弦值为________.【解析】如图，将三棱锥放到正方体中，正方体棱长为1，延长到顶点S，取中点G，连接、，则，在中，，，，所以，即异面直线、所成角的余弦值为.【答案】变式  如下图所示，三棱锥中，，，，，E和F分别为、中点，则异面直线、所成角的余弦值为________.【解析】如图，将三棱锥放入长方体中，其中，，容易验证满足题干条件，取中点G，连接、，易证为平行四边形，故，在中，，，，所以，故异面直线、所成角的余弦值为.【答案】【例3】二面角的大小为45°，，于M，，，，则异面直线与所成角的余弦值为（    ）A. B. C. D.【解析】构造如图所示的正方体，并将底面向右扩展一个正方形，将平移至处，容易看出与成60°角，所以异面直线与所成角的余弦值为.【答案】D变式1  二面角的大小为60°，，于M，，，，则异面直线与所成角的余弦值为（    ）A. B. C. D.【解析】构造如图所示的长方体，其中底面是边长为1的正方形，高为，二面角即为二面角，容易验证满足二面角的大小为60°，将平移至处，在中，易求得，，，所以，故异面直线与所成角的余弦值为.【答案】B变式2  二面角的大小为60°，，于M，，，，则直线与平面所成角的正弦值为（    ）A. B. C. D.【解析】构造如图所示的长方体，长、宽、高分别为1、1、，平面即为，平面即为，二面角即为二面角，容易验证满足二面角的大小为60°，过Q作于T，显然，所以平面，故即为直线与平面所成角，易求得，，所以.【答案】D【反思】二面角模型下的空间计算问题，通过构造长方体，借助长方体较强的立体感来求解问题，是较好的处理方法.强化训练1.（★★★）正四面体中，点M、N都在棱上，，则异面直线与所成角的余弦值为______.【解析】将正四面体放入正方体中，建立如图所示的坐标系，设正方体棱长为3，则，，，，所以，，从而故异面直线与所成角的余弦值为.【答案】2.（★★★）如下图所示，三棱锥中，是等腰直角三角形，，，，则直线与平面所成角的正弦值为（    ）A. B. C. D.【解析】如图，将三棱锥放入正方体中，由正方体的结构特征知平面，设与平面交于点E，则E为的中心，即为直线与平面所成角，易求得，，所以，故，即直线与平面所成角的正弦值为.【答案】A3.（★★★）如下图所示，三棱锥中，，，，，则点C到平面的距离为_______.【解析】如图，将三棱锥放入长方体中，其中，，容易验证满足题干条件，易证平面，过E作于F，则，所以平面，在中，，，所以，，故点E到平面的距离为，因为中点为O，所以点C到平面ABD的距离也为【答案】 4．（★★★）二面角的大小为60°，，，A为垂足，，，且，，，，则______.【解析】如图，将二面角放到长方体中考虑，其中四边形和均为正方形，平面即为，平面即为，显然即为二面角的平面角，所以，由题意，，，，，，，满足题干所有条件，所以.【答案】5.（★★★）如下图所示，在所有棱长均相等的平行六面体中，，则二面角的余弦值为______.【解析】如图，由题意，不难发现整个图形局部的四面体是正四面体，作平面于E，则E在上且为正的中心，取中点F，连接，，则，，所以即为二面角的平面角，设，易求得，，从而，故二面角的余弦值为.【答案】