高中数学高考78第十三章 系列4选讲 13 1 坐标系与参数方程 第1课时 坐标系课件PPT

这是一份高中数学高考78第十三章 系列4选讲 13 1 坐标系与参数方程 第1课时 坐标系课件PPT，共58页。PPT课件主要包含了内容索引，课时作业，基础知识自主学习，题型分类深度剖析等内容，欢迎下载使用。
NEIRONGSUOYIN
基础知识 自主学习
题型分类 深度剖析
设点P(x，y)是平面直角坐标系中的任意一点，在变换φ：________________的作用下，点P(x，y)对应到点P′(x′，y′)，称φ为平面直角坐标系中的坐标伸缩变换，简称伸缩变换.
ZHISHISHULI
2.极坐标系(1)极坐标与极坐标系的概念在平面内取一个定点O，自点O引一条射线Ox，同时确定一个长度单位和计算角度的正方向(通常取逆时针方向)，这样就建立了一个极坐标系.点O称为极点，射线Ox称为极轴.平面内任一点M的位置可以由线段OM的长度ρ和从射线Ox到射线OM的角度θ来刻画(如图所示).这两个数组成的有序数对(ρ，θ)称为点M的极坐标.ρ称为点M的_____，θ称为点M的____.一般认为ρ≥0.当极角θ的取值范围是[0,2π)时，平面上的点(除去极点)就与极坐标(ρ，θ)(ρ≠0)建立一一对应的关系.我们设定，极点的极坐标中，极径ρ＝0，极角θ可取任意角.
(2)极坐标与直角坐标的互化设M为平面内的一点，它的直角坐标为(x，y)，极坐标为(ρ，θ).由图可知下面关系式成立：___________或______________，这就是极坐标与直角坐标的互化公式.
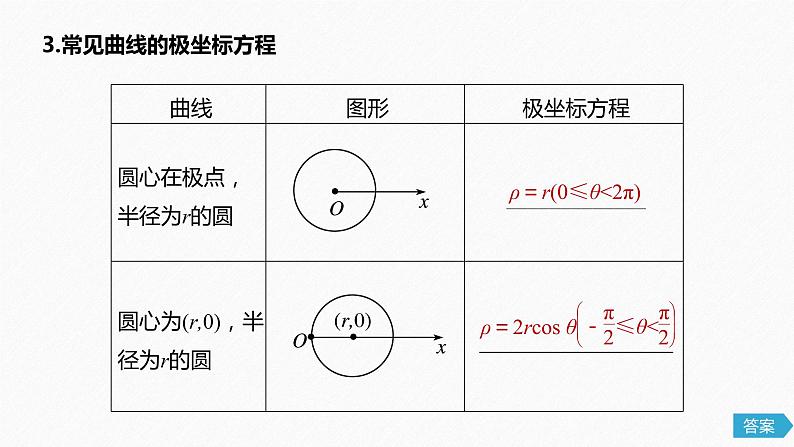
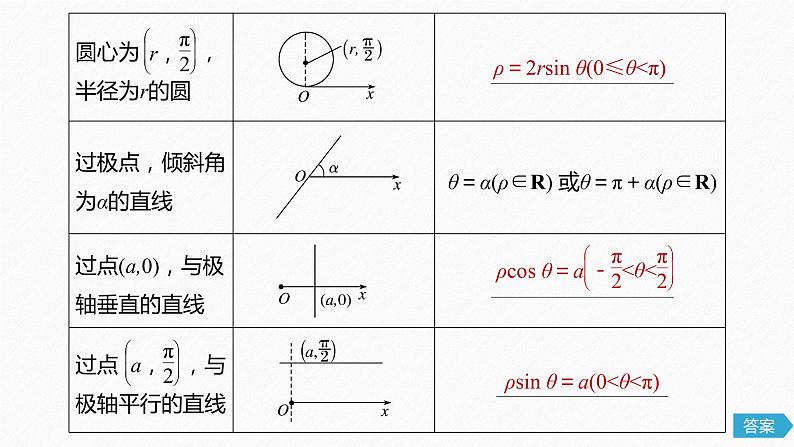
3.常见曲线的极坐标方程
ρ＝r(0≤θ0).
由|OM|·|OP|＝16，得C2的极坐标方程ρ＝4cs θ(ρ>0).因此C2的直角坐标方程为(x－2)2＋y2＝4(x≠0).
(2)设点A的极坐标为 ，点B在曲线C2上，求△OAB面积的最大值.
解　设点B的极坐标为(ρB，α)(ρB>0).由题设知|OA|＝2，ρB＝4cs α，
1.在以直角坐标系中的原点O为极点，x轴正半轴为极轴的极坐标系中，已知曲线的极坐标方程为ρ＝ .(1)将曲线的极坐标方程化为直角坐标方程；
∴曲线的直角坐标方程为x2＝4y＋4.
(2)过极点O作直线l交曲线于点P，Q，若|OP|＝3|OQ|，求直线l的极坐标方程.
解　设直线l的极坐标方程为θ＝θ0(ρ∈R)，
2.已知曲线C1的参数方程为 (t为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ＝4cs θ.(1)求曲线C1的极坐标方程和曲线C2的直角坐标方程；
两式相乘得x2－y2＝4.
即ρ2cs 2θ＝4，因为ρ＝4cs θ，所以ρ2＝4ρcs θ，则曲线C2的直角坐标方程为x2＋y2－4x＝0.
(2)若射线θ＝ 分别与曲线C1，C2交于A，B两点(异于极点)，求|AB|的值.
3.极坐标系与直角坐标系xOy有相同的长度单位，以坐标原点O为极点，以x轴正半轴为极轴.已知曲线C1的极坐标方程为 ，曲线C2的极坐标方程为ρsin θ＝a(a>0)，射线θ＝φ，θ＝φ＋ ，θ＝φ－ ，θ＝φ＋ 与曲线C1分别交异于极点O的四点A，B，C，D.(1)若曲线C1关于曲线C2对称，求a的值，并把曲线C1和C2化成直角坐标方程；
化为直角坐标方程为(x－1)2＋(y－1)2＝2.把C2的方程化为直角坐标方程为y＝a，因为曲线C1关于曲线C2对称，故直线y＝a经过圆心(1,1)，解得a＝1，故C2的直角坐标方程为y＝1.
(2)求|OA|·|OC|＋|OB|·|OD|的值.
所以|OA|·|OC|＋|OB|·|OD|
4.(2018·宁夏石嘴山第三中学模拟)在直角坐标系xOy中，圆C的参数方程为 (α为参数)，以O为极点，x轴的正半轴为极轴建立极坐标系，直线的极坐标方程为ρ(sin θ＋ cs θ)＝ .(1)求C的极坐标方程；
解　圆C的普通方程是(x－2)2＋y2＝4，又x＝ρcs θ，y＝ρsin θ，所以圆C的极坐标方程为ρ＝4cs θ.
(2)射线OM：θ＝θ1 与圆C的交点为O，P，与直线l的交点为Q，求|OP|·|OQ|的取值范围.
解　设P(ρ1，θ1)，则有ρ1＝4cs θ1，设Q(ρ2，θ1)，且直线l的极坐标方程是
所以2≤|OP||OQ|≤3.即|OP||OQ|的取值范围是[2,3].
5.(2018·广东广州仲元中学模拟)如图，在直角坐标系xOy中，曲线C1： (α为参数).以O为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ＝8cs θ，直线l的极坐标方程为θ＝ (ρ∈R).(1)求曲线C1的极坐标方程与直线l的直角坐标方程；
解　依题意得，曲线C1的普通方程为(x－2)2＋y2＝7，曲线C1的极坐标方程为ρ2－4ρcs θ－3＝0，
(2)若直线l与C1，C2在第一象限分别交于A，B两点，P为C2上的动点，求△PAB面积的最大值.
解　曲线C2的直角坐标方程为(x－4)2＋y2＝16，
6.在平面直角坐标系xOy中，曲线C1的参数方程为 (a>b>0，φ为参数)，在以O为极点，x轴的正半轴为极轴的极坐标系中，曲线C2是圆心在极轴上，且经过极点的圆.已知曲线C1上的点M 对应的参数φ＝ ，射线θ＝与曲线C2交于点D .(1)求曲线C1，C2的直角坐标方程；
设圆C2的半径为R，由题意，圆C2的极坐标方程为ρ＝2Rcs θ(或(x－R)2＋y2＝R2)，
即R＝1，所以曲线C2的极坐标方程为ρ＝2cs θ，所以曲线C2的直角坐标方程为(x－1)2＋y2＝1.