



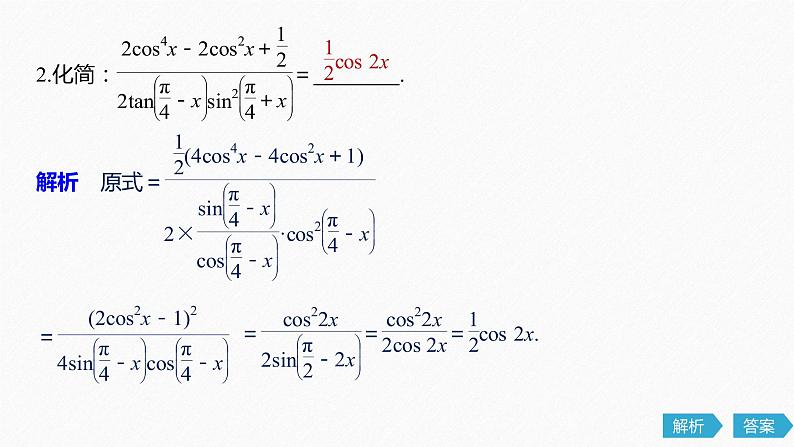



高中数学高考23第四章 三角函数、解三角形 4 5 简单的三角恒等变换 第2课时 简单的三角恒等变换课件PPT
展开NEIRONGSUOYIN
题型分类 深度剖析
题型一 三角函数式的化简
(1)三角函数式的化简要遵循“三看”原则一看角,二看名,三看式子结构与特征.(2)三角函数式的化简要注意观察条件中角之间的联系(和、差、倍、互余、互补等),寻找式子和三角函数公式之间的共同点.
题型二 三角函数的求值
(1)给角求值与给值求值问题的关键在“变角”,通过角之间的联系寻找转化方法.(2)给值求角问题:先求角的某一三角函数值,再求角的范围确定角.
则(2sin α-3cs α)·(sin α+cs α)=0,
∴2sin α=3cs α,又sin2α+cs2α=1,
题型三 三角恒等变换的应用
(2)求f(x)的最小正周期及单调递增区间.
解 由cs 2x=cs2x-sin2x与sin 2x=2sin xcs x,
所以f(x)的最小正周期是π.由正弦函数的性质,
三角恒等变换的应用策略(1)进行三角恒等变换要抓住:变角、变函数名称、变结构,尤其是角之间的关系;注意公式的逆用和变形使用.(2)把形如y=asin x+bcs x化为y= sin(x+φ),可进一步研究函数的周期性、单调性、最值与对称性.
讨论形如y=asin ωx+bcs ωx型函数的性质,一律化成y= sin(ωx+φ)型的函数;研究y=Asin(ωx+φ)型函数的最值、单调性,可将ωx+φ视为一个整体,换元后结合y=sin x的图象解决.
SIXIANGFANGFA
化归思想和整体代换思想在三角函数中的应用
(1)求f(x)的定义域与最小正周期;
6.若函数f(x)=5cs x+12sin x在x=θ时取得最小值,则cs θ等于
∴6tan α-6=1+tan α(tan α≠-1),∴tan α= .
解析 ∵cs4α-sin4α=(sin2α+cs2α)(cs2α-sin2α)
于是sin β=sin[α-(α-β)]=sin αcs(α-β)-cs αsin(α-β)
(1)求sin(α+π)的值;
由β=(α+β)-α,得cs β=cs(α+β)cs α+sin(α+β)sin α,
所以函数f(x)的最小正周期为π.
备战2024高考一轮复习数学(理) 第四章 三角函数与解三角形 第三节 第2课时 简单的三角恒等变换课件PPT: 这是一份备战2024高考一轮复习数学(理) 第四章 三角函数与解三角形 第三节 第2课时 简单的三角恒等变换课件PPT,共23页。
备战2024年高考总复习一轮(数学)第4章 三角函数、解三角形 第3节 第2课时 简单的三角恒等变换课件PPT: 这是一份备战2024年高考总复习一轮(数学)第4章 三角函数、解三角形 第3节 第2课时 简单的三角恒等变换课件PPT,共27页。PPT课件主要包含了研考点精准突破,考向1给角求值,答案A,考向2给值求值,考向3给值求角,答案C,答案D等内容,欢迎下载使用。
高中数学高考第3讲 第2课时 简单的三角恒等变换课件PPT: 这是一份高中数学高考第3讲 第2课时 简单的三角恒等变换课件PPT,共25页。PPT课件主要包含了word部分,点击进入链接等内容,欢迎下载使用。












