数学人教A版 (2019)8.6 空间直线、平面的垂直复习练习题

这是一份数学人教A版 (2019)8.6 空间直线、平面的垂直复习练习题，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
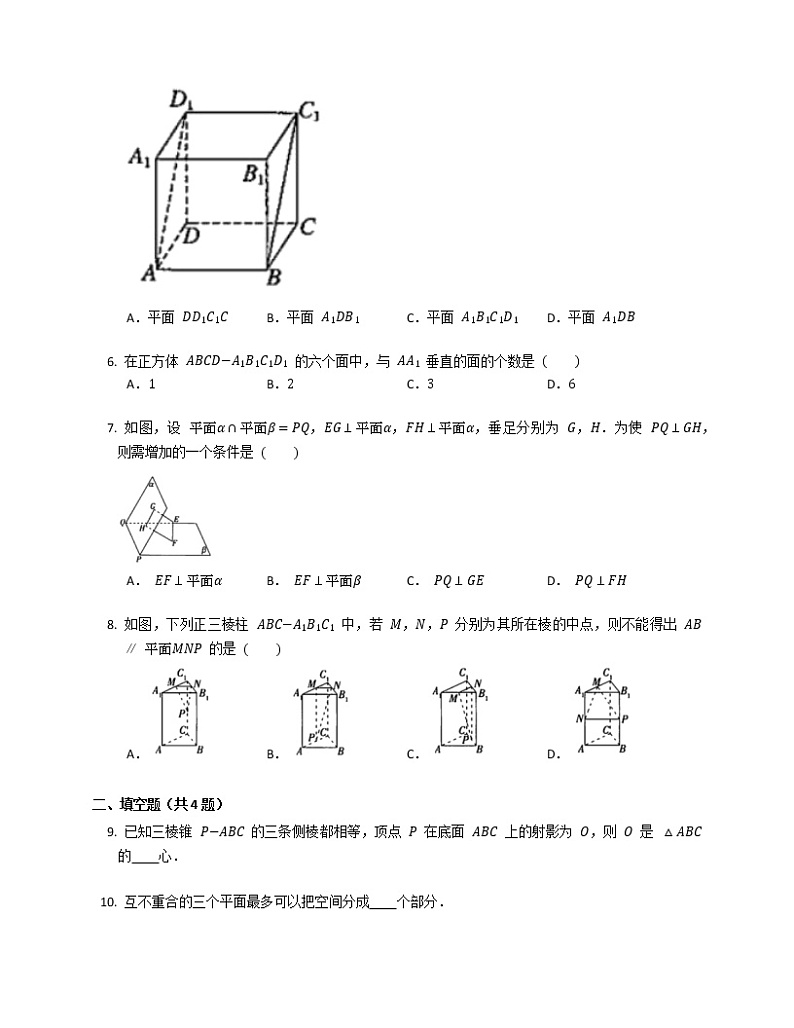
8.6空间直线、平面的垂直（共18题） 一、选择题（共8题）在正四面体 中，，， 分别是 ，， 的中点，下面四个结论中不成立的是  A．  B．  C．  D．  已知直线 ，，平面 ，，，，则 是 的  A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 如图，不同在一个平面内的三条平行直线和两个平行平面相交，两个平面内以交点为顶点的两个三角形是  A．相似但不全等的三角形 B．全等三角形 C．面积相等的不全等三角形 D．以上结论都不对 下列命题正确的是  ① ；② ；③ ． A．①② B．①③ C．②③ D．① 如图，在正方体 中，与 垂直的平面是  A．平面  B．平面  C．平面  D．平面  在正方体 的六个面中，与 垂直的面的个数是  A． B． C． D． 如图，设 ，，，垂足分别为 ，．为使 ，则需增加的一个条件是  A．  B．  C．  D．  如图，下列正三棱柱 中，若 ，， 分别为其所在棱的中点，则不能得出 的是  A． B． C． D． 二、填空题（共4题）已知三棱锥 的三条侧棱都相等，顶点 在底面 上的射影为 ，则 是 的    心． 互不重合的三个平面最多可以把空间分成    个部分． 如图，二面角 的大小是 ，线段 ，， 与 所成的角为 ，则 与平面 所成的角的正弦值是    ． 在四棱锥 中，底面 为正方形， 底面 ，，，， 分别是棱 ，， 的中点，对于平面 截四棱锥 所得的截面多边形，有以下三个结论：①截面的面积等于 ；②截面是一个五边形；③截面只与四棱锥 四条侧棱中的三条相交．其中，所有正确结论的序号是    ． 三、解答题（共6题）如图，在三棱锥 中，，， 为侧棱 上一点，它的正（主）视图和侧（左）视图如图所示．(1)  证明：；(2)  求三棱锥 的体积；(3)  在 的平分线上确定一点 ，使得 ，并求此时 的长． 如图，在直三棱柱 中，，，， 为 的中点．(1)  求证：；(2)  求异面直线 与 所成角的余弦值． 如图，已知三棱锥 ，，，，， 为 的中点，且 为正三角形．（）求证：；（）求三棱锥 的体积． 如图，在四棱锥 中，底面 为菱形，，，， 是 上任一点，．(1)  求证：；(2)  若 是 的中点，求 与平面 所成角的正弦值． 如图，在三棱柱 中，四边形 是边长为 的正方形，．再从条件①、条件②、条件③中选择两个能解决下面问题的条件作为已知，并作答．条件①：；条件②：；条件③：．(1)  求证：；(2)  求直线 与平面 所成角的正弦值． 如图，在四棱锥 中，底面 为菱形，，， 为线段 的中点， 为线段 上的一点．(1)  证明：平面 平面 ．(2)  若 ，二面角 的余弦值为 ，求 与平面 所成角的正弦值．
答案一、选择题（共8题）1.  【答案】C【解析】因为在正四面体 中，，， 分别是 ，， 的中点，所以 ，因为 ，，所以 ，故A正确；因为 ， 是 中点，所以 ，，因为 ，所以 ，因为 ，所以 ，故B正确；因为 ，，所以 ，因为 ，且 与平面 不垂直，所以平面 与平面 不垂直，故C错误；因为 ，且 ，所以 ，故D正确． 2.  【答案】A【解析】 ，，，反之若满足条件 ，，，平面也可以是 ． 3.  【答案】B【解析】由题意知 ，，由面面平行的性质定理，得 ，则四边形 为平行四边形，所以 ，同理 ，，所以 ． 4.  【答案】D 5.  【答案】B【解析】因为 ，，，，所以 ． 6.  【答案】B【解析】仅有平面 和平面 与直线 垂直． 7.  【答案】B【解析】因为 ，，所以 ．若 ，则由 ，得 ．又 与 为相交直线，所以 ，所以 ，故选B． 8.  【答案】C【解析】在A、B 选项中，易知 ，所以易证 ；在D选项中，易知 ，所以易证 ． 二、填空题（共4题）9.  【答案】外【解析】如图所示，因为顶点 在底面 上的射影为 ，所以 ．所以 ． ，，，因为 ．所以 ．所以 是 的外心． 10.  【答案】  11.  【答案】 【解析】如图，作 于 ， 于 ，连接 ，，则 ，则 为二面角 的平面角， 为 与 所成的角．设 与 所成的角为 ，则 ．由图象得 ． 12.  【答案】②③ 三、解答题（共6题）13.  【答案】(1)  因为 ，所以 ，又 ，所以 ，所以 ．由三视图可得，在 中，， 为 中点，所以 ，所以 ．(2)  由三视图可得 ，由（1）知 ，，又三棱锥 的体积即为三棱锥 的体积，所以所求三棱锥的体积 ．(3)  取 的中点 ，连接 并延长至 ，使得 ，点 即为所求．因为 为 中点，所以 ，因为 ，，所以 ，连接 ，，四边形 的对角线互相平分，所以 为平行四边形，所以 ，又 ，所以在直角 中，． 14.  【答案】(1)  因为 ，，，所以 ，，又 ，，所以 ，又因为 ，所以 ．(2)  如图，设 ，则 为 的中点，连接 ．因为 为 的中点，所以 ，因为 ，，所以 ．由 ， 为异面直线 与 所成的角，在 中，， ，， ，所以异面直线 与 所成角的余弦值为 ． 15.  【答案】（）因为 为 的中点且 为正三角形，所以 ，又因为 ，，所以 ，所以 ，又 ，且 ，所以 ．（）由（）得 ， ， ，且 ， ，由 为 的中点 ． 16.  【答案】(1)   ，底面 菱形，可得 ，又 ，又 ，， ，，， ，．(2)  若 是 的中点，连接 ，则 ，所以 ，， 两两垂直，建立如图所示的坐标系，不妨设 ，则 ，，，，设平面 的法向量为 ， 取 ，则 ，所以，，直线 的方向向量为 ， ．  与平面 所成角的正弦值为：． 17.  【答案】(1)  选择①②：因为 ，，，所以 ，即 ．又因为 ，，所以 ．选择①③．因为 ，，，所以 ．又因为 ， ，所以 ．(2)  由（）知 ，．因为四边形 是正方形，所以 ．如图，以 为坐标原点，以 ，， 所在的直线分别为 轴、 轴、 轴，建立空间直角坐标系 ，则 ，，，，，所以 ，，，设平面 的一个法向量为 ，则 即 令 ，则 ，，所以 ．设直线 与平面 所成的角为 ，则 ．所以直线 与平面 所成角的正弦值为 ． 18.  【答案】(1)  连接 ，因为 ， 为线段 的中点，所以 ．又 ，，所以 为等边三角形，．因为 ，所以 平面 ，又 ，所以平面 平面 ．(2)  设 ，则 ，因为 ，所以 ，同理可证 ，所以 平面 ．如图，设 ，以 为坐标原点， 的方向为 轴正方向，建立空间直角坐标系 ．易知 为二面角 的平面角，所以 ，从而 ．由 ，得 ．又由 ，，知 ，．设平面 的法向量为 ，由 ，，得 不妨设 ，得 ．又 ，，所以 ．设 与平面 所成角为 ，则 ．所以 与平面 所成角的正弦值为 ．