甘肃省陇南市校联考2022-2023学年七年级上学期期末考试数学试题（含详细答案）

甘肃省陇南市校联考2022-2023学年七年级上学期期末考试数学试题

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．数轴上点P表示的数为，与点P距离为3个单位长度的点表示的数为（　　）

A．1 B．5 C．1或﹣5 D．1或5

2．“一方有难，八方支援”，各省市都斥资到抗疫前线，据有关部门初步统计，国家已经投入资金1390亿元用于抗疫防控．将139000000000用科学记数法表示为（    ）

A． B． C． D．

3．下列有关整式的说法中，正确的是（    ）

A．是单项式 B．是三次四项式 C．系数是 D．没有常数项

4．教材中“整式的加减”一章的知识结构如图所示，则A和B分别代表的是（    ）

A．整式，合并同类项 B．单项式，合并同类项

C．系数，次数 D．多项式，合并同类项

5．下列计算正确的是（    ）

A． B．

C． D．

6．如图，小亮为将一个衣架固定在墙上，他在衣架两端各用一个钉子进行固定，用数学知识解释他这样操作的原因，应该是（    ）

A．过一点有无数条直线 B．两点之间线段的长度，叫做这两点之间的距离

C．两点确定一条直线 D．两点之间，线段最短

7．如图所示，点，，在同一直线上，若，则的度数为（    ）

A． B． C． D．

8．解方程，去分母正确的是（    ）

A． B．

C． D．

9．如图，把半径为1的圆放到数轴上，圆上一点A与表示的点重合，圆沿着数轴滚动一周，此时点A表示的数是（    ）

A． B．

C．或 D．或

10．《九章算术》中有这样一道数学问题，原文如下：清明游园，共坐八船，大船满六，小船满四，三十八学子，满船坐观．请问客家，大小几船？其大意为：清明时节出去游园，所有人共坐了只船，大船每只坐人，小船每只坐人，人刚好坐满，问：大小船各有几只？若设有只小船，则可列方程为（    ）

A． B．

C． D．

二、填空题

11．的相反数是___________．

12．“的2倍与5的和”用式子表示为______．

13．规定一种新运算“☆”对于任意两个有理数a和b，有a☆b＝a-b+1，请你根据新运算，计算（2☆3）☆2的值是___________

14．一个直角三角形绕其直角边旋转一周得到的几何体是_______．

15．若代数式的值为，则代数式的值为 _____．

16．“方程”二字最早见于我国《九章算术》这部经典著作中，该书的第八章名为“方程”如： 从左到右列出的算筹数分别表示方程中未知数，的系数与相应的常数项，即可表示方程，则 表示的方程是_______．

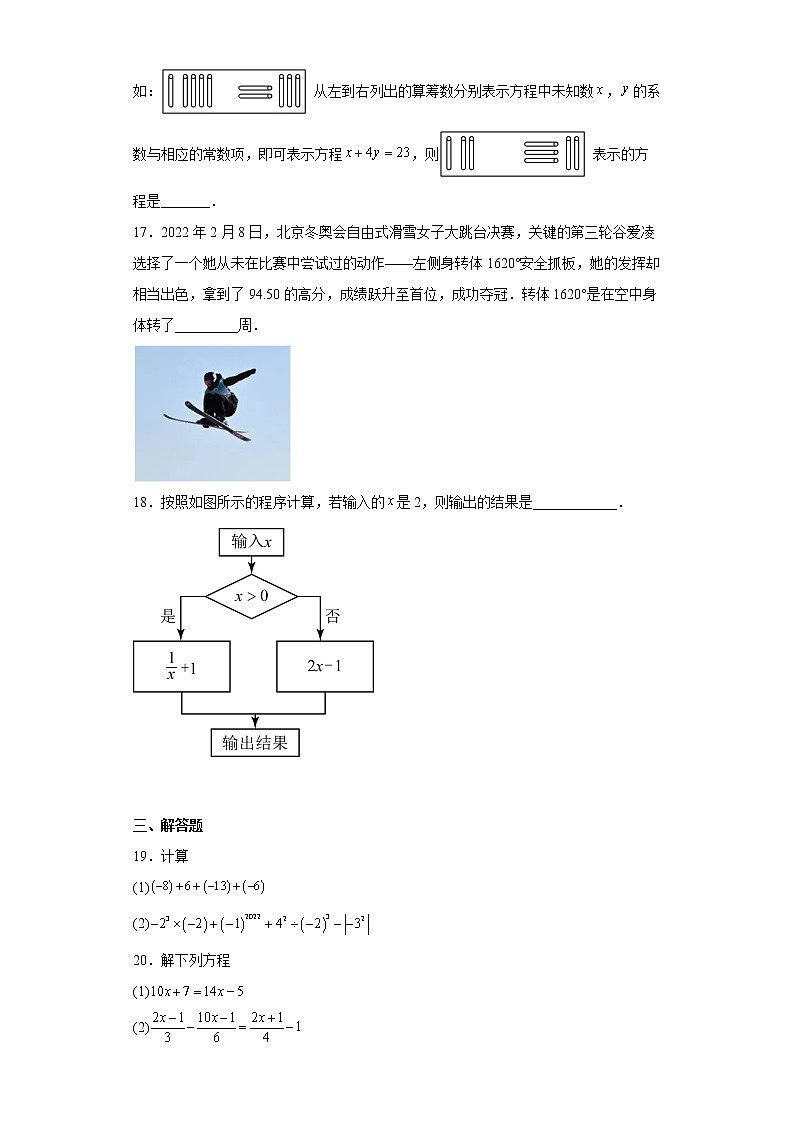
17．2022年2月8日，北京冬奥会自由式滑雪女子大跳台决赛，关键的第三轮谷爱凌选择了一个她从未在比赛中尝试过的动作——左侧身转体1620°安全抓板，她的发挥却相当出色，拿到了94.50的高分，成绩跃升至首位，成功夺冠．转体1620°是在空中身体转了_________周．

18．按照如图所示的程序计算，若输入的是2，则输出的结果是____________．

三、解答题

19．计算

(1)

(2)

20．解下列方程

(1)

(2)

21．如图是由8个相同的小立方体组成的几何体，请在下列方框内画出它的从三个方向所看到的平面图形（线条用黑色签字笔描黑）．

22．如图，O为直线DA上一点，OE是∠AOB的平分线，∠FOB＝90°．

(1)∠AOF的余角是　        ；

(2)∠DOB的补角是　       　；

(3)若∠EOF＝20°，求∠AOF的度数．

23．小明在计算多项式减去多项式时，误计算成加上这个多项式，结果得到答案．

(1)请你帮小明求出多项式；

(2)对于（1）中的多项式，当，时，求多项式的值．

24．出租车司机李师傅从上午在大厦至会展中心的东西走向路上营运．共连续运载十批乘客，若规定向东为正，向西为负，李师傅运载这十批乘客的里程如下（单位：千米）：．

(1)将最后一批乘客送到目的地时，李师傅在第一批乘客出发地的东边还是西边？相距多少千米？

(2)上午李师傅开车行驶的路程是多少？

25．【阅读材料】数学课上，老师给出了如下问题：如图1，一条直线上有四点，线段，点为线段的中点，线段，请你补全图形，并求的长．

以下是小华的解答过程：

解：如图2，

因为线段，点为线段的中点，

所以____________

因为，

所以______

小斌说：我觉得这个题应该有两种情况，小华只考虑了点在线段上，事实上，点还可以在线段的延长线上．

完成以下问题：

(1)请你将小华的解答过程补充完整；

(2)根据小斌的想法，请你在备用图中画出另一种情况对应的示意图，并求出此时的长．

26．2022年11月21日，万众嘱目的卡塔尔世界杯足球赛开幕，为了迎接世界杯足球赛的到来，足球协会举办了一次足球赛，其中得分规则及奖励方案如下表：

当比赛进行到每队比赛完12场时，A队共积分20分，并且没有负一场．

(1)试判断A队胜，平各几场？

(2)每赛一场，A队每名队员均得出场费500元，那么比赛完12场后，A队的某一名队员所得奖金与出场费累计为多少元？

27．为了节约水资源，某地区对居民用水实行阶梯水价制度，将居民全年用水量（取整数）划分为三档，标准如下

如该地某户全年用水量为250立方米．则其应缴全年综合水费（含水费、水资源费、污水处理费）合计为（元）

(1)如该地某户全年用水量为300立方米．则其应缴全年综合水费（含水费、水资源费、污水处理费）合计为多少元？

(2)如该地某户缴纳全年综合水费（含水费、水资源费、污水处理费）1180元，求该户全年用水量是多少立方米？

28．将一副三角板中含有角的三角板的顶点和另一块含有角的三角板的顶点重合于一点，绕着点旋转含有角的三角板，拼成如图的情况（在内部），请回答问题：

（1）如图1放置，将含有角的一边与角的一边重合，求出此时的度数；

（2）绕着点，转动三角板，恰好是平分，此时的度数应该是多少？

（3）是否存在这种情况，的度数恰好等于度数的3倍．如果存在，请求出的度数，如果不存在请说明理由．

参考答案：

1．C

【分析】在数轴上表示出P点，找到与点P距离3个长度单位的点所表示的数即可．此类题注意两种情况：要求的点可以在已知点的左侧或右侧．

【详解】解：如图：

根据数轴可以得到在数轴上与点P距离3个长度单位的点所表示的数是：或1，

故选：C．

【点睛】此题主要考查了数轴，用几何方法借助数轴来求解，非常直观，且不容易遗漏，体现了数形结合的优点．

2．D

【分析】根据科学记数法的表示方法求解即可．

【详解】．

故选：D．

【点睛】本题主要考查科学记数法．科学记数法的表示形式为的形式，其中，n为整数．解题关键是正确确定a的值以及n的值．

3．B

【分析】根据多项式的次数及项数定义解答．

【详解】解：是多项式，是三次四项式，常数项是，

∴A，C，D选项错误，B选项正确，

故选：B．

【点睛】此题考查了多项式次数及项数定义，熟记定义并正确解决问题是解题的关键．

4．D

【分析】根据整式的定义，整式的加减运算，即可得到答案

【详解】单项式和多项式统称为整式，整式的加减就是合并同类项，

∴A代表的是多项式，B代表的是合并同类项．

故选：D．

【点睛】本题考查了整式，单项式和多项式统称作整式，注意整式的加减就是合并同类项是解答本题的关键．

5．D

【分析】根据同类项定义、合并同类项法则、去括号法则逐一判断即可．

【详解】A. ，所以原式错误，此选项不符合题意；

B.-2(a+b)= -2a-2b， 所以原式错误，此选项不符合题意；

C.6xy与- x不是同类项，不能合并，此选项不符合题意；

D. ，此选项符合题意；

故选：D．

【点睛】本题主要考查整式的加减，解题的关键是掌握同类项定义、合并同类项法则、去括号法则．

6．C

【分析】这样操作的原因是：两点确定一条直线．

【详解】解：小亮这样操作的原因是：两点确定一条直线．

故选C．

【点睛】本题考查直线的性质．熟练掌握两点确定一条直线，是解题的关键．

7．A

【分析】利用余角补角的定义求解即可．

【详解】解：∵ ∠AOC=90° ， ∠1=28° ，

∴ ∠BOC=90°−28°=62° ，

∵ ∠2 与 ∠BOC 互为补角，

∴ ∠2=180°−62°=118° ，

故选：A．

【点睛】本题考查余角补角的定义，熟记补角定义是解题的关键，余角定义：如果两个角的和等于 90° ，则这两个角互为余角；补角的定义：如果两个角的和等于 180° ，则这两个角互为补角．

8．C

【分析】根据等式的性质去分母即可．

【详解】解：方程两边同时乘6得：．

故选：C．

【点睛】本题考查了解一元一次方程，解题关键是在解方程去分母时注意不要漏乘．

9．C

【分析】根两种情况讨论：当圆沿着数轴往右或往左滚动一周，所经过的路径长为圆的周长，据此解答．

【详解】解：圆滚动一周所经过的路径长为：

当圆沿着数轴往右滚动一周，此时点A表示的数是：-1+；

当圆沿着数轴往左滚动一周，此时点A表示的数是：，

综上所述，点A表示的数是或，

故选：C．

【点睛】本题考查数轴上的点，涉及圆的周长、分类讨论法等，是基础考点，掌握相关知识是解题关键．

10．A

【分析】一共是38人，设小船有x条，那么大船就有（8−x）条，用x分别表示出大船和小船坐的人数，进而列方程，即可求解．

【详解】解：设小船有x条，那么大船就有（8−x）条，

由题意得：，

故选A．

【点睛】本题主要考查一元一次方程的实际应用，找出等量关系，列出方程，是解题的关键．

11．

【分析】先化简多重符号，再根据相反数的定义进行求解即可．

【详解】解：的相反数是，

故答案为：．

【点睛】本题主要考查了化简多重符号，求一个数的相反数，熟知只有符号不同的两个数互为相反数，0的相反数是0是解题的关键．

12．##

【分析】根据题意列出代数式，即可求解．

【详解】解：依题意得，

故答案为：．

【点睛】本题考查了列代数式，理解题意是解题的关键．

13．

【分析】先按照新定义计算括号内的运算，得到括号内的结果后再利用新定义法则进行运算即可．

【详解】解： a☆b＝a-b+1，

（2☆3）☆2

☆2

0☆2

故答案为：

【点睛】本题考查的是新定义运算，有理数的加减运算，理解题意，列出正确的运算式是解本题的关键．

14．圆锥

【分析】根据面动成体，可得答案．

【详解】以直角三角形的一条直角边所在直线为对称轴旋转一周，得到一个圆锥，

故答案为：圆锥．

【点睛】题考查了点、线、面、体，点动成线，线动成面，面动成体：以直角三角形的一条直角边所在直线为对称轴旋转一周得到圆锥．

15．

【分析】根据题意得出，整体代入即可求解．

【详解】解：∵代数式的值为，即，

∴

，

故答案为：．

【点睛】本题考查了代数式求值，整体代入是解题的关键．

16．

【分析】根据横着的算筹为10，竖放的算筹为1，依次表示的系数与等式后面的数字，即可求解．

【详解】解： 表示的方程是

故答案为：

【点睛】本题考查了列二元一次方程组，理解题意是解题的关键．

17．4.5

【分析】根据题意用1620°除以360°求解即可．

【详解】解：，

∴转体1620°是在空中身体转了4.5周

故答案为：4.5．

【点睛】此题考查了有理数的除法运算的实际应用，解题的关键是熟练掌握有理数的除法运算法则．

18．##1.5

【分析】由，则直接把代入中计算即可．

【详解】解：∵

∴当时，．

故答案为：．

【点睛】本题主要考查了流程图、代数式求值等知识点，根据流程图和x的取值，正确列出代数式是解答本题的关键．

19．(1)

(2)6

【分析】（1）先利用加法交换律和结合律进行变形，然后根据有理数的加法法则计算即可；

（2）按照先算乘方、再算乘除、最后算加减的顺序计算即可．

【详解】（1）解：

=

=

=；

（2）解：

=

=

=6．

【点睛】本题考查了有理数的混合运算，掌握有理数的加法法则，交换律、结合律，乘方法则，乘除法则，绝对值的意义等知识是解题的关键．

20．(1)

(2)

【分析】（1）根据移项、合并同类项、未知数的系数化为1的步骤求解即可．

（2）根据去分母、去括号、移项、合并同类项、未知数的系数化为1的步骤求解即可．

【详解】（1）解：，

，

，

．

（2）解：，

，

，

，

，

．

【点睛】本题考查了一元一次方程的解法，熟练掌握一元一次方程的解题步骤是解答本题的关键．

21．见解析

【分析】根据题意可知，主视图有3列，每列小正方形的数目分别为3，1，2；左视图有2列，每列小正方形的数目分别为3，1；俯视图有3列，每列小正方形的数目分别为2，2，1．

【详解】解：

从正面看                从左面看              从上面看

【点睛】本题主要考查了简单组合体的三视图，解题关键是通过观察组合体依次分析三视图的情况．

22．(1)∠BOD

(2)∠AOB

(3)50°

【分析】（1）根据平角定义可得∠AOF+∠BOD＝90°，再根据余角定义可得答案；

（2）根据如果两个角的和等于180°（平角），就说这两个角互为补角．即其中一个角是另一个角的补角可得答案；

（3）首先计算出∠BOE的度数，进而可得∠AOE的度数，再根据角的和差关系可得答案．

【详解】（1）∵∠BOF＝90°，

∴∠AOF+∠BOD＝180°﹣90°＝90°，

∴∠AOF的余角是∠BOD，

故答案为：∠BOD；

（2）∠DOB的补角是∠AOB，

故答案为：∠AOB；

（3）∵∠EOF＝20°，∠FOB＝90°，

∴∠BOE＝70°，

∵OE是∠AOB的平分线，

∴∠AOE＝∠BOE＝70°，

∵∠EOF＝20°，

∴∠AOF＝50°．

【点睛】此题主要考查了余角和补角，以及角的计算，关键是掌握余角：如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角．补角：如果两个角的和等于180°（平角），就说这两个角互为补角．即其中一个角是另一个角的补角．

23．(1)

(2)

【分析】（1）根据整式的加减进行计算即可；

（2）直接代值计算即可．

【详解】（1）解：由题意，得

；

（2）当，时，

．

【点睛】本题考查整式的加减及代数式的求值，解题关键是正确地进行整式的加减．

24．(1)东边，相距6千米

(2)54千米

【分析】（1）约定向东为正方向，正数表示向东，负数表示向西，所有数据相加即可求解．

（2）所有数据的绝对值相加即可解得．

【详解】（1）

（千米）．

答：将最后一批乘客送到目的地时，李师傅在第一批乘客出发地的东边，相距6千米．

（2）（千米）．

答：上午李师傅开车行驶的路程是54千米．

【点睛】此题考查了有理数的混合运算在实际问题中的应用，解题的关键是正确理解题意，根据题意列式解决问题．

25．(1)见解析

(2)图见解析，

【分析】（1）根据是的中点，即可得到与的数量关系，若在线段上时，根据和的长即可求得的长；

（2）根据是的中点，即可得到与的数量关系，若在射线上时，根据和的长即可求得的长．

【详解】（1）∵线段，点C为线段的中点，

∴；

∵，

当在线段上时，

∴；

（2）如图，当点在射线上时，

∵线段，点C为线段的中点，

∴，

∵，

∴．

【点睛】本题考查了线段的性质、线段的和差等知识，解题的关键是读懂题意，分情况讨论．

26．(1)A队胜4场，平8场

(2)17600元

【分析】（1）根据题意找出等量关系式列出方程即可解得．

（2）由（1）可得，根据题意列式计算可得．

【详解】（1）解：设A队胜利x场，

∵一共打了12场，

∴平了场，

∴，

解得：，

（场）．

答：A队胜4场，平8场．

（2）∵每场比赛出场费500元，

∴12场比赛出场费共6000元，

又∵赢了4场，奖金为（元），

平了8场，奖金为（元），

∴ （元）．

答：A队的某一名队员所得奖金与出场费累计为17600元．

【点睛】此题考查了一元一次方程的应用，解题的关键是根据题意找出等量关系式列出方程．

27．(1)全年综合水费为元；

(2)该户全年用水量是立方米．

【分析】（1）根据题意可得，该地某户全年用水量为300立方米，处在第三阶梯，分别求出一、二、三阶梯的水费，即可求解；

（2）首先确定该户处于第几阶段，再设该户全年用水量是立方米，列方程求解即可．

【详解】（1）解：∵，

∴该地某户水费处在第三阶梯，

则全年综合水费为（元），

答：全年综合水费为元；

（2）解：第一阶段水费最高为：（元）

第二阶段水费最高为：（元）

∵

∴该地某户水费处在第二阶梯，

设该户全年用水量是立方米，

由题意可得：，

解得，

答：该户全年用水量是立方米．

【点睛】此题考查了一元一次方程的应用，有理数运算的应用，解题的关键是理解题意，正确列出方程或式子．

28．（1）∠AOD的度数为；（2）∠AOD的度数为；（3）存在，∠AOD的度数为．

【分析】(1)根据题意，由所给三角板即可得到结论；

(2)根据角平分线的定义得到∠BOD=∠COD=22.5°，于是得到结论；

(3)设∠BOC=x，然后表示出∠AOC和∠BOD，再列出方程求解即可．

【详解】(1)由三角板知，∠AOB=60°，∠COD=45°，

∠AOD=45°+60=105°；

(2)OB平分∠COD，

∠BOD=∠COD =× 45°= 22.5°；

∠AOD=∠AOB+∠BOD

=60°+22.5°=82.5°；

(3)设∠BOC=x，

则∠AOC=60°-x，∠BOD=45°-x，

∠AOC=3∠BOD，

60°-x=3 (45°-x），

解得x=37.5°，

此时，∠AOD=∠COD+∠AOC=45°+（60°-37.5°）

=45°+22.5°=67.5°．

【点睛】本题考查了三角形的内角和，角平分线的定义，正确的识别图形是解题的关键．