高中数学高考2018高考数学（文）大一轮复习习题 板块命题点专练（十五） Word版含答案

 www.ks5u.com板块命题点专练（十五）

1．(2016·全国丙卷)执行如图所示的程序框图，如果输入的a＝4，b＝6，那么输出的n＝(　　)

A．3　　　　　　　 B．4

C．5  D．6

解析：选B　程序运行如下：

开始a＝4，b＝6，n＝0，s＝0．

第1次循环：a＝2，b＝4，a＝6，s＝6，n＝1；

第2次循环：a＝－2，b＝6，a＝4，s＝10，n＝2；

第3次循环：a＝2，b＝4，a＝6，s＝16，n＝3；

第4次循环：a＝－2，b＝6，a＝4，s＝20，n＝4．

此时，满足条件s>16，退出循环，输出n＝4．故选B．

2．(2015·全国卷Ⅱ)下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的a，b分别为14,18，则输出的a＝(　　)

A．0  B．2

C．4  D．14

解析：选B　a＝14，b＝18．

第一次循环：14≠18且14<18，b＝18－14＝4；

第二次循环：14≠4且14>4，a＝14－4＝10；

第三次循环：10≠4且10>4，a＝10－4＝6；

第四次循环：6≠4且6>4，a＝6－4＝2；

第五次循环：2≠4且2<4，b＝4－2＝2；

第六次循环：a＝b＝2，跳出循环，输出a＝2，故选B．

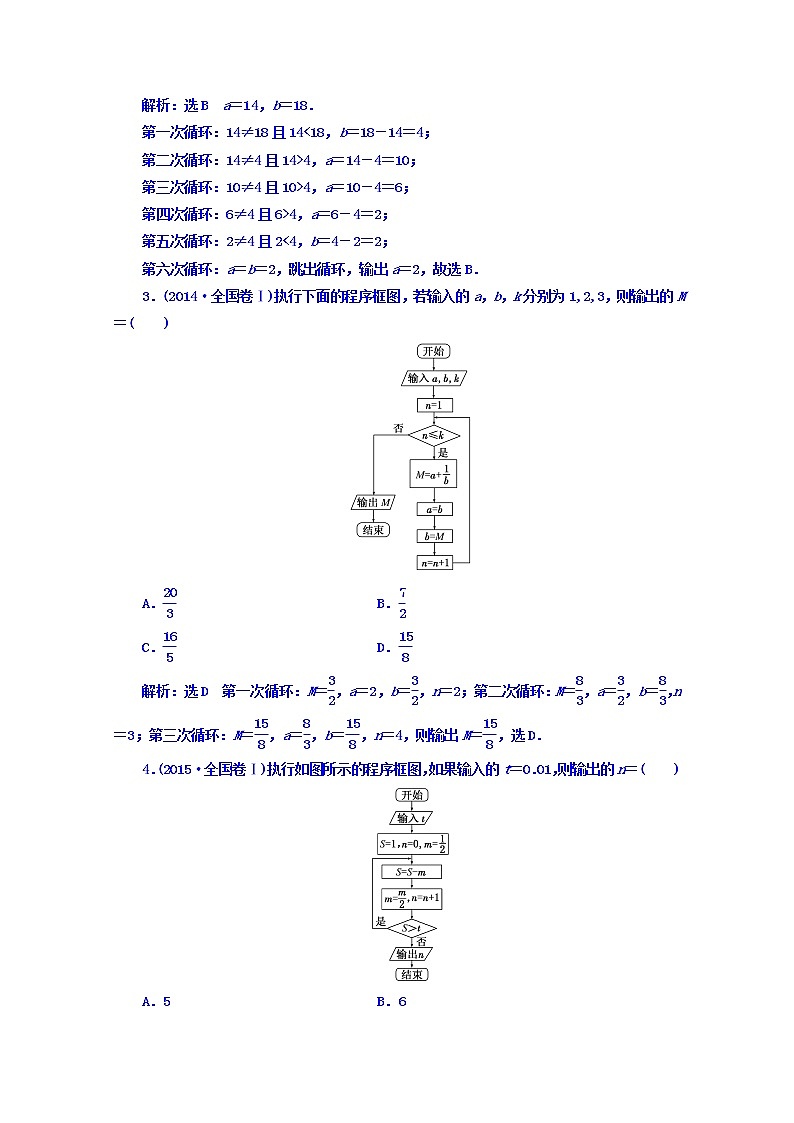
3．(2014·全国卷Ⅰ)执行下面的程序框图，若输入的a，b，k分别为1,2,3，则输出的M＝(　　)

A．　　　　　　　　　　 B．

C．  D．

解析：选D　第一次循环：M＝，a＝2，b＝，n＝2；第二次循环：M＝，a＝，b＝，n＝3；第三次循环：M＝，a＝，b＝，n＝4，则输出M＝，选D．

4．(2015·全国卷Ⅰ)执行如图所示的程序框图，如果输入的t＝0．01，则输出的n＝(　　)

A．5  B．6

C．7  D．8

解析：选C　运行第一次：S＝1－＝＝0．5，m＝0．25，n＝1，S>0．01；

运行第二次：S＝0．5－0．25＝0．25，m＝0．125，n＝2，S>0．01；

运行第三次：S＝0．25－0．125＝0．125，m＝0．062 5，n＝3，S>0．01；

运行第四次：S＝0．125－0．062 5＝0．062 5，m＝0．031 25，n＝4，S>0．01；

运行第五次：S＝0．031 25，m＝0．015 625，n＝5，S>0．01；

运行第六次：S＝0．015 625，m＝0．007 812 5，n＝6，S>0．01；

运行第七次：S＝0．007 812 5，m＝0．003 906 25，n＝7，S<0．01．

输出n＝7．故选C．

1．(2015·四川高考)某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异，拟从这三个年级中按人数比例抽取部分学生进行调查，则最合理的抽样方法是(　　)

A．抽签法　　　　　　　 B．系统抽样法

C．分层抽样法  D．随机数法

解析：选C　根据年级不同产生差异及按人数比例抽取易知应为分层抽样法．

2．(2015·北京高考)某校老年、中年和青年教师的人数见下表，采用分层抽样的方法调查教师的身体状况，在抽取的样本中，青年教师有320人，则该样本中的老年教师人数为(　　)

A．90  B．100

C．180  D．300

解析：选C　设该样本中的老年教师人数为x，由题意及分层抽样的特点得＝，故x＝180．

1．(2014·四川高考)在“世界读书日”前夕，为了了解某地5 000 名居民某天的阅读时间，从中抽取了200名居民的阅读时间进行统计分析．在这个问题中，5 000名居民的阅读时间的全体是(　　)

A．总体  B．个体

C．样本的容量  D．从总体中抽取的一个样本

解析：选A　5 000名居民的阅读时间的全体是总体，每名居民的阅读时间是个体，200是样本容量，故选A．

2．(2015·重庆高考)重庆市2013年各月的平均气温(℃)数据的茎叶图如下图，则这组数据的中位数是(　　)

A．19  B．20

C．21．5  D．23

解析：选B　由茎叶图可知这组数据由小到大依次为8,9,12,15,18,20,20,23,23,28,31,32，所以中位数为＝20．

3．(2015·广东高考)某工厂36名工人的年龄数据如下表．

(1)用系统抽样法从36名工人中抽取容量为9的样本，且在第一分段里用随机抽样法抽到的年龄数据为44，列出样本的年龄数据；

(2)计算(1)中样本的均值和方差s2；

(3)36名工人中年龄在－s与＋s之间有多少人？所占的百分比是多少(精确到0．01%)?

解：(1)由系统抽样的知识可知，36人分成9组，每组4人，其中第一组的工人年龄为44，所以其编号为2，故所有样本数据的编号为4n－2，n＝1,2，…，9．其数据为：44,40,36,43,36,37,44,43,37．

(2)＝＝40．

由方差公式知，s2＝＝．

(3)因为s2＝，所以s＝∈(3,4)，

所以36名工人中年龄在－s和＋s之间的人数等于在区间内的人数，即40,40,41，…，39，共23人．

所以36名工人中年龄在－s和＋s之间的人数所占的百分比为≈63．89%．

4．(2016全国乙卷)某公司计划购买1台机器，该种机器使用三年后即被淘汰．机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元．在机器使用期间，如果备件不足再购买，则每个500元．现在决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：

记x表示1台机器在三年作用期内需更换的易损零件数，y表示1台机器在购买易损零件上所需的费用(单位：元)，n表示购机的同时购买的易损零件数．

(1)若n＝19，求y与x的函数解析式；

(2)若要求“需更换的易损零件数不大于n”的频率不小于0．5，求n的最小值；

(3)假设这100台机器在购机的同时每台都购买19个易损零件，或每台都购买20个易损零件，分别计算这100台机器在购买易损零件上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买19个还是20个易损零件？

解：(1)当x≤19时，y＝3 800；

当x＞19时，y＝3 800＋500(x－19)＝500x－5 700，

所以y与x的函数解析式为

y＝(x∈N)．

(2)由柱状图知，需更换的零件数不大于18的频率为0．46，不大于19的频率为0．7，故n的最小值为19．

(3)若每台机器在购机同时都购买19个易损零件，则这100台机器中有70台在购买易损零件上的费用为3 800,20台的费用为4 300,10台的费用为4 800，因此这100台机器在购买易损零件上所需费用的平均数为(3 800×70＋4 300×20＋4 800×10)＝4 000．

若每台机器在购机同时都购买20个易损零件，则这100台机器中有90台在购买易损零件上的费用为4 000,10台的费用为4 500，因此这100台机器在购买易损零件上所需费用的平均数为 (4 000×90＋4 500×10)＝4 050．

比较两个平均数可知，购买一台机器的同时应购买19个易损零件．

1．(2015·福建高考)为了解某社区居民的家庭年收入与年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：

根据上表可得回归直线方程＝x＋，其中＝0．76，＝－．据此估计，该社区一户年收入为15万元家庭的年支出为(　　)

A．11．4万元  B．11．8万元

C．12．0万元  D．12．2万元

解析：选B　由题意知，＝＝10，

＝＝8，

∴＝8－0．76×10＝0．4，

∴当x＝15时，＝0．76×15＋0．4＝11．8(万元)．

2．(2015·全国卷Ⅰ)某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x(单位：千元)对年销售量y(单位：t)和年利润z(单位：千元)的影响．对近8年的年宣传费xi和年销售量yi(i＝1,2，…，8)数据作了初步处理，得到下面的散点图及一些统计量的值．

表中wi＝，＝i．

(1)根据散点图判断，y＝a＋bx与y＝c＋d哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？(给出判断即可，不必说明理由)

(2)根据(1)的判断结果及表中数据，建立y关于x的回归方程；

(3)已知这种产品的年利润z与x，y的关系为z＝0．2y－x．根据(2)的结果回答下列问题：

①年宣传费x＝49时，年销售量及年利润的预报值是多少？

②年宣传费x为何值时，年利润的预报值最大？

附：对于一组数据(u1，v1)，(u2，v2)，…，(un，vn)，其回归直线v＝α＋βu的斜率和截距的最小二乘估计分别为＝，＝－ ．

解：(1)由散点图可以判断，y＝c＋d适宜作为年销售量y关于年宣传费x的回归方程类型．

(2)令w＝，先建立y关于w的线性回归方程．

由于＝＝＝68，

＝－＝563－68×6．8＝100．6，

所以y关于w的线性回归方程为＝100．6＋68w，

因此y关于x的回归方程为＝100．6＋68．

(3)①由(2)知，当x＝49时，

年销售量y的预报值＝100．6＋68＝576．6，

年利润z的预报值＝576．6×0．2－49＝66．32．

②根据(2)的结果知，年利润z的预报值

＝0．2(100．6＋68)－x＝－x＋13．6＋20．12．

所以当＝＝6．8，即x＝46．24时，取得最大值．

故年宣传费为46．24千元时，年利润的预报值最大．