2023年中考数学一轮复习《与圆有关的计算》基础巩固练习(含答案)

这是一份2023年中考数学一轮复习《与圆有关的计算》基础巩固练习(含答案)，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
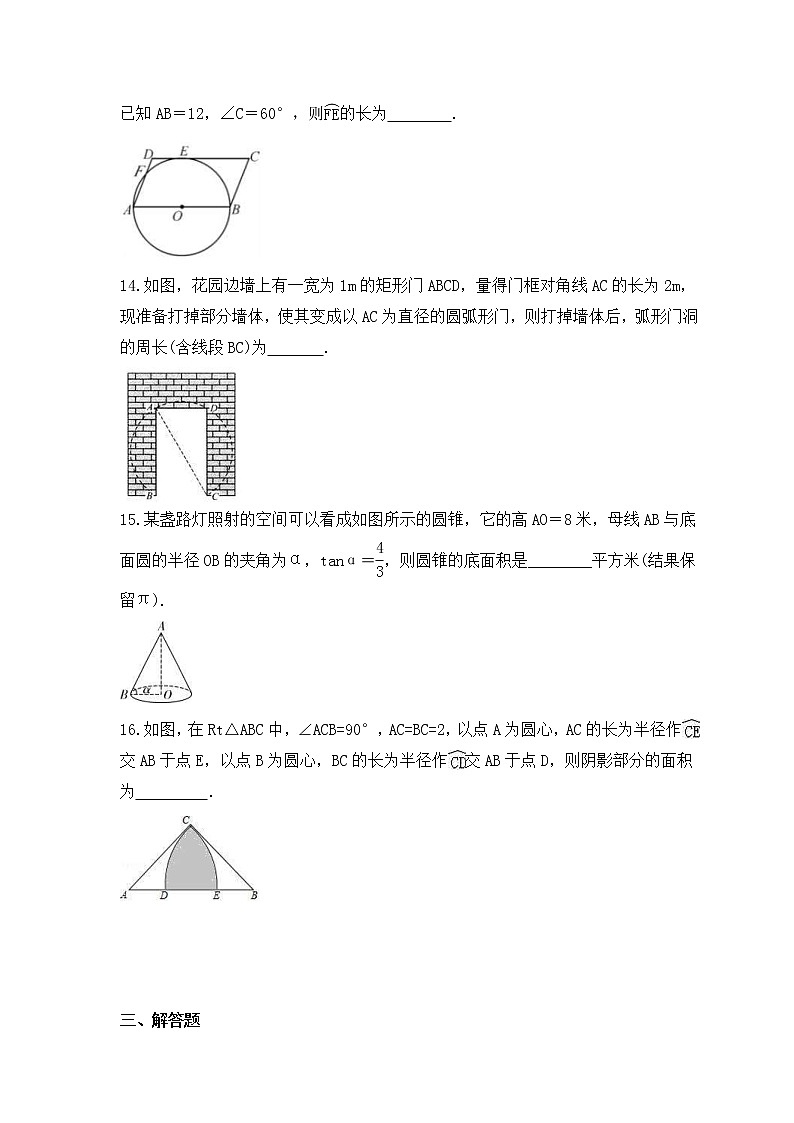
2023年中考数学一轮复习《与圆有关的计算》基础巩固练习一              、选择题1.如图所示，正六边形ABCDEF内接于⊙O，则∠ADB的度数是(　　)A.60°　        B.45°         C.30°　      D.22.5°2.正三角形内切圆半径r与外接圆半径R之间的关系为(        )A.4R=5r       B.3R=4r          C.2R=3r          D.R=2r3.如果一个四边形的外接圆与内切圆是同心圆，那么这个四边形一定是(　　)A.矩形         B.菱形          C.正方形        D.不能确定4.若扇形的半径为6，圆心角为120°，则此扇形的弧长是(　　)A.3π         B.4π         C.5π          D.6π5.如图，在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型.若圆的半径为r，扇形的半径为R，扇形的圆心角等于90°，则R与r之间的关系是(    ).A.R=2r         B.           C.R=3r            D.R=4r6.如图，AB 为⊙O 的切线，切点为 B，连接 AO 与⊙O 交与点 C，BD 为⊙O 的直径，连接 CD，若∠A＝30°，OA＝2，则图中阴影部分的面积为(     )A.﹣        B.π﹣2      C.π﹣      D.π﹣7.如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为（    ）A.30πcm2                   B.48πcm2                         C.60πcm2                            D.80πcm28.一个圆锥的侧面积是底面积的2倍，则该圆锥侧面展开图的圆心角的度数是(　　)A.120°         B.180°         C.240°         D.300°9.“赶陀螺”是一项深受人们喜爱的运动，如图所示是一个陀螺的立体结构图，已知底面圆的直径AB＝8 cm，圆柱体部分的高BC＝6 cm，圆锥体部分的高CD＝3 cm，则这个陀螺的表面积是(　　)A.68π cm2      B.74π cm2      C.84π cm2     D.100π cm210.如图①是半径为2的半圆，点C是弧AB的中点，现将半圆如图②方式翻折，使得点C与圆心O重合，则图中阴影部分的面积是(　　)A.π         B.π﹣         C.2＋         D.2﹣二              、填空题11.正八边形的中心角等于________度.12.如图，正六边形ABCDEF内接于半径为4的圆，则B、E两点间的距离为　   　． 13.如图，在▱ABCD中，AB为⊙O的直径，⊙O与DC相切于点E，与AD相交于点F，已知AB＝12，∠C＝60°，则的长为        .14.如图，花园边墙上有一宽为1m的矩形门ABCD，量得门框对角线AC的长为2m，现准备打掉部分墙体，使其变成以AC为直径的圆弧形门，则打掉墙体后，弧形门洞的周长(含线段BC)为　   　.15.某盏路灯照射的空间可以看成如图所示的圆锥，它的高AO＝8米，母线AB与底面圆的半径OB的夹角为α，tanα＝，则圆锥的底面积是________平方米(结果保留π).16.如图，在Rt△ABC中，∠ACB=90°，AC=BC=2，以点A为圆心，AC的长为半径作交AB于点E，以点B为圆心，BC的长为半径作交AB于点D，则阴影部分的面积为　   　．   三              、解答题17.如图，正方形ABCD内接于⊙O，M为中点，连结BM、CM.(1)求证：BM=CM；(2)当⊙O的半径为2时，求的长.     18.如图，在△ABC中，AB＝AC，∠BAC＝54°，以AB为直径的⊙O分别交AC，BC于点D，E，过点B作⊙O的切线，交AC的延长线于点F.(1)求证：BE＝CE；(2)求∠CBF的度数；(3)若AB＝6，求弧AD的长.      19.如图，Rt△ABC中，∠C=90°，AC=，tanB=.半径为2的⊙C，分别交AC，BC于点D，E，得到.(1)求证：AB为⊙C的切线；(2)求图中阴影部分的面积.           20.如图，在Rt△ABC中，∠C=90°，AC=5 cm，BC=12 cm，以BC边所在的直线为轴，将△ABC旋转一周得到一个圆锥，求这个圆锥的侧面积.           21.如图，⊙O是△ABC的外接圆，BC为⊙O的直径，点E为△ABC的内心，连接AE并延长交⊙O于D点，连接BD并延长至F，使得BD＝DF，连接CF、BE.(1)求证：DB＝DE；    (2)求证：直线CF为⊙O的切线.    (3)若CF＝4，求图中阴影部分的面积.
参考答案1.C.2.D3.C.4.B5.D6.A.7.C8.B.9.C.10.D.11.答案为：4512.答案为：8．13.答案为：π.14.答案为：(＋1)m.15.答案为：36π.16.答案为：π﹣2．17.(1)证明：∵四边形ABCD是正方形，∴AB=CD，∴=.∵M为中点，∴=，∴＋=＋，即=，∴BM=CM.　(2)解：∵⊙O的半径为2，∴⊙O的周长为4π.∵===，∴=＋=，∴的长=× ×4π=×4π=π. 18.证明：(1)连接AE，∵AB是⊙O直径，∴∠AEB＝90°，即AE⊥BC，∵AB＝AC，∴BE＝CE.(2)∵∠BAC＝54°，AB＝AC，∴∠ABC＝63°，∵BF是⊙O切线，∴∠ABF＝90°，∴∠CBF＝∠ABF﹣∠ABC＝27°.(3)连接OD，∵OA＝OD，∠BAC＝54°，∴∠AOD＝72°，∵AB＝6，∴OA＝3，∴弧AD的长是π.19.解：(1)如图，过点C作CF⊥AB于点F，在Rt△ABC中，tanB==，∴BC=2AC=2，∴AB===5，∴CF===2.∴AB为⊙C的切线；(2)S阴影=S△ABC－S扇形ECD=AC·BC－=××2－=5－π.20.解：∠C=90°，AC=5 cm，BC=12 cm，由勾股定理，得AB=13 cm.以BC边所在的直线为轴，将△ABC旋转一周，则所得到的几何体的底面圆周长为2π×5=10π(cm)，侧面积为×10π×13=65π(cm2).21.证明：(1)∵E是△ABC的内心，∴∠BAE＝∠CAE，∠EBA＝∠EBC，∵∠BED＝∠BAE＋∠EBA，∠DBE＝∠EBC＋∠DBC，∠DBC＝∠EAC，∴∠DBE＝∠DEB，∴DB＝DE
(2)证明：连接CD.

∵DA平分∠BAC，∴∠DAB＝∠DAC，∴ ，∴BD＝CD，∵BD＝DF，∴CD＝DB＝DF，∴∠BCF＝90°，∴BC⊥CF，∴CF是⊙O的切线.  连接OD.∵O、D是BC、BF的中点，CF＝4，∴OD＝2，∵∠BCF＝90°，∴∠BOD＝90°，∴图中阴影部分的面积＝扇形BOD的面积﹣△BOD的面积＝π﹣2.