北师大版高中数学必修第二册4-2两角和与差的三角函数公式第1课时课件

这是一份北师大版高中数学必修第二册4-2两角和与差的三角函数公式第1课时课件，共23页。

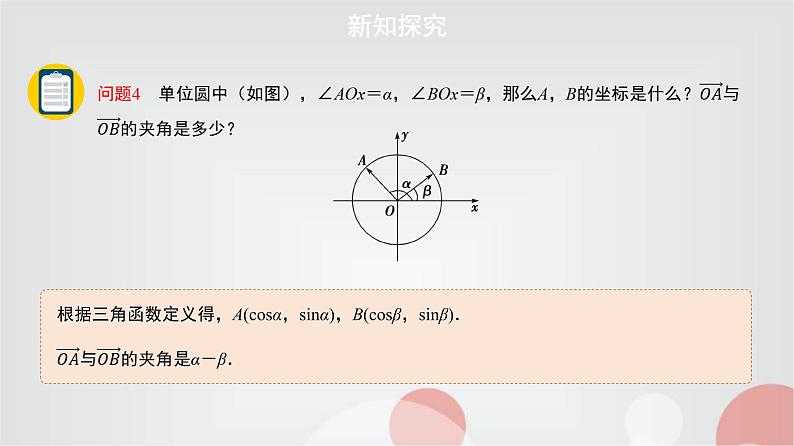
两角和与差的三角函数公式第1课时新知探究问题1　如图，为世界著名的艺术殿堂——法国卢浮宫，它的正门入口处有一个金字塔建筑，它的设计者就是著名的美籍华人建筑师贝聿铭．那么在测量这类建筑物的高度时（如右图），我们需要来解复合角∠DAC＝α－β的正、余弦值，这就需要对两角差的正、余弦进行变换．新知探究问题2　如何用角α，β的正弦、余弦值来表示cos(α－β)呢？有人认为cos(α－β)＝cosα－cosβ，你认为正确吗？试举出两例加以说明．不一定正确．新知探究问题3　计算下列各式子的值，并根据这些式子的共同特征，写出一个猜想．猜想：cosαcosβ＋sinαsinβ＝cos(α－β)．①cos45°cos45°＋sin45°sin45°＝1；③cos30°cos120°＋sin30°sin120°＝0．新知探究根据三角函数定义得，A(cosα，sinα)，B(cosβ，sinβ)．  新知探究   根据数量积相等，得 cos(α－β)＝cosαcosβ＋sinαsinβ．新知探究两角差的余弦公式cos（α－β）＝cos αcos β＋sin αsin β，记作Cα－β．新知探究①同名函数相乘：即两角余弦乘余弦，正弦乘正弦；公式中的α，β都是任意角，可以为常量，也可以为变角．②将所得的积相加．新知探究问题5　把公式cos(α－β)＝cosαcosβ＋sinαsinβ中的β用－β代替，结果如何？新知探究两角和的余弦公式Cos(α＋β)＝cosαcosβ－sinαsinβ．记作Cα＋β．新知探究余余正正，符号相反．因为15°＝60°－45°，所以可用两角差的余弦公式求解．例1　已知sinα＋sinβ＝ ，cosα＋cosβ＝ ，求cos(α－β)的值．初步应用由①＋②得：1＋1＋2(sinαsinβ＋cosαcosβ)＝1，即2cos(α－β)＝－1，  初步应用给条件求值问题要注意公式的正用、逆用，尤其是公式的逆用，要求能正确地找出所给式子与公式右边的异同，并积极创造条件逆用公式．方法总结例2　已知cosα＝ ，sin(α＋β)＝ ，且α，β均为锐角，求β的值．初步应用  又α，β为锐角，∴α＋β∈(0，π)．初步应用在解决此类题目时，一定要注意已知角与所求角之间的关系，恰当地运用拆角、拼角技巧，同时分析角之间的关系，利用角的代换化异角为同角．方法总结归纳小结（1）已知某些角的三角函数值，求另外一些角的三角函数值时，要注意什么？（2）给值求角的关键是什么？常用的角的变换技巧有哪些？问题6　回归本节的学习，你有什么收获？可以从以下几个问题归纳．（1）要注意观察已知角与所求表达式中角的关系，即拆角与凑角．（2）关键是变角，把所求角用含已知角的式子表示；互余或互补关系的应用；作业布置作业：教科书第152页，A组第1（1）（3）题，2（2），第3题．1目标检测Acos27°cos57°－sin27°cos147°等于（　　）A．C．D．B．    解析：原式＝cos27°cos57°－sin27°cos(180°－33°)＝cos27°cos57°＋sin27°cos33°＝cos(57°－27°)＝cos27°cos57°＋sin27°sin57°＝cos30°2目标检测若角α，β均为锐角，sin α＝ ，cos（α＋β）＝ ，则cos β＝（　　）A．C．D．B．      2目标检测A若角α，β均为锐角，sinα＝ ，cos(α＋β)＝ ，则cos β＝（　　）A．C．D．B．      ∴cosβ＝cos[(α＋β)－α]  ＝cos(α＋β)cosα＋sin(α＋β)sinα3目标检测 已知α，β∈[0， ]，sinα＝ ，cosβ＝ ，则cos(α＋β)＝________．   4目标检测已知sinα　　　　　　　　　　　　　　　 ，β是第三象限角，求：（1）cosα与sinβ的值． （2）cos(α－β)．4目标检测已知sin α　　　　　　　　　　　　　　　 ，β是第三象限角，求：（1）cos α与sin β的值． （2）cos（α－β）．（2）由（1）可得，  cos（α－β）＝cos αcos β＋sin αsin β＝右边．故原等式成立．