






北师大版 (2019)必修 第二册6.3 球的表面积和体积教学演示课件ppt
展开问题1 从生活经验中我们知道,不能将橘子皮展成平面,因为橘子皮近似于球面,这种曲面不能展成平面图形.
那么,人们又是怎样计算球面的面积的呢?古人在计算圆周率时,一般是用割圆术,即用圆的内接或外切正多边形来逼近圆的周长.理论上,只要取得圆内接正多边形的边数越多,圆周率越精确,直到无穷.这种思想就是朴素的极限思想.
运用上述思想能否计算球的表面积和体积?
极限思想可以用来计算球的表面积和体积.
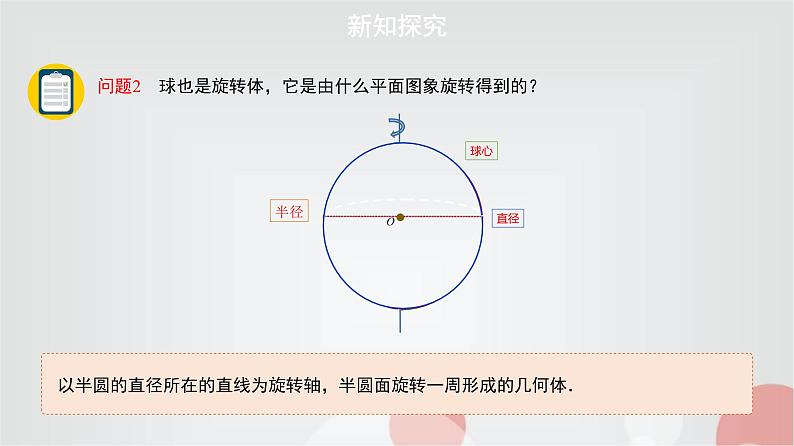
问题2 球也是旋转体,它是由什么平面图象旋转得到的?
以半圆的直径所在的直线为旋转轴,半圆面旋转一周形成的几何体.
问题3 用一个平面去截球体,截面的形状是什么?该截面的几何量与球的半径之间有什么关系?
可以想象,用一个平面去截球体,截面是圆面,
在球的轴截面图中,截面圆与球的轴截面的关系如图所示.
若球的半径为R,截面圆的半径为r,OO′=d.
在Rt△OO′C中,OC2=OO′2+O′C2,即R2=r2+d2.
问题4 过球外一点作球的切线,有几条?这些切线是什么关系?
过球外一点,有无数条切线,
问题5 阅读教材,填写下面的空格.
(1)球面被经过球心的平面截得的圆叫作球的________.
(2)被不经过球心的平面截得的圆叫作球的________.
(3)设截面圆的半径为r,球心到截面的距离为d,球的半径为R,则r=___________.
(1)当直线与球有唯一交点时,称直线与球______,其中它们的交点称为直线与球的切点.
(2)过球外一点,有无数条切线,所有切线的长度相等.这些切点的集合是以O′为圆心的圆,圆面O′及所有切线围成了______.
3.球的表面积和体积公式
(1)设球的半径为R,球的表面积为S球面=______;
(2)设球的半径为R,则球的体积V球=______.
问题6 球的表面积和球的大圆的面积之间有什么关系?
球面的面积(也就是球的表面积)等于它的大圆面积的4倍
例1 如图所示,一个圆锥形的空杯子上面放着一个半球形的冰激凌,如果冰激凌融化了,会溢出来吗?(假设冰激凌融化前后体积不变)
由于V半球<V圆锥,所以冰淇凌融化了,不会溢出杯子.
例2 一个圆柱形的玻璃瓶的内半径为3 cm,瓶里所装的水深为8 cm,将一个钢球完全浸入水中,瓶中水的高度上升到8.5,求钢球的半径.
解析:设钢球半径为R,由题意得:
所以钢球的半径为1.5cm.
练习:教科书第244页练习第1题,第2题.
(1)求球的体积与表面积的方法是什么?
(2)解决有关球的问题时,常用哪些性质?
问题3 本节课我们学习了球的表面积、体积的计算公式,请你通过下列问题,归纳所学知识.
(1)求球的体积与表面积的方法:
①要求球的体积或表面积,必须知道半径R或者通过条件能求出半径R,
然后代入体积或表面积公式求解.
②半径和球心是球的最关键要素,把握住了这两个要素,
计算球的表面积或体积的相关题目也就易如反掌了.
(2)解决有关球的问题时,常用以下性质:
①用任意平面截球所得的截面是一个圆面,球心和截面圆圆心的连线与这个截面垂直.
②如果分别用R和r表示球的半径和截面圆的半径,用d表示球心到截面的距离,
则R2=r2+d2.球的有关计算问题,常归结为解直角三角形.
作业:教科书第244页A组第1题,第4题.
若以球的球心为圆心,以球的半径为半径的圆的周长为c,则这个球的表面积为( )
解析:设球的半径为R,则2πR=c,
解析:由于正方体的体积为8,故正方体的棱长a为2.
又正方体的体对角线是其外接球的一条直径,
圆柱形容器内盛有高度为8cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是________cm.
解析:设球的半径为xcm,
2020-2021学年第八章 立体几何初步8.3 简单几何体的表面积与体积说课课件ppt: 这是一份2020-2021学年第八章 立体几何初步8.3 简单几何体的表面积与体积说课课件ppt,文件包含832圆柱圆锥圆台球的表面积和体积pptx、832分层演练综合提升docx等2份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
高中数学北师大版 (2019)必修 第二册6.3 球的表面积和体积教案配套课件ppt: 这是一份高中数学北师大版 (2019)必修 第二册6.3 球的表面积和体积教案配套课件ppt,文件包含63球的表面积和体积课件pptx、63球的表面积和体积docx等2份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
《球的表面积和体积》人教版高中数学必修二PPT课件: 这是一份高中数学人教版新课标A必修2本册综合教学演示课件ppt,共18页。PPT课件主要包含了祖暅原理,新知探究,球的体积公式的推导,球的体积计算公式,球的表面积公式,半球形物体的表面积为,随堂练习,正视图,侧视图,俯视图等内容,欢迎下载使用。













