




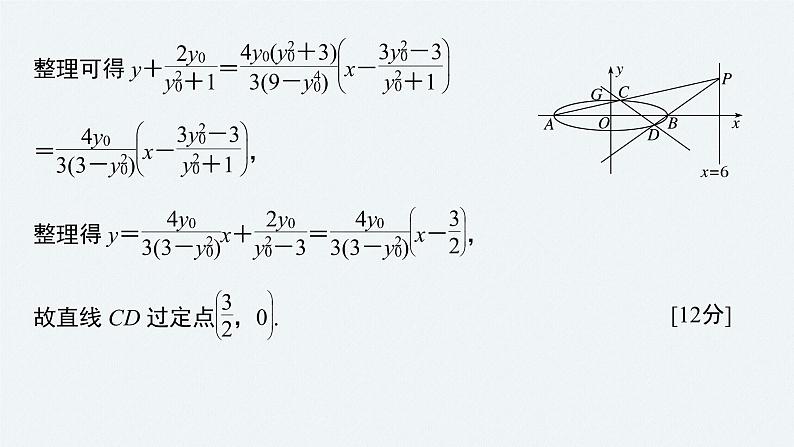


高中数学高考2022届高考数学一轮复习(新高考版) 第8章 高考专题突破五 第2课时 定点与定值问题课件PPT
展开
这是一份高中数学高考2022届高考数学一轮复习(新高考版) 第8章 高考专题突破五 第2课时 定点与定值问题课件PPT,共53页。PPT课件主要包含了答题模板,题型一定点问题,规范解答,∴直线CD的方程为,12分,题型二定值问题,1求C的方程,将①代入上式,课时精练,解得a=2等内容,欢迎下载使用。
例1 (12分)(2020·全国Ⅰ)已知A,B分别为椭圆E: +y2=1(a>1)的左、右顶点,G为E的上顶点, =8.P为直线x=6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.(1)求E的方程;(2)证明:直线CD过定点.
(1)解 依据题意作图,如图所示,
A(-a,0),B(a,0),G(0,1),
(2)证明 设P(6,y0),
第一步:确定曲线方程(一般根据待定系数法或定义法).第二步:设直线方程并与曲线方程联立,得关于x或y的一元二次方程.第三步:写出根与系数的关系(或求出交点坐标).第四步:将第三步得出的关系代入题目条件,解决范围、最值或定点、定值等问题.第五步:反思回顾,考虑方程有解条件和图形完备性.
跟踪训练1 (2019·北京)已知抛物线C:x2=-2py经过点(2,-1).(1)求抛物线C的方程及其准线方程;
解 由抛物线C:x2=-2py经过点(2,-1),得p=2.所以抛物线C的方程为x2=-4y,其准线方程为y=1.
(2)设O为原点,过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M,N,直线y=-1分别交直线OM,ON于点A和点B.求证:以AB为直径的圆经过y轴上的两个定点.
证明 抛物线C的焦点为F(0,-1).设直线l的方程为y=kx-1(k≠0).
Δ=16k2+16>0恒成立.设M(x1,y1),N(x2,y2),则x1x2=-4.
综上,以AB为直径的圆经过y轴上的定点(0,1)和(0,-3).
解得a2=6,b2=3.
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.
证明 设M(x1,y1),N(x2,y2).若直线MN与x轴不垂直,
得(1+2k2)x2+4kmx+2m2-6=0.
故(x1-2)(x2-2)+(y1-1)(y2-1)=0,整理得(k2+1)x1x2+(km-k-2)(x1+x2)+(m-1)2+4=0.
整理得(2k+3m+1)(2k+m-1)=0.因为A(2,1)不在直线MN上,所以2k+m-1≠0,所以2k+3m+1=0,k≠1.
若直线MN与x轴垂直,可得N(x1,-y1).
得(x1-2)(x1-2)+(y1-1)(-y1-1)=0.
若D与P不重合,则由题设知AP是Rt△ADP的斜边,
圆锥曲线中的定值问题的常见类型及解题策略(1)求代数式为定值.依题意设条件,得出与代数式参数有关的等式,代入代数式、化简即可得出定值.(2)求点到直线的距离为定值.利用点到直线的距离公式得出距离的解析式,再利用题设条件化简、变形求得.(3)求某线段长度为定值.利用长度公式求得解析式,再依据条件对解析式进行化简、变形即可求得.
(1)求椭圆C的方程;
(2)设椭圆C的左、右顶点分别为A1,A2,过A1,A2分别作x轴的垂线l1,l2,椭圆C的一条切线l:y=kx+m与l1,l2分别交于M,N两点,求证:∠MF1N为定值.
证明 由题意可知,l1的方程为x=-3,l2的方程为x=3.直线l分别与直线l1,l2的方程联立得M(-3,-3k+m),N(3,3k+m),
得(9k2+8)x2+18kmx+9m2-72=0.因为直线l与椭圆C相切,所以Δ=(18km)2-4(9k2+8)(9m2-72)=0,
化简得m2=9k2+8.
KESHIJINGLIAN
(1)求椭圆C的标准方程;
解 由椭圆的定义,可知
(2)过点B(4,0)作一条斜率不为0的直线l与椭圆C相交于P,Q两点,记点P关于x轴对称的点为P′.证明:直线P′Q经过x轴上一定点D,并求出定点D的坐标.
证明 由题意,设直线l的方程为x=my+4(m≠0).设P(x1,y1),Q(x2,y2),则P′(x1,-y1).
可得(m2+4)y2+8my+12=0.∵Δ=16(m2-12)>0,∴m2>12.
∴D(1,0).∴直线P′Q经过x轴上定点D,其坐标为(1,0).
2.(2020·西安模拟)设F1,F2为椭圆C: =1(b>0)的左、右焦点,M为椭圆上一点,满足MF1⊥MF2,已知△MF1F2的面积为1.(1)求椭圆C的方程;
解 由椭圆定义得|MF1|+|MF2|=4,①由MF1⊥MF2得|MF1|2+|MF2|2=|F1F2|2=4(4-b2),②
由①②③,可得b2=1,
(2)设C的上顶点为H,过点(2,-1)的直线与椭圆交于R,S两点(异于H),求证:直线HR和HS的斜率之和为定值,并求出这个定值.
解 依题意,H(0,1),显然直线RS的斜率存在且不为0,设直线RS的方程为y=kx+m(k≠0),代入椭圆方程并化简得(4k2+1)x2+8kmx+4m2-4=0.由题意知,Δ=16(4k2-m2+1)>0,设R(x1,y1),S(x2,y2),x1x2≠0,
∵直线RS过点(2,-1),∴2k+m=-1,∴kHR+kHS=-1.故kHR+kHS为定值-1.
3.(2018·北京)已知抛物线C:y2=2px经过点P(1,2),过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.(1)求直线l的斜率的取值范围;
解 因为抛物线y2=2px过点(1,2),所以2p=4,即p=2.故抛物线C的方程为y2=4x.由题意知,直线l的斜率存在且不为0.设直线l的方程为y=kx+1(k≠0),
依题意知Δ=(2k-4)2-4×k2×1>0,解得k
相关课件
这是一份2024年高考数学一轮复习专题六第2课时定点、定值、探究性问题课件,共41页。PPT课件主要包含了题型一定点问题,互动探究,题型二定值问题,题型三探究性问题,出条件,维采取另外的途径等内容,欢迎下载使用。
这是一份2024年高考数学一轮复习(新高考版) 第8章 §8.12 圆锥曲线中定点与定值问题课件PPT,共53页。PPT课件主要包含了题型一,定点问题,思维升华,题型二,定值问题,即为曲线C的方程,课时精练,基础保分练,1求C的方程,令y=0等内容,欢迎下载使用。
这是一份高中数学高考第8讲 第2课时 圆锥曲线中的定值、定点与存在性问题课件PPT,共34页。PPT课件主要包含了word部分,点击进入链接等内容,欢迎下载使用。








