高中数学高考板块2 核心考点突破拿高分 专题3 规范答题示例3课件PPT

这是一份高中数学高考板块2 核心考点突破拿高分 专题3 规范答题示例3课件PPT，共14页。PPT课件主要包含了审题路线图，构建答题模板等内容，欢迎下载使用。

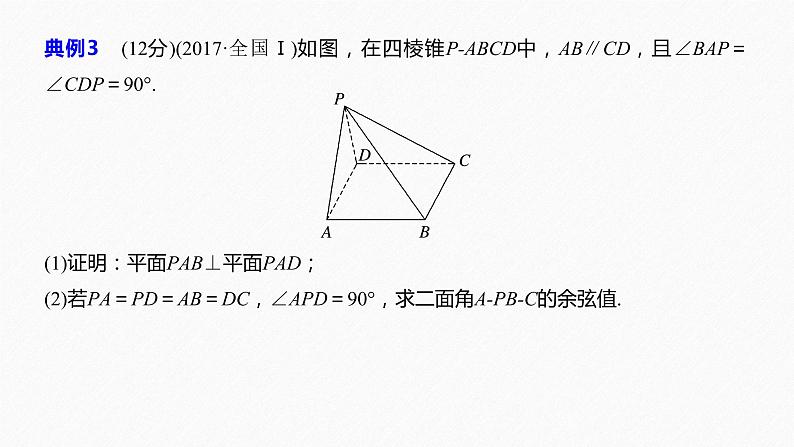
典例3　(12分)(2017·全国Ⅰ)如图，在四棱锥P-ABCD中，AB∥CD，且∠BAP＝∠CDP＝90°.(1)证明：平面PAB⊥平面PAD；(2)若PA＝PD＝AB＝DC，∠APD＝90°，求二面角A-PB-C的余弦值.
计算平面PCB与平面PAB的法向量→计算两个法向量的夹角的余弦值→求得二面角的余弦值.
规范解答 · 分步得分
(1)证明　由已知∠BAP＝∠CDP＝90°，得AB⊥AP，CD⊥PD.由于AB∥CD，故AB⊥PD，又PD∩PA＝P，PD，PA⊂平面PAD，所以AB⊥平面PAD. ………………………………………………………………2分又AB⊂平面PAB，…………………………………………………………………3分所以平面PAB⊥平面PAD.…………………………………………………………4分
(2)解　在平面PAD内作PF⊥AD，垂足为点F，由(1)知，AB⊥平面PAD，故AB⊥PF，可得PF⊥平面ABCD.
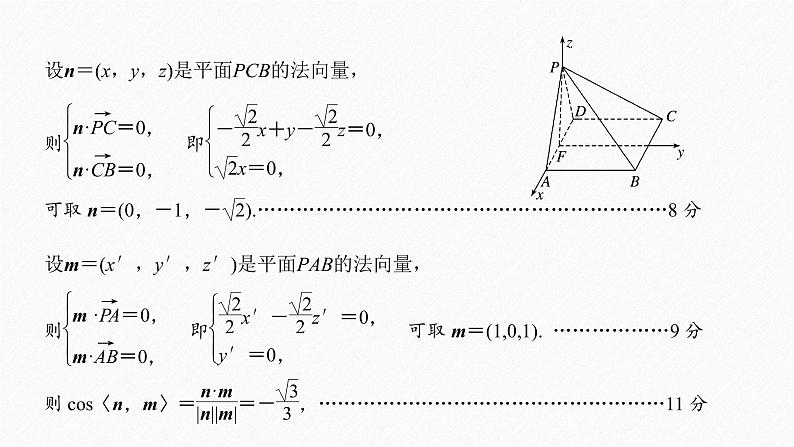
设n＝(x，y，z)是平面PCB的法向量，
设m＝(x′，y′，z′)是平面PAB的法向量，
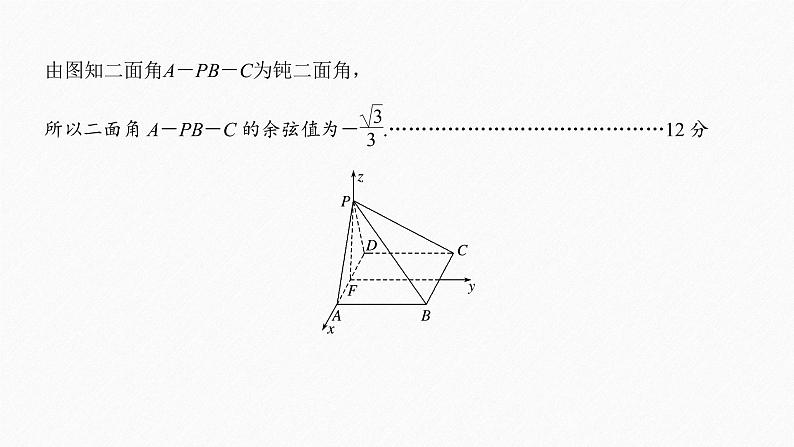
由图知二面角A－PB－C为钝二面角，
第一步 找垂直：找出(或作出)具有公共交点的两条直线，寻求与它们有垂直关系 的直线，由线面垂直得出面面垂直.第二步 写坐标：选择恰当的坐标原点，建立空间直角坐标系，写出点坐标.第三步 求向量：求两个平面的法向量.第四步 求夹角：运用夹角的余弦公式代入数值，计算向量的夹角.第五步 得结论：得到要求两个平面所成的角.
评分细则　第(1)问：证得AB⊥平面PAD得2分，直接写出不得分；写出AB⊂平面PAB得1分，此步没有扣1分；写出结论平面PAB⊥平面PAD得1分.第(2)问：正确建立空间直角坐标系得2分；写出相应的坐标及向量得1分(酌情)；正确求出平面PCB的法向量得1分；正确求出平面PAB的法向量得1分；写出公式cs〈n，m〉＝ 得1分，正确求出值再得1分；写出正确结果得1分.
跟踪演练3　(2018·全国Ⅰ)如图，四边形ABCD为正方形，E，F分别为AD，BC的中点，以DF为折痕把△DFC折起，使点C到达点P的位置，且PF⊥BF.(1)证明：平面PEF⊥平面ABFD；
证明　由已知可得BF⊥PF，BF⊥EF，PF∩EF＝F，PF，EF⊂平面PEF，所以BF⊥平面PEF.又BF⊂平面ABFD，所以平面PEF⊥平面ABFD.
(2)求DP与平面ABFD所成角的正弦值.
解　如图，作PH⊥EF，垂足为H.由(1)得，PH⊥平面ABFD.
建立如图所示的空间直角坐标系H－xyz.由(1)可得，DE⊥PE.
又PF＝1，EF＝2，所以PE⊥PF.
设DP与平面ABFD所成的角为θ，