北师大版高中数学必修第二册第1章3弧度制课件

这是一份北师大版高中数学必修第二册第1章3弧度制课件，共27页。

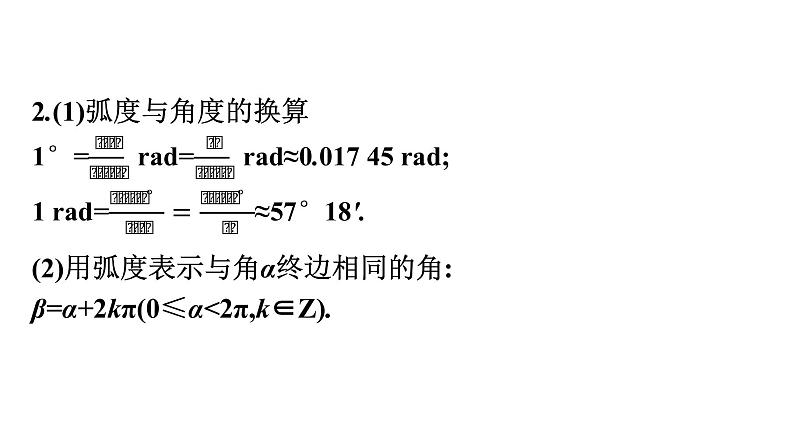
第一章　三角函数§3　弧度制自主预习·新知导学合作探究·释疑解惑易 错 辨 析 自主预习·新知导学一、弧度制【问题思考】1.在初中学过的角度制中,1度的角是如何规定的?2.在给定半径的圆中,弧长一定时,圆心角确定吗?提示:确定.3.度量角的两种单位制表1-3-14.(多选题)下列说法正确的是(　　). A.“度”与“弧度”是度量角的两种不同的度量单位B.在单位圆中,每一段弧的长度等于它所对圆心角的弧度数C.角的正负由角的旋转方向决定D.用角度制和弧度制度量角,都与圆的半径有关解析:根据1度、1弧度的定义可知只有D错,故选ABC.答案:ABC二、弧度与角度的换算【问题思考】1.角度制和弧度制都是度量角的单位制,它们之间如何进行换算呢?提示:利用1弧度角的定义进行换算,2.(1)弧度与角度的换算 (2)用弧度表示与角α终边相同的角:β=α+2kπ(0≤α<2π,k∈Z).(3)一些特殊角的角度数与弧度数的对应表表1-3-23.想一想:某同学表示与30°角终边相同的角的集合时写成S={α|α=2kπ+30°,k∈Z},这种表示正确吗?为什么?提示:这种表示不正确,在同一个式子中,角度、弧度不能混用,三、弧长公式【问题思考】1.初中所学的扇形的弧长公式是什么?能用弧度表示吗?提示:初中所学的扇形的弧长公式是l= (其中R是扇形的半径,n为其圆心角的角度数).能用弧度表示.因为α= ·2π,所以l=|α|R(其中α为其圆心角的弧度数).2.圆心角的弧度数公式:|α|= ,即圆心角的弧度数的绝对值等于该角所对的弧长与半径之比.3.知识拓展设扇形的半径为R,弧长为l,其圆心角为α,则表1-3-34.在半径为10的圆中,240°的圆心角所对的弧长为(　　)答案:A 合作探究·释疑解惑探究一探究二【例1】 如图1-3-1,用弧度制表示顶点在原点,始边与x轴的非负半轴重合,终边落在阴影部分内的角的集合.反思感悟 根据已知图形写出区域角的集合的步骤:(1)仔细观察图形;(2)写出区间边界对应的角;(3)用不等式表示区域范围内的角.注意事项:用不等式表示区域角的范围时,要注意角的集合形式是否能够合并,这一点容易出错.【例2】 (1)《九章算术》是中国古代的数学名著,其中《方田》一章给出了弧田面积的计算方法.1.将本例(2)中的条件“4”改为“10”,“1”改为“4”,其他条件不变,求扇形圆心角的弧度数.2.(变结论)将本例(2)中的条件“面积是1 cm2”删掉,扇形周长改为60 cm,求扇形OAB的最大面积及此时弧AB的长.解:设弧AB的长为l cm,半径为r cm,圆心角的弧度数为α,由已知l+2r=60,反思感悟 弧度制下解决扇形相关问题的步骤:(1)明确弧长公式和扇形的面积公式;(2)分析题目的已知量和待求量,灵活选择公式;(3)根据已知条件列方程(组)或建立目标函数求解.提醒:看清角的度量制,灵活选择公式.解题时通常要根据已知条件列出方程(组),运用方程思想求解,强化了数学运算的素养.易 错 辨 析因角度制与弧度制混用而致误【典例】 将-1 485°化成2kπ+α(0≤α<2π,k∈Z)的形式为　　　　　. 错解:因为-1 485°=-4×360°-45°=-4×360°+(-360°+315°)=-5×360°+315°,所以-1 485°化为2kπ+α(k∈Z)的形式应为-10π+315°.答案:-10π+315°以上解答过程中都有哪些错误?出错的原因是什么?你如何改正?你如何防范?提示:上述化为2kπ+α(k∈Z)的形式时错了,角度制与弧度制不能混用.正解:因为-1 485°=-5×360°+315°,防范措施 在同一式子中,两种度量制不能混用,如45°+2kπ(k∈Z)与k·360°+ (k∈Z)都是错误的表述,要么全用角度制,要么全用弧度制.