





高中数学北师大版 (2019)必修 第二册5.2 余弦函数的图象与性质再认识评课ppt课件
展开一、余弦函数的图象【问题思考】1.如何由正弦函数的图象通过图形变换得到余弦函数的图象?提示:把y=sin x,x∈R的图象向左平移 个单位长度,即可得到y=cs x,x∈R的图象.2.在确定余弦函数的图象时,哪些点是关键点?
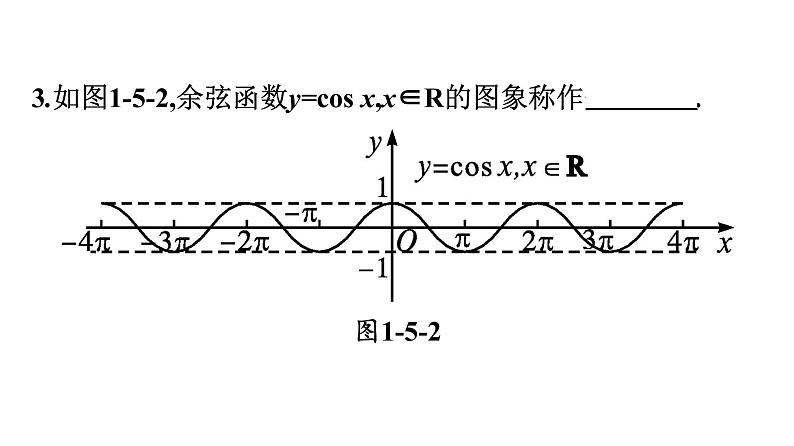
3.如图1-5-2,余弦函数y=cs x,x∈R的图象称作余弦曲线.
4.余弦函数的作图方法(1)“五点(画图)法”画余弦曲线,通常也使用“五点(画图)法”,即在函数y=cs x(x∈
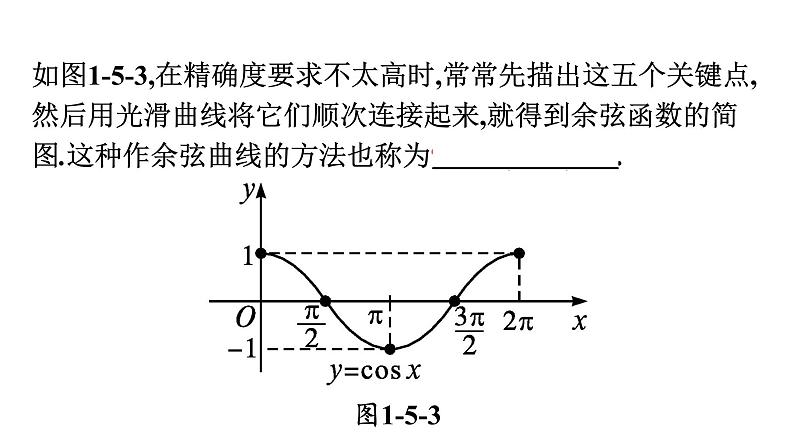
如图1-5-3,在精确度要求不太高时,常常先描出这五个关键点,然后用光滑曲线将它们顺次连接起来,就得到余弦函数的简图.这种作余弦曲线的方法也称为“五点(画图)法”.
5.(1)要得到函数y=-sin x的图象,只需将函数y=cs x的图象( ).
D.向左平移π个单位长度(2)不等式cs x<0,x∈[0,2π]的解集为 .
二、余弦函数的性质【问题思考】1.表1-5-3
2.函数y=-cs x的递减区间是( ).A.[0,π]B.[2kπ,(2k+1)π](k∈Z)C.[π,2π]D.[(2k-1)π,2kπ](k∈Z)解析:函数y=-cs x的递减区间,即函数y=cs x的递增区间,即[(2k-1)π,2kπ](k∈Z).答案:D
【例1】 用“五点(画图)法”作出函数y=2cs x-1,x∈[0,2π]的图象.分析:先在区间[0,2π]内找五个关键点,再列表、描点、连线可得函数图象.
描点、连线画图如答图1-5-3.
(1)判断函数的奇偶性;(2)求函数的单调区间;(3)求函数的最小正周期.分析:(1)根据奇偶性的定义判断;(2)根据余弦函数的单调区间求解;(3)根据余弦函数的周期定义求解.
(2)∵y=cs x在区间[2kπ-π,2kπ](k∈Z)上单调递增,在区间[2kπ,2kπ+π](k∈Z)上单调递减,
反思感悟 1.奇偶性与周期性常根据它们的定义求解,解题时注意性质的灵活运用.2.形如y=acs x+b(a≠0)函数的单调区间:(1)当a>0时,其单调性同y=cs x的单调性一致;(2)当a<0时,其单调性同y=cs x的单调性恰好相反.
【例3】 利用三角函数的单调性,比较下列各组数的大小.(1)cs 196°与cs 156°;
解:(1)cs 196°=cs(180°+16°)=-cs 16°,cs 156°=cs(180°-24°)=-cs 24°.∵0°<16°<24°<90°,且y=cs x在[0°,90°]上单调递减,∴cs 16°>cs 24°,从而-cs 16°<-cs 24°,即cs 196°
三角函数变形不等价导致奇偶性判断错误
∴f(-x)=f(x),故f(x)是偶函数.
高中数学5.2 余弦函数的图象与性质再认识备课ppt课件: 这是一份高中数学5.2 余弦函数的图象与性质再认识备课ppt课件,共27页。
高中数学北师大版 (2019)必修 第二册5.2 余弦函数的图象与性质再认识优秀ppt课件: 这是一份高中数学北师大版 (2019)必修 第二册5.2 余弦函数的图象与性质再认识优秀ppt课件,文件包含北师大版高中数学必修第二册15正弦函数余弦函数的图象与性质再认识第2课时课件pptx、北师大版高中数学必修第二册152余弦函数的图象与性质再认识同步练习含答案docx等2份课件配套教学资源,其中PPT共28页, 欢迎下载使用。
高中数学5.2 余弦函数的图象与性质再认识优秀课件ppt: 这是一份高中数学5.2 余弦函数的图象与性质再认识优秀课件ppt,文件包含北师大版高中数学必修第二册15正弦函数余弦函数的图象与性质再认识第1课时课件pptx、北师大版高中数学必修第二册151正弦函数的图象与性质再认识同步练习含答案docx等2份课件配套教学资源,其中PPT共29页, 欢迎下载使用。













