北师大版高中数学必修第二册第2章6-1第4课时正弦定理、余弦定理在实际问题中的应用课件

这是一份北师大版高中数学必修第二册第2章6-1第4课时正弦定理、余弦定理在实际问题中的应用课件，共24页。

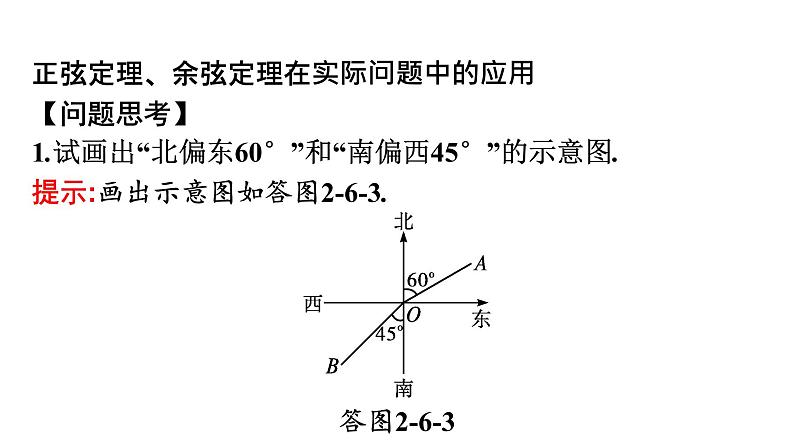
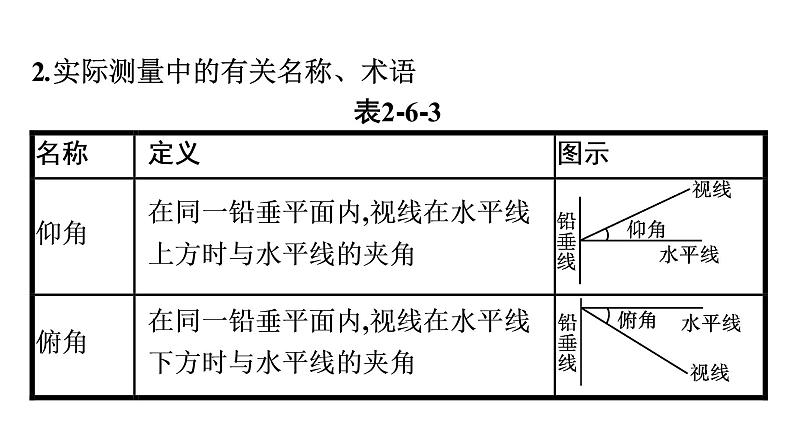
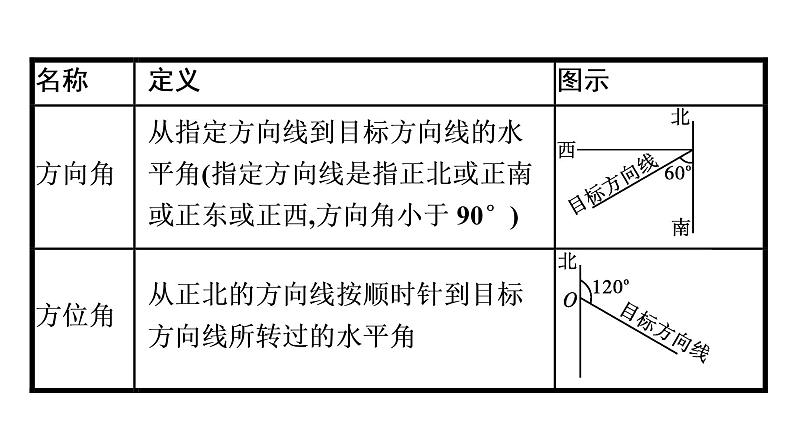
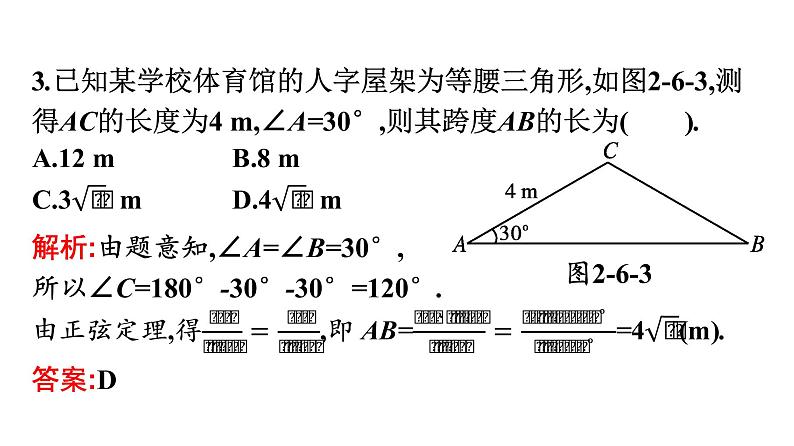
6.1　余弦定理与正弦定理第4课时　正弦定理、余弦定理在实际问题中的应用自主预习·新知导学合作探究·释疑解惑思 想 方 法 自主预习·新知导学正弦定理、余弦定理在实际问题中的应用【问题思考】1.试画出“北偏东60°”和“南偏西45°”的示意图.提示:画出示意图如答图2-6-3. 2.实际测量中的有关名称、术语表2-6-3答案:D 合作探究·释疑解惑探究一探究二探究三【例1】 如图2-6-4,隔河看到两个目标A,B,但不能到达,在岸边选取相距 km的C,D两点,并测得∠ACB=75°, ∠BCD=45°,∠ADC=30°,∠ADB=45°(A,B,C,D在同一平面内),求两个目标A,B之间的距离.分析:要求出A,B之间的距离,把AB放在△ABC(或△ADB)中,但不管在哪个三角形中,AC,BC(或AD,BD)这些量都是未知的.再把AC,BC(或AD,BD)放在△ACD和△BCD中求出它们的值.【例2】 如图2-6-6,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从点A测得点M的仰角∠MAN=60°,点C的仰角∠CAB=45°以及∠MAC=75°;从点C测得∠MCA=60°.已知山高BC=500 m,则山高MN=　　　　　 m.答案:750 反思感悟 测量高度问题的解题策略:(1)“空间”向“平面”的转化:测量高度问题往往是空间中的问题,因此先要选好所求线段所在的平面,将空间问题转化为平面问题.(2)“解直角三角形”与“解斜三角形”结合,全面分析所有三角形,仔细规划解题思路.【例3】 如图2-6-7,在海岸A处发现北偏东45°方向,距A处( -1)n mile的B处有一艘走私船.在A处北偏西75°方向,距A处2 n mile的C处的我方缉私船奉命以10 n mile/h的速度追截走私船,此时走私船正以10 n mile/h的速度,从B处向北偏东30°方向逃窜.问:缉私船应沿什么方向行驶才能最快截获走私船?并求出所需时间.∴缉私船应沿北偏东60°的方向行驶才能最快截获走私船,大约需要15分钟.反思感悟 求解实际应用中的角度问题时,一般把求角的问题转化为解三角形的问题,基本方法是:(1)明确各个角的含义;(2)分析题意,分析已知与所求,画出正确的示意图;(3)将图形中的已知量与未知量之间的关系转化为三角形的边与角的关系,运用正弦定理、余弦定理求解.思 想 方 法图2-6-8(1)求索道AB的长;(2)问:乙出发多少分钟后,乙在缆车上与甲的距离最短?分析:(1)利用正弦定理求出AB的长;(2)先设再建立时间t与甲、乙间距离d的函数解析式,利用解析式求最值.方法点睛 1.与函数思想相联系的就是方程思想.所谓方程思想,就是在解决问题时,用事先设定的未知数沟通问题所涉及的各量间的制约关系,列出方程(组),从而求出未知数及各量的值,使问题获得解决,所设的未知数沟通了变量之间的联系.方程可以看做未知量与已知量相互制约的条件,它架设了由已知探索未知的桥梁.2.函数与方程思想在数学中有着广泛的应用,本章在利用正弦定理、余弦定理求角或边长时,往往渗透着函数与方程思想.