北师大版高中数学必修第二册第4章3二倍角的三角函数公式课件

这是一份北师大版高中数学必修第二册第4章3二倍角的三角函数公式课件，共34页。
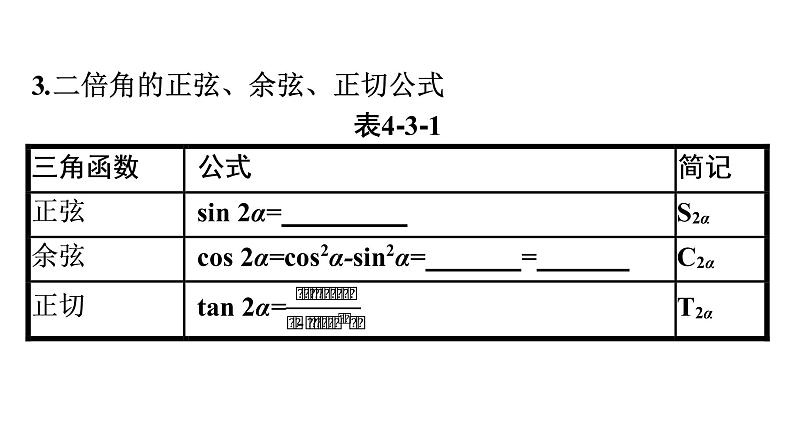
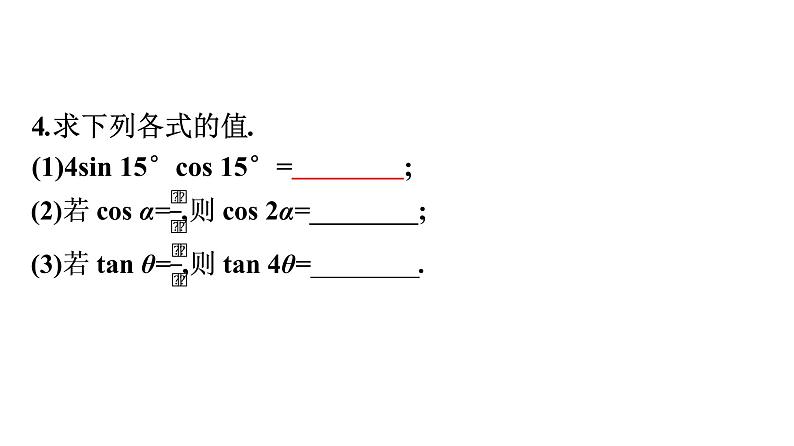
第四章　三角恒等变换§3　二倍角的三角函数公式自主预习·新知导学合作探究·释疑解惑易 错 辨 析 自主预习·新知导学一、二倍角的正弦、余弦、正切公式【问题思考】1.在两角和的正弦、余弦、正切公式中,令β=α,将得到怎样的结果?提示:sin(α+α)=sin αcos α+cos αsin α,2.cos 2α能否只用sin α或cos α表示呢?提示:根据同角三角函数关系式可得cos 2α=2cos2α-1=1-2sin2α.3.二倍角的正弦、余弦、正切公式表4-3-14.求下列各式的值.(1)4sin 15°cos 15°=　　　　; 二、二倍角公式的变形【问题思考】1.若将1±sin 2α中的“1”用sin2α+cos2α代换,那么1±sin 2α可化为什么形式?提示:1±sin 2α=sin2α±2sin αcos α+cos2α=(sin α±cos α)2.2.(1)1±sin 2α=(sin α±cos α)2; (2)升幂缩角公式:1+cos 2α=2cos2α,1-cos 2α=2sin2α;三、半角公式【问题思考】2.如何确定半角的正弦、余弦和正切公式的符号?提示:(1)若没有给出决定符号的条件,则在根号前保留正负两个符号.3.求sin 22.5°,cos 22.5°的值. 合作探究·释疑解惑探究一探究二探究三反思感悟 解决条件求值问题的方法(1)有方向地将已知式或未知式化简,使关系明朗化;寻找角之间的关系,看是否适合相关公式的使用,注意常见角的变换和角之间的二倍关系.答案:-tan 2θ 反思感悟 证明三角恒等式的原则与步骤(1)观察恒等式两端的结构形式,处理原则是从复杂到简单,高次降低,复角化单角,如果两端都比较复杂,那么将两端都化简,即采用“两头凑”的思想.(2)证明恒等式的一般步骤①先观察,找出角、函数名称、式子结构等方面的差异;②本着“复角化单角”“异名化同名”“变换式子结构”“变量集中”等原则,设法消除差异,达到证明的目的.反思感悟 三角恒等变换与三角函数图象、性质的综合问题的解题策略:运用三角函数的和、差、倍角公式将函数关系式化成y=asin ωx+bcos ωx+k的形式,借助辅助角公式化为y=Asin(ωx+φ)+k(或y=Acos(ωx+φ)+k)的形式,将ωx+φ看作一个整体研究函数的性质.易 错 辨 析因忽视角的范围致误以上解答过程中都有哪些错误?出错的原因是什么?你如何改正?你如何防范?提示:上述错解在运用二倍角公式从里到外去掉根号时,没有顾及角的范围而选择正、负号,只是机械地套用公式.