北师大版高中数学必修第二册第6章6-1柱、锥、台的侧面展开与面积课件

这是一份北师大版高中数学必修第二册第6章6-1柱、锥、台的侧面展开与面积课件，共24页。
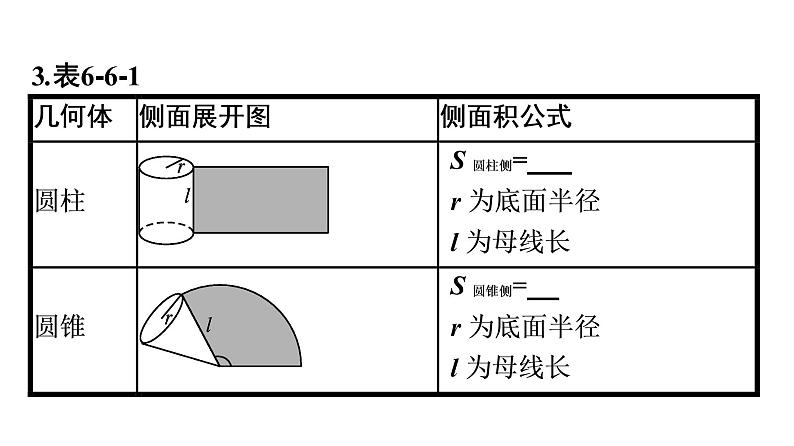
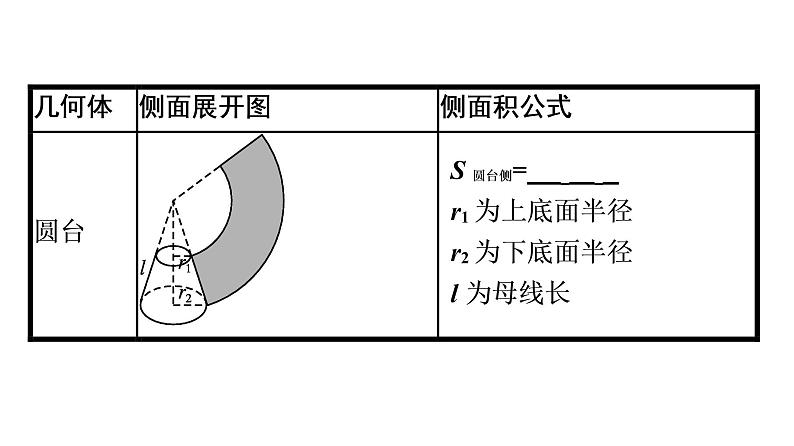
§6　简单几何体的再认识6.1　柱、锥、台的侧面展开与面积自主预习·新知导学合作探究·释疑解惑易 错 辨 析 自主预习·新知导学一、圆柱、圆锥、圆台的侧面展开及侧面积【问题思考】1.如何根据圆柱、圆锥的几何结构特征,求它们的表面积?提示:它们的表面积等于侧面积与底面积的和,利用它们的侧面展开图来求得它们的侧面积,由于底面是圆面,其底面积直接应用圆的面积公式即得.其中,圆柱的侧面展开图是矩形,圆锥的侧面展开图是扇形.2.若将一个矩形卷起,使之成为圆柱,有几种方法?得到的圆柱相同吗?侧面积相等吗?提示:有两种方法,得到的圆柱不相同,但是侧面积相等.3.表6-6-14.若一个圆锥的轴截面是等边三角形,其面积为 ,则这个圆锥的表面积是(　　).A.3π B.3 π C.6π D.9π解析:根据轴截面是等边三角形,且面积是 ,可得圆锥的母线长为2,底面半径为1,所以S=πr2+πrl=π+2π=3π.答案:A二、直棱柱、正棱锥、正棱台的侧面展开与侧面积【问题思考】1.在初中我们已经学过正方体和长方体的表面积,以及它们的展开图,你知道正方体和长方体的展开图的面积与正方体和长方体的表面积的关系吗?提示:正方体、长方体是由多个平面图形围成的多面体,它们的表面积就是围成它们的各个面的面积之和,也就是展开图的面积,如答图6-6-1.几何体表面积→展开图→平面图形面积 2.一个几何体的平面展开图一定相同吗?其表面积是否确定?提示:不同的展开方式,几何体的展开图不一定相同.表面积是各个面的面积之和,几何体的侧面展开方法可能不同,但其表面积唯一确定.3.表6-6-24.已知正四棱锥底面边长为6,侧棱长为5,则此棱锥的侧面积为(　　).A.6 B.12 C.24 D.48答案:D 合作探究·释疑解惑探究一探究二探究三【例1】 如图6-6-1,,△ABC为等腰三角形,AB=BC=2,∠ABC= 120°,将△ABC绕边BC所在的直线旋转一周,求所成几何体的表面积.在本例条件不变的前提下,若将△ABC绕边AC所在直线旋转一周,求所成几何体的表面积.解:由题意,旋转后得到的几何体是两个大小完全相同的圆锥组成的组合体,过点B向AC作垂线,垂足为H,如答图6-6-3,在Rt△ABH中,∠A=30°,从而BH= AB=1,故所求几何体的表面积S=2πrl=2π×1×2=4π.反思感悟 1.圆柱、圆锥、圆台的相关几何量都集中体现在轴截面上,因此准确把握轴截面中的相关量及其关系是求解旋转体表面积的关键.2.求几何体的表面积问题,通常将所给几何体分成基本的柱、锥、台,再通过这些柱、锥、台的表面积,进行求和或作差,从而求得几何体的表面积.【例2】 正四棱台两底面边长分别为a和b(a