北师大版 (2019)必修 第二册3.2 刻画空间点、线、面位置关系的公理导学案及答案

这是一份北师大版 (2019)必修 第二册3.2 刻画空间点、线、面位置关系的公理导学案及答案，共8页。
答案：无数个 一个 没有
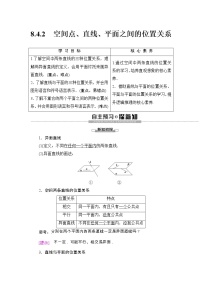
知识点2 两个平面的位置关系
答案：没有公共点 无数 α∥β α∩β＝l

研习1 直线与平面的位置关系
[典例1] (1)(多项选择题)下列说法中错误的是( )
A．若直线l上有无数个点不在平面α内，则l∥α
B．若直线l与平面α平行，则l与平面α内的任意一条直线都平行
C．如果两条平行直线中的一条与一个平面平行，那么另一条也与这个平面平行
D．若直线l与平面α平行，则l与平面α内的任意一条直线都没有公共点
(2)指出正方体ABCD－A1B1C1D1中的各个面与棱AA1所在直线的位置关系．
(1)[答案] ABC
[解析] A中，直线l也可能与α相交；
B中，l∥α，并不平行于α内的任意直线；
C中，另一条直线也有可能在平面内；
D中，直线l平行于平面α，则l与α无公共点，当然l与平面内的任意一条直线也无公共点．
(2)[解] 如图，因为A∈平面AB1，A1∈平面AB1，
所以AA1⊂平面AB1，同理AA1⊂平面AD1.
因为A∈平面AC，A1∉平面AC，
所以AA1⊄平面AC，
所以AA1∩平面AC＝A．
同理，AA1∩平面A1C1＝A1.
因为AA1⊂平面AB1，
所以AA1的所有的点都在平面AB1内．
因为平面AB1∩平面BC1＝BB1，AA1∥BB1，
所以直线AA1与BB1没有公共点．
这就是说，直线AA1与平面BC1没有公共点，即AA1∥平面BC1，同理AA1∥平面DC1.
【审题路线图】
判断直线与平面的位置关系⇒直线与平面的三种位置关系．
[延伸探究]本例(2)条件下，试分析面对角线B1D1与正方体的六个面之间的位置关系？
[自主记]
解：因为B1∈平面A1B1C1D1，D1∈平面A1B1C1D1，
所以B1D1⊂平面A1B1C1D1.
因为B1∈平面BB1C1C，D1∉平面BB1C1C，
所以直线B1D1∩平面BB1C1C＝B1.
同理直线B1D1与平面AA1B1B、平面AA1D1D、平面CC1D1D都相交．在平行四边形B1BDD1中，B1D1∥BD，所以B1D1与BD无公共点，
所以B1D1与平面ABCD无公共点，
所以B1D1∥平面ABCD.
[巧归纳] 直线与平面位置关系的判断
(1)空间直线与平面位置关系的分类是解决问题的突破口，这类判断问题，常用分类讨论的方法解决，另外，借助模型(如正方体、长方体等)也是解决这类问题的有效方法．
(2)要证明直线在平面内，只要证明直线上两点在平面α内；要证明直线与平面相交，只需说明直线与平面只有一个公共点；要证明直线与平面平行，则必须说明直线与平面没有公共点.
研习2 平面与平面位置关系的判定与应用
[典例2] (1)如果在两个平面内分别有一条直线，这两条直线互相平行，那么两个平面的位置关系一定是( )
A．平行 B．相交
C．平行或相交 D．不能确定
(2)完成下列作图．
①在图中画出两个平行平面；
②在图中画出两个相交平面；
③在图中画出一个平面与两个平行平面相交；
④在图中画出三个两两相交的平面．
(1)[答案] C
[解析] 只有一对直线平行，并不能得到两平面平行．
(2)[解] ① ②
③ ④
【审题路线图】
平面与平面的位置的判断和画法⇒两个平面的两种位置关系和画空间几何体直观图的规则．
[延伸探究]1.(变换条件)若将本例(1)条件“这两条直线互相平行”改为“这两条直线是异面直线”，则两平面的位置关系如何？
2．(变换条件)若将本例(1)条件改为“平面α内有无数条直线与平面β平行”，那么α与β的关系是什么？
3．将本例(2)改为“画出相交于一条直线的三个平面”，如何画图？
4．若本例(2)改为“试画出相交于一点的三个平面”，如何画图？
[自主记]
1．解：如图，a⊂α，b⊂β，a，b异面．
由图知，这两个平面可能平行，也可能相交．
2．解：如图，α内都有无数条直线与平面β平行．
由图知，平面α与平面β可能平行或相交．
3．解：如图所示：
4．解：如图所示(不唯一)．
[巧归纳] 1.平面与平面的位置关系的判断方法
(1)平面与平面相交的判断，主要是以公理3为依据找出一个交点．
(2)平面与平面平行的判断，主要是说明两个平面没有公共点．
2．常见的平面和平面平行的模型
(1)棱柱、棱台、圆柱、圆台的上下底面平行．
(2)长方体的六个面中，三组相对面平行．
达标篇·课堂速测演习
1．如图所示，下列用符号语言表示正确的为( )
A．α∩β＝lB．α∥β，l∈α
C．l∥β，l⊄αD．α∥β，l⊂α
答案：D
解析：面面平行：α∥β.l在α内：l⊂α.
2．在空间四边形ABCD中，E，F分别为AB，AD上的点，且AE∶EB＝AF∶FD＝1∶4，又H，G分别为BC，CD的中点，则( )
A．BD∥EF，且四边形EFGH是平行四边形
B．EF∥HG，且四边形EFGH是梯形
C．HG∥EF，且四边形EFGH是平行四边形
D．EH∥FG，且四边形EFGH是梯形
答案：B
解析：∵AE∶EB＝AF∶FD＝1∶4，
∴EF∥BD，且EF＝eq \f(1,5)BD.
又H，G分别为BC，CD的中点，
∴HG∥BD，且HG＝eq \f(1,2)BD.
∴EF∥HG，且EF≠HG，
∴四边形EFGH是梯形．故选B．
3．若直线a与平面α平行，则必有( )
A．在α内不存在与a垂直的直线
B．在α内存在与a垂直的唯一直线
C．在α内有且只有一条直线与a平行
D．在α内有无数条直线与a平行
答案：D
解析：直线a平行于平面α，则直线a与平面α内的无数条直线都平行．
4．如图，在正方体ABCD－A1B1C1D1中，判断下列位置关系：
(1)AD1所在直线与平面BCC1的位置关系是________；
(2)平面A1BC1与平面ABCD的位置关系是________．
答案：(1)平行 (2)相交
解析：(1)AD1所在的直线与平面BCC1没有公共点，所以平行；(2)平面A1BC1与平面ABCD有公共点B，故相交．
5．如图①所示，已知正方形ABCD，E，F分别是AB，CD的中点，将△ADE沿DE折起，如图②所示，则BF与ED的位置关系是________．

答案：平行
解析：∵正方形ABCD，
∴AB∥CD，且AB＝CD.
又E，F分别为AB，CD的中点，
∴BE∥FD，BE＝FD.
∴四边形BFDE为平行四边形，
∴BF∥ED.
[规范解答] 有关截面图形的问题
[示例] (12分)在正方体ABCD－A1B1C1D1中，点Q是棱DD1上的动点，判断过A，Q，B1三点的截面图形的形状．
[解题流程]

课前篇·自主学习预案
位置
关系
直线a在
平面α内
直线a在平面α外
直线a与平面α相交
直线a与平面α平行
公共点
________公共点
________公共点
________公共点
符号
表示
a⊂α
a∩α＝A
a∥α
图形
表示
位置关系
两平面平行
两平面相交
公共点
________
有________个公共点
(在一条直线上)
符号表示
________
________
图形表示
课堂篇·研习讨论导案